Имитация смеси исходных сигналов.

Смесь нормального распределния и исходного сигнала:

Данные распределения:

1,7

1,3

0,37

1,3

2,1

1,1

0,55

2,4

0,22

0,48

1,1

0,8

1,5

1,8

1,6

1,4

1,2

0,22

0,23

2,8

2,3

1,5

0,12

0,78

1,7

0,98

0,94

1,8

1,3

0,72

1,5

0,46

1,86

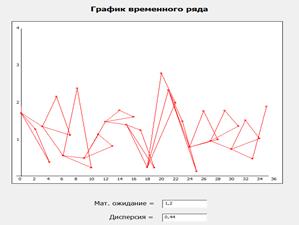
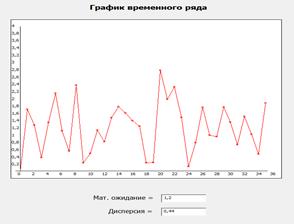
(метод построения: классический) (метод построения: исходным сигналом)

Смесь распределния Вейбула и исходного сигнала:

Данные распределения:

2,9

1,3

2,3

2,2

1,4

1,2

2,3

0,83

1,5

0,43

1,4

2,6

1,5

0,35

1,4

0,95

2,6

3,5

0,64

0,21

1,5

1,4

1,8

1,5

2,5

1,3

1,9

1,3

1,7

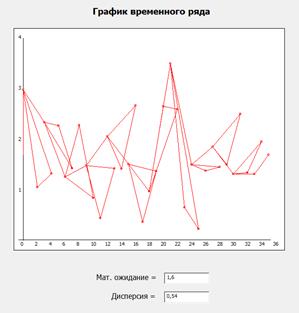
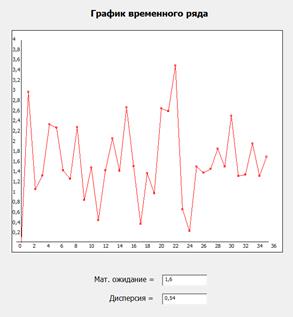
(метод построения: классический) (метод построения: исходным сигналом)

Смесь Рэлеевского распределния и исходного сигнала:

Данные распределения:

1,7

0,26

0,37

1,3

1,1

1,1

0,55

1,4

0,22

0,48

0,12

0,8

1,5

0,77

1,6

1,4

0,23

0,22

0,23

1,8

2,3

0,47

0,12

0,78

0,75

0,98

0,94

0,75

1,3

0,72

0,5

0,46

0,86

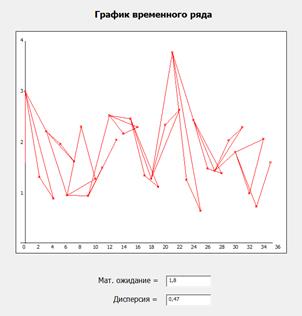
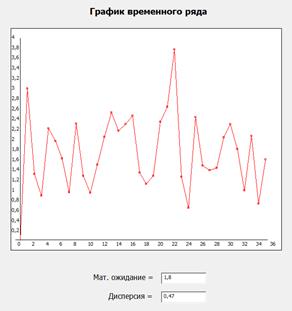
(метод построения: классический) (метод построения: исходным сигналом)

Смесь все четырех исходных сигналов:

Данные рапределения:

4,2

3,1

1,8

3,2

1,9

1,6

4,2

1,9

1,9

2,8

2,6

3,1

3,8

3,3

2,5

2,4

2,2

4,2

3,2

4,9

2,4

0,72

3,1

3,1

1,8

2,3

3,7

3,4

2,4

2,8

1,5

3,4

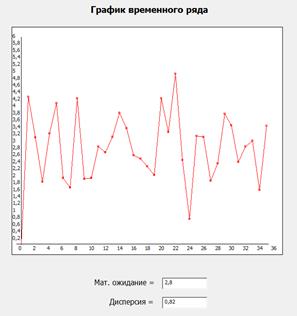
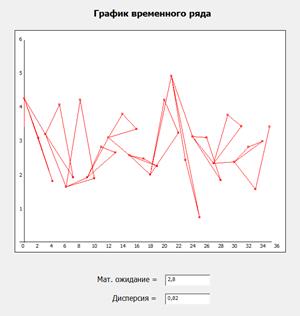
(метод построения: классический) (метод построения: исходным сигналом)

Экранные формы прогаммы:

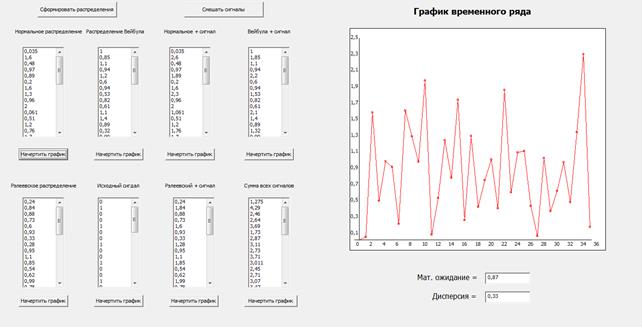
Вывод: в результате проделенной работы мыприобрели навыки построения вероятностных моделей систем. Научились моделировать случайные величина с заданным законом распределения. Проанализировали статистические характеристики имитируемых случайных процессов (шумов).

Приложение А.