Сила и плотность электрического тока
Электричество и магнетизм 2 Законы постоянного тока
3.2.1-1
На рисунке представлена зависимость плотности тока j, протекающего в проводниках 1 и 2, от напряжённости электрического поля Е.
 Отношение удельных проводимостей этих элементов σ1/σ2 равно …
Отношение удельных проводимостей этих элементов σ1/σ2 равно …
| 1: 1/2 2: 2* 3: 1/4 4: 4 |
Между плотностью тока и напряжённостью электрического поля следующая зависимость  , для модулей , для модулей  . Отсюда . Отсюда 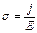 . Поэтому из графика следует . Поэтому из графика следует 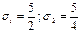 . Следовательно . Следовательно 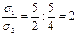 . Ответ: 2 . Ответ: 2
|
3.2.1-2
| Если увеличить в два раза напряжённость электрического поля в проводнике, то плотность тока | 1: увеличится в 2 раза* 2: увеличится в 4 раза 3: уменьшится в 2 раза 4: не изменится 5: уменьшится в 4 раза |
Плотность электрического тока связана с напряжённостью электрического поля в проводнике уравнением  , где σ – удельная электропроводность. Отсюда следует соотношение для модулей рассматриваемых величин , где σ – удельная электропроводность. Отсюда следует соотношение для модулей рассматриваемых величин  . Следовательно: при увеличении в два раза напряжённости электрического поля плотность тока увеличится в два раза. Ответ: 1 . Следовательно: при увеличении в два раза напряжённости электрического поля плотность тока увеличится в два раза. Ответ: 1
|
3.2.1-3
| Сила тока за 10 с равномерно возрастает от 1 А до 3 А. За это время через поперечное сечение проводника переносится заряд, равный … | 1: 30 Кл 2: 40 Кл 3: 10 Кл 4: 20 Кл* |
 По определению сила тока По определению сила тока  . Отсюда . Отсюда  . С геометрической точки зрения это площадь между линией функции и осью абсцисс; в данной задаче это площадь трапеции. Следовательно: . С геометрической точки зрения это площадь между линией функции и осью абсцисс; в данной задаче это площадь трапеции. Следовательно: 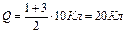 . Ответ: 4 . Ответ: 4
|
3.2.1-4
| Сила тока в проводнике в течение интервала времени t равномерно увеличивается от 0 до I, затем в течение такого же промежутка времени остается постоянной, а затем за тот же интервал времени равномерно уменьшается до нуля. За все время через проводник прошел заряд q, равный… | 1: q=It* 2: q=2It 3: 0 4: q=4It |
 Сила тока связана с электрическим зарядом соотношением Сила тока связана с электрическим зарядом соотношением 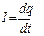 . Отсюда . Отсюда  . Исходя из геометрического смысла определённого интеграла, можно утверждать, что электрический заряд определяется площадью под кривой I(t) и осью абсцисс. В приложении к условию данного задания, заряд определится сумме площадей двух одинаковых по площади треугольников со сторонами I и t. Ясно, что искомая площадь равна . Исходя из геометрического смысла определённого интеграла, можно утверждать, что электрический заряд определяется площадью под кривой I(t) и осью абсцисс. В приложении к условию данного задания, заряд определится сумме площадей двух одинаковых по площади треугольников со сторонами I и t. Ясно, что искомая площадь равна  . Ответ: 1 . Ответ: 1
|
3.2.1-5