Инженерно-технический институт
Литература
1. Угай Я.А. Общая и неорганическая химия. М.: Высш. шк., 1997.
2. Ахметов Н.С. Общая и неорганическая химия. М.: Высш. шк., 1998.
3. Коровин Н.В. Общая химия. М.: Высш. шк., 1998.
4. Гольбрайх З.Е., Маслов Е.И. Сборник задач и упражнений по химии. М.: Высш. шк., 1997.
5. Лидин Р.А., Молочко В.А., Андреева Л.Л. Задачи по неорганической химии. М.: Высш. шк., 1990.
6. Романцева Л.М., Лещинская З.Л., Суханова В.А. Сборник задач и упражнений по общей химии. М.: Высш. шк., 1991.
7. Витинг Л.М., Резницкий Л.А. Задачи и упражнения по общей химии. М.: Изд-во МГУ, 1995.
| образованные двумя или несколькими веществами. Жидкие растворы состоят из жидкого растворителя (обычно Н2О) и одного или нескольких растворенных веществ, которые до смешения с растворителем могли быть твердыми, жидкими или газообразными.
Количественный состав раствора принято выражать через безразмерные относительные величины (иначе доли: массовую, объемную, молярную) или через размерные величины – концентрации. В табл. 1 приведены формулы для расчета наиболее часто применяемых способов выражения состава растворов (индекс «1» обозначает характеристику растворителя, индекс «2» относится к растворенному веществу, а отсутствие индекса указывает на свойство раствора как целого).
Таблица 1
Основные способы выражения состава раствора
| | Способ выражения состава раствора
| Формула
| | | Массовая доля растворенного вещества (процентная концентрация по массе) w – отношение массы растворенного вещества к массе раствора, доли единицы или % мас.
|
w = m2/ m =
= m2/ (m1 + m2)
| | | Молярная (мольная) доля компонента раствора N i – отношение количества вещества данного компонента к общему количеству вещества, находящегося в растворе, доли единицы или % мол.
| N1= n1 / (n1 + n2);
N2 = n2 / (n1 + n2);
N1 + N2 = 1
| | | Объемная доля j – отношение объема компонента раствора к объему раствора, доли единицы или % объем.
| j = V2 / V
| | | Моляльная концентрация (моляльность) b – отношение количества растворенного вещества к массе растворителя, моль/кг
| b = n2 / m1 =
= m2 /(M2 × m1)
| | | Молярная концентрация (молярность) СМ – отношение количества растворенного вещества к объему раствора, моль/дм3 или М
| СМ= n2 /V =
= m2 /(M2 × V )
| | Молярная концентрация эквивалентов вещества (нормальность) СН – отношение количества эквивалентов растворенного вещества к объему раствора, моль/дм3 или н.
| СН= n2 [1/ z] / V =
= m2 / ( M2 [1/ z] × V )
| | | Титр раствора Т показывает массу растворенного вещества, содержащегося в 1 см3 раствора, г/см3
| Т = m2 /V
| | | | | | | | Пример 1.Массовая доля вещества.
Определить массовую долю (в % мас.) хлорида калия, в 750 см3 раствора которого содержится 79,7г KCl, плотность раствора 1,063 г/см3.
| | | |
| | | | | |
| | | | | | |
| | Р е ш е н и е
w =  = =  = =  = 10 % мас.
Пример 2.Упаривание раствора.
При упаривании 50 г раствора с массовой долей соли w1 = 0,2 масса раствора уменьшилась на D m = 10 г. Определить массовую долю соли в растворе w2 после упаривания.
Р е ш е н и е
1. w1= m2/ m, следовательно, m2 =w1× m;
2. w2 = = 10 % мас.
Пример 2.Упаривание раствора.
При упаривании 50 г раствора с массовой долей соли w1 = 0,2 масса раствора уменьшилась на D m = 10 г. Определить массовую долю соли в растворе w2 после упаривания.
Р е ш е н и е
1. w1= m2/ m, следовательно, m2 =w1× m;
2. w2 =   = =  = =  = 0,25.
Пример 3.Разбавление раствора.
Определить объем 50%-ного раствора азотной кислоты (в см3) плотностью 1,315 г/см3, необходимого для приготовления 5 дм3 2%-ного раствора, плотность которого 1,010 г/см3.
Р е ш е н и е
1. Примем обозначения для величин, указанных в условии задачи:
для раствора 1: w1= 50 % = 0,5; r1 = 1,315 г/см3; V1 – ?;
для раствора 2: w2= 2 % = 0,02; r2 = 1,010 г/см3; V2 = 5 дм3.
2. w1 = m1/( r1 × V1), следовательно, V1 = m1/(r1× w1);
w2 = m2/(r2 × V2), следовательно, m2 = V2 × r2× w2.
Раствор 2 получают, прибавляя к раствору 1 воду, поэтому m1 = m2. Тогда в формулу для V1 следует подставить выражение для m2.
3. V1 = = 0,25.
Пример 3.Разбавление раствора.
Определить объем 50%-ного раствора азотной кислоты (в см3) плотностью 1,315 г/см3, необходимого для приготовления 5 дм3 2%-ного раствора, плотность которого 1,010 г/см3.
Р е ш е н и е
1. Примем обозначения для величин, указанных в условии задачи:
для раствора 1: w1= 50 % = 0,5; r1 = 1,315 г/см3; V1 – ?;
для раствора 2: w2= 2 % = 0,02; r2 = 1,010 г/см3; V2 = 5 дм3.
2. w1 = m1/( r1 × V1), следовательно, V1 = m1/(r1× w1);
w2 = m2/(r2 × V2), следовательно, m2 = V2 × r2× w2.
Раствор 2 получают, прибавляя к раствору 1 воду, поэтому m1 = m2. Тогда в формулу для V1 следует подставить выражение для m2.
3. V1 = 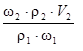 = =  = 18,7 см3.
Общее правило, используемое для приготовления разбавленных растворов из концентрированных: при одном и том же количестве растворенного вещества массы растворов и их массовые доли обратно = 18,7 см3.
Общее правило, используемое для приготовления разбавленных растворов из концентрированных: при одном и том же количестве растворенного вещества массы растворов и их массовые доли обратно | |
| | |  |
| |
| | | |
| | | | | | | | |
| | |
| 705,2
|
| 1817,2
|
| 4242,2
| |
| 757,3
|
| 1937,1
|
| 4753,0
| |
| 813,3
|
| 2065,1
|
| 5318,0
| |
| 871,9
|
| 2197,1
|
| 5940,0
| |
| 934,6
|
| 2338,4
|
| 6623,0
| |
| 1001,2
|
| 2486,4
|
| 7374,0
| |
| 1073,2
|
| 2643,7
|
| 12334,0
| |
| 1147,8
|
| 2809,1
|
| 19920,0
| |
| 1227,9
|
| 2983,7
|
| 31160,0
| |
| 1311,9
|
| 3167,7
|
| 43360,0
| |
| 1402,5
|
| 3361,0
|
| 70100,0
| |
| 1497,2
|
| 3565,0
|
| 101325,0
| Таблица 2
Криоскопические (K) и эбулиоскопические (Е) константы некоторых растворителей
| Растворитель
| К
| Е
| Растворитель
| К
| Е
| | Вода
| 1,86
| 0,52
| Этиловый спирт
| --
| 1,16
| | Бензол
| 5,10
| 2,57
| Ацетон
| 2,40
| 1,50
| | Анилин
| 5,87
| 3,69
| Хлороформ
| 4,90
| 3,89
|
Таблица 3
Константы диссоциации слабых электролитов при 25 °С
| Электролит
| Уравнение диссоциации
| Кдис
| | Азотистая кислота
| HNO2 Û H+ + NO2-
| 4,0×10-4
| |
Борная кислота
| H3BO3 Û H+ + H2BO3-
H2BO3- Û H+ + HBO32-
HBO32- Û H+ + BO33-
| 6,0×10-10
1,8×10-13
1,6×10-14
| | Вода
| H2O Û H+ + OH-
| 1,8×10-16
| | | | | | пропорциональны друг другу:
w1 × m1 = w2 × m2 или 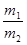 = =  . .  Пример 4.Концентрирование раствора.
Какую массу сухой соли (х) нужно добавить к 50 г раствора с массовой долей этой же соли w1 = 0,1, чтобы получить раствор, массовая доля соли в котором равна w2 = 0,2.
Р е ш е н и е
1. w1= m2 / m, следовательно, m2 = w1 × m, где m2 – масса соли в исходном растворе. Тогда
w2 =
Пример 4.Концентрирование раствора.
Какую массу сухой соли (х) нужно добавить к 50 г раствора с массовой долей этой же соли w1 = 0,1, чтобы получить раствор, массовая доля соли в котором равна w2 = 0,2.
Р е ш е н и е
1. w1= m2 / m, следовательно, m2 = w1 × m, где m2 – масса соли в исходном растворе. Тогда
w2 =  , или w2 = , или w2 =  .
2. Решаем полученное уравнение относительно х:
w2× m + w2× х = w1× m + х ;
w2× m –w1× m = х –w2× х ;
(w2 – w1)× m = (1 – w2)× х ;
х = .
2. Решаем полученное уравнение относительно х:
w2× m + w2× х = w1× m + х ;
w2× m –w1× m = х –w2× х ;
(w2 – w1)× m = (1 – w2)× х ;
х =  = =  = 5,56г.
Пример 5.Смешивание растворов с разными концентрациями.
Смешали два раствора: массой m1 с массовой долей растворенного вещества w1 и массой m2 с массовой долей того же вещества w2, причем w1 > w2. Образовался раствор, массовая доля растворенного вещества в котором равна w3. Выразите соотношение m1 / m2.
Р е ш е н и е
1. Пусть w1× m1– масса растворенного вещества в первом растворе; w2× m2- масса растворенного вещества во втором растворе; (m1+ m2)– масса образовавшегося раствора; w3× (m1 + m2)– масса растворенного вещества в образовавшемся растворе. Сумма масс растворенного вещества в первом и втором растворах равна массе этого вещества в образовавшемся растворе:
w1× m1 + w2× m2 = w3×(m1 + m2);
w1× m1 – w3× m1 = w3× m2 - w2× m2; = 5,56г.
Пример 5.Смешивание растворов с разными концентрациями.
Смешали два раствора: массой m1 с массовой долей растворенного вещества w1 и массой m2 с массовой долей того же вещества w2, причем w1 > w2. Образовался раствор, массовая доля растворенного вещества в котором равна w3. Выразите соотношение m1 / m2.
Р е ш е н и е
1. Пусть w1× m1– масса растворенного вещества в первом растворе; w2× m2- масса растворенного вещества во втором растворе; (m1+ m2)– масса образовавшегося раствора; w3× (m1 + m2)– масса растворенного вещества в образовавшемся растворе. Сумма масс растворенного вещества в первом и втором растворах равна массе этого вещества в образовавшемся растворе:
w1× m1 + w2× m2 = w3×(m1 + m2);
w1× m1 – w3× m1 = w3× m2 - w2× m2;
| |
| |
| | | | | |
| | | | | | | | |
| |  | | 24. Вычислить рН 1 М раствора сульфата цинка, гидролизующегося по первой ступени.
25. При смешении растворов Al(НSO4)3 и K2S в осадок выпадает Al(OH)3. Указать причину этого и составить соответствующие молекулярные и ионно-молекулярные уравнения.
ПРИЛОЖЕНИЕ
Таблица 1
Давление насыщенного водяного пара при различных температурах
| °C
| Р, Па
| °С
| Р, Па
| °С
| Р, Па
| |
| 610,4
|
| 1598,5
|
| 3780,0
| |
| 657,2
|
| 1705,2
|
| 4005,0
| | | | |
| |
| | | | | |
| | | | | | | | |
| | | а) NaBr; б) NaClO4; в) NaCN. Написать сокращенные ионные уравнения, указать рН среды.
4. Написать сокращенное ионное уравнение и вычислить константу и степень гидролиза 0,05 М раствора СН3СООNa.
5. Написать уравнение гидролиза в сокращенном ионном виде и указать рН среды для солей: а) CuCl2; б) Ca(CH3COO)2; в) Pb(NO3)2.
6. Написать уравнение гидролиза в сокращенном ионном виде и вычислить константу и степень гидролиза 0,2 М раствора Na2CO3 по первой ступени.
7. Указать, какую реакцию среды будут иметь растворы приведенных солей, подтвердив это соответствующими уравнениями гидролиза: а) NaNO2; б) CoCl2; в) Ba(NO2)2.
8. Написать уравнение гидролиза в сокращенном ионном виде и вычислить степени гидролиза по катиону и аниону в 0,3 М растворе (NH4)2S.
9. Указать, какие из приведенных солей будут подвергаться гидролизу, написать сокращенные ионные уравнения, указать рН среды: а) K2CO3; б) (NH4)2SO4; в) CsNO3.
10. Рассчитать константу и степень гидролиза в 0,1 М растворе фосфата натрия по первой ступени.
11. Написать уравнение гидролиза в сокращенном ионном виде и указать рН среды для солей: а) NaHS; б) (NH4)2S; в) K2SO4.
12. Вычислить константу гидролиза и степень гидролиза сульфита натрия в 0,1 М растворе.
13. Указать, какую реакцию среды будут иметь растворы следующих солей, подтвердив это соответствующими уравнениями гидролиза: а) NH4NO3; б) Mg(CH3COO)2; в) SnCl2.
14. Написать молекулярно-ионные формы уравнений гидролиза (отдельно для катиона и аниона) и указать рН среды для солей: а) Na3AsO4; б) CoSO4; в) AlCl3.
15. Рассчитать константу и степень гидролиза гипохлорита калия в 0,1 М растворе соли.
16. Написать уравнение гидролиза в сокращенном ионном виде и указать рН среды для солей: а) KH2PO4; б) Pb2S; в) KNO2.
17. Написать уравнения гидролиза и указать реакцию среды растворов следующих солей: а) Ba(HCOO)2; б) Al(CH3COO)3; в) Mn(ClO4)2 .
18. Написать уравнения гидролиза в сокращенном ионном виде и указать рН среды для солей: а) ZnCl2; б) Na2HPO4; в) Ca(HS)2 .
19. Написать уравнения гидролиза и указать реакцию среды растворов следующих солей: а) ZnSO4; б) NaHS; в) CrI3 .
20. Написать уравнение гидролиза в сокращенном ионном виде и указать рН среды для солей: а) СuSO4; б) Fe(НSO3)2; в) KHCО3 .
21. Указать, какие из приведенных солей будут подвергаться гидролизу, написать сокращенные ионные уравнения, указать рН среды: а) K2CO3; б) Ca(CH3COO)2; в) AlCl3.
22. Написать уравнения гидролиза и указать реакцию среды растворов следующих солей: а) NH4NO3; б) Al(CH3COO)3; в) ZnCl2.
23. Вычислить степень гидролиза и рН в 0,1 М растворе NaHS.
| | | СМ =  = =  = =  = 0,693 моль/дм3;
СН = = 0,693 моль/дм3;
СН =  = =  = =  = 1,386 моль/дм3.
3. Получим соотношение между молярными концентрациями: = 1,386 моль/дм3.
3. Получим соотношение между молярными концентрациями:  М2[1 / z] =
М2[1 / z] =  , тогда СН = , тогда СН =  × 2 = 2 × СМ.
4. Общее правило пересчета молярных концентраций: молярная концентрация эквивалентов вещества в z раз больше молярной концентрации растворенного вещества, т. е. СН = z× СМ, где z – основность кислоты (кислотность основания) или для соли – произведение числа атомов металла на его степень окисления.
Пример 8.Приготовление растворов.
Вычислить объем раствора серной кислоты с массовой долей 96 % мас. (r = 1840 г/дм3), необходимого для приготовления раствора объемом 2 дм3 с молярной концентрацией 0,25 моль/дм3.
Р е ш е н и е
1. w = × 2 = 2 × СМ.
4. Общее правило пересчета молярных концентраций: молярная концентрация эквивалентов вещества в z раз больше молярной концентрации растворенного вещества, т. е. СН = z× СМ, где z – основность кислоты (кислотность основания) или для соли – произведение числа атомов металла на его степень окисления.
Пример 8.Приготовление растворов.
Вычислить объем раствора серной кислоты с массовой долей 96 % мас. (r = 1840 г/дм3), необходимого для приготовления раствора объемом 2 дм3 с молярной концентрацией 0,25 моль/дм3.
Р е ш е н и е
1. w =  ×100 % ,
где Vx – объем раствора серной кислоты, который нужно разбавить водой для приготовления нового раствора. Отсюда
Vx = ×100 % ,
где Vx – объем раствора серной кислоты, который нужно разбавить водой для приготовления нового раствора. Отсюда
Vx = 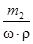 ×100 % .
2. Массу H2SO4 можно получить из формулы для молярной концентрации:
m2 = CМ× M2× V.
3. Формула для расчета Vx будет иметь вид
Vx = ×100 % .
2. Массу H2SO4 можно получить из формулы для молярной концентрации:
m2 = CМ× M2× V.
3. Формула для расчета Vx будет иметь вид
Vx =  ×100 % ×100 %  ×100 % = ×100 % =
| |
| |
| | | | | |
| | | | | | | | |
| | | = 0,028 дм3.
З А Д А Ч И
1. Вычислить молярную и нормальную концентрации 49 %-ного раствора ортофосфорной кислоты (r = 1,33 г/см3).
2. Вычислить процентное содержание серной кислоты в ее 5 М растворе (r = = 1,29 г/см3).
3. Сколько литров 0,1 н. раствора нитрата серебра необходимо для реакции с 0,5 дм3 0,3 н. раствора AlCl3?
4. Определить массовую долю (% мас.) хлорида натрия в растворе, полученном при смешении 20 %-ного раствора хлорида натрия массой 20 г и 30 %-ного раствора поваренной соли объемом 100 см3 и плотностью 1,09 г/см3.
5. Сколько соли нужно растворить в воде массой 2 кг, чтобы получить раствор с массовой долей 0,2?
6. Определить молярную концентрацию раствора, полученного при разбавлении 2 М раствора объемом 200 см3 водой объемом 300 см3?
7. Определить, какая масса ортофосфорной кислоты содержится в растворе объемом 0,5 дм3, если концентрация кислоты равна 0,3 н.
8. Чему равна нормальная концентрация 50 %-ного раствора серной кислоты (r = 1,4 г/см3 )?
9. Сколько граммов соли и воды содержится в 800 г 12 %-ного раствора нитрата натрия?
10. Требуется приготовить раствор массой 500 г с массовой долей хлорида калия 14 % мас. Рассчитать массы требуемых хлорида калия и воды.
11. Чему равна молярная концентрация 20 %-ного раствора HСl, плотность которого составляет 1,10 г/см3?
12. Вычислить молярность и нормальность 40 %-ного раствора H3PO4 (r = = 1,25 г/см3).
13. Чему равна нормальная концентрация 18 %-ного раствора серной кислоты (r = 1,29 г/см3)?
14. Чему равна массовая процентная концентрация H2SO4 в ее 10 н. растворе (r = 1,29 г/см3)?
15. На нейтрализацию 50 см3 раствора щелочи израсходовано 30 см3 0,2 н. раствора серной кислоты. Какова нормальность раствора щелочи? Сколько 0,1 н. раствора HСl потребовалось бы для этой же цели?
16. Определить молярную долю дийода в неводном растворе, полученном смешиванием 5,02 г дийода и 100,04 г этанола.
17. Рассчитать моляльность неводного раствора хлорида ртути (II), полученного смешиванием 9,98 г растворенного вещества и 120 см3 этанола плотностью 785 г/дм3.
18. Определить массу растворенного вещества (в г), содержащегося в 200 см3 0,075 н. раствора сульфата рубидия.
| | | Na3BO3 + HOH Û Na2НBO3 + NaOH, рН > 7.
Пример 2.В какую сторону сместится гидролитическое равновесие при смешивании растворов карбоната натрия и сульфата алюминия?
Р е ш е н и е
Al2(SO4)3 + 3Na2CO3 + 6HOH ® 2Al(OH)3¯ + 3H2O + 3CO2 + 3Na2SO4 .
В результате смешивания растворов катионы Н+, образующиеся при гидролизе Al2(SO4)3, соединяются с анионами ОН–, образующимися при гидролизе Na2CO3, что приводит к смещению равновесия реакции в сторону образования продуктов гидролиза. Смещение усиливается за счет разложения образующихся молекул Н2CO3 и выделения малорастворимого основания Al(OH)3, поэтому реакция идет практически до конца. В ионной форме уравнение реакции имеет вид
2Al3+ + 3CO + 6HOH ® 2Al(OH)3¯ + 3H2O + 3CO2
Пример 3.Вычислить константу гидролиза, степень гидролиза и рН 0,02 М раствора СН3СООK.
Р е ш е н и е
Соль СН3СООKобразована сильным основанием КОНи слабой кислотой СН3СООН. Ионное уравнение гидролиза:
СН3СОО– + НОН Û СН3СООН + ОН– .
Kг =  = =  = 5,56×10-10;
h = = 5,56×10-10;
h =  = =  = 1,67×10-4;
[ОН–] = h× СМ = 1,67×10-4×0,02 = 3,34×10-6; рОН = –lg 3,34×10-6 = 5,48;
рН = 14 – рОН = 14 – 5,48 = 8,52.
З А Д А Ч И
1. Вычислить константу и степень гидролиза KCN в 0,1 М растворе.
2. Написать уравнение гидролиза в сокращенном ионном виде и указать рН среды для солей: а) NaClO; б) (NH4)2SO4; в) СH3COOK.
3. Указать, какие из приведенных солей будут подвергаться гидролизу: = 1,67×10-4;
[ОН–] = h× СМ = 1,67×10-4×0,02 = 3,34×10-6; рОН = –lg 3,34×10-6 = 5,48;
рН = 14 – рОН = 14 – 5,48 = 8,52.
З А Д А Ч И
1. Вычислить константу и степень гидролиза KCN в 0,1 М растворе.
2. Написать уравнение гидролиза в сокращенном ионном виде и указать рН среды для солей: а) NaClO; б) (NH4)2SO4; в) СH3COOK.
3. Указать, какие из приведенных солей будут подвергаться гидролизу: | |
| |
| | | | | |
| | | | | | | | |
| | [H+] = 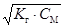 ; [H+] = h × СМ; рН = -lg[H+] = -lg ; [H+] = h × СМ; рН = -lg[H+] = -lg 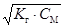 .
3) гидролиз по катиону и аниону одновременно:
Kг = .
3) гидролиз по катиону и аниону одновременно:
Kг =  , ,  = =  .
Для этого случая концентрация раствора соли практически не влияет на h:
h = .
Для этого случая концентрация раствора соли практически не влияет на h:
h = 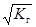 .
Кроме того, [H+] = .
Кроме того, [H+] =  ; рН = -lg ; рН = -lg  .
Согласно принципу Ле Шателье:
1) чем слабее кислота или основание, образующиеся при гидролизе соли, тем сильнее эта соль гидролизуется;
2) разбавление раствора соли усиливает гидролиз;
3) гидролиз по катиону (аниону) усиливается при добавлении к раствору соли основания (кислоты);
4) при повышении температуры гидролиз усиливается.
Пример 1.Определить рН водного раствора бората натрия.
Р е ш е н и е
Na3BO3 + HOH Û H3BO3 + NaOH .
Гидролиз соли, образованной сильным основанием NaOHи слабой многоосновной кислотой H3BO3 определяется ступенчатым характером диссоциации борной кислоты и обратного процесса – соединения ионов BO .
Согласно принципу Ле Шателье:
1) чем слабее кислота или основание, образующиеся при гидролизе соли, тем сильнее эта соль гидролизуется;
2) разбавление раствора соли усиливает гидролиз;
3) гидролиз по катиону (аниону) усиливается при добавлении к раствору соли основания (кислоты);
4) при повышении температуры гидролиз усиливается.
Пример 1.Определить рН водного раствора бората натрия.
Р е ш е н и е
Na3BO3 + HOH Û H3BO3 + NaOH .
Гидролиз соли, образованной сильным основанием NaOHи слабой многоосновной кислотой H3BO3 определяется ступенчатым характером диссоциации борной кислоты и обратного процесса – соединения ионов BO  с ионами Н+.
Процесс гидролиза бората натрия можно выразить уравнениями:
I ступень: ВO с ионами Н+.
Процесс гидролиза бората натрия можно выразить уравнениями:
I ступень: ВO  + HOH Û HВO + HOH Û HВO  + OH– ;
II ступень: НВO + OH– ;
II ступень: НВO  + HOH Û H2ВO + HOH Û H2ВO  + OH– ;
III ступень: H2ВO + OH– ;
III ступень: H2ВO  + НOH Û H3BO3 + OH– .
Как правило, гидролиз заканчивается на I ступени. Тогда молекулярное уравнение гидролиза имеет вид: + НOH Û H3BO3 + OH– .
Как правило, гидролиз заканчивается на I ступени. Тогда молекулярное уравнение гидролиза имеет вид:
| | | 19. Следующая реакция проводится смешиванием водных растворов реагентов:
ZnCl2 + 4NaOH = Na2[Zn(OH)4] + 2NaCl.
Определить эквивалентную концентрацию первого реагента в 200 см3 исходного раствора, если в нем содержалось 1,83 г этого вещества.
20. В 800 г воды растворили оксид серы (IV) объемом 7,84 л (н.у.). Вычислить массовую долю оксида в полученном растворе.
21. Найти массовое процентное содержание AgNO3 в растворе, если эквивалентная концентрация его равна 0,64 моль/дм3 (r = 1088 г/ дм3).
22. Найти массовую процентную концентрацию KМnO4, если нормальная концентрация соли составляет 0,4 н. (r = 1,04 г/см3).
23. Определить объем раствора серной кислоты с массовой долей 0,093 и плотностью раствора 1,05 г/см3, который потребуется для приготовления 0,35 М раствора серной кислоты объемом 40 см3.
24. К 2 М раствору KCl объемом 40 см3 (r = 1,09 г/см3) добавили 200 г воды. Определить молярную концентрацию полученного раствора и массовую долю хлорида калия в нем. Плотность полученного раствора равна 1,015 г/см3.
25. Рассчитать титр 0,04 н. раствора хлорида натрия.
СВОЙСТВА РАЗБАВЛЕННЫХ РАСТВОРОВ НЕЭЛЕКТРОЛИТОВ
1. Осмотическое давление
Осмосомназывают явление односторонней диффузии молекул растворителя через полупроницаемую перегородку, разделяющую растворы с различным содержанием растворенного вещества. Давление, которое нужно приложить к раствору, чтобы остановить одностороннюю диффузию растворителя, называют осмотическим.
Связь между осмотическим давлением и составом разбавленных растворов неэлектролитов, Па или кПа, описывается законом Вант-Гоффа:
росм = 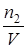 R T = С R T или росм = СМ R T ,
где С – концентрация, моль/м3; СМ– концентрация, моль/дм3; R – универсальная газовая постоянная, Дж/(моль×К); T – абсолютная температура, К.
Уравнение позволяет вычислить для разбавленных растворов неэлектролитов:
1) молекулярную массу растворенного вещества;
2) концентрацию раствора;
3) осмотическое давление раствора. R T = С R T или росм = СМ R T ,
где С – концентрация, моль/м3; СМ– концентрация, моль/дм3; R – универсальная газовая постоянная, Дж/(моль×К); T – абсолютная температура, К.
Уравнение позволяет вычислить для разбавленных растворов неэлектролитов:
1) молекулярную массу растворенного вещества;
2) концентрацию раствора;
3) осмотическое давление раствора.
| |
| |
| | | | | |
| | | | | | | | |
| | Растворы, обладающие одинаковым осмотическим давлением, называются изотоническими.
Пример 1.В 250 см3 раствора содержится 17 мг растворенного вещества. Осмотическое давление раствора при 27 °С равно 1,84 кПа. Вычислить молярную массу растворенного вещества.
Р е ш е н и е
По закону Вант-Гоффа росм V = n2 R T =  R T . Тогда формула для расчета молярной массы растворенного вещества имеет вид
М2 = R T . Тогда формула для расчета молярной массы растворенного вещества имеет вид
М2 = 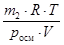 = = 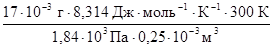 = 92 г/моль.
Пример 2.Вычислить осмотическое давление раствора при 22 °С, в 1,2 дм3 которого содержится 0,021 г сахара С12Н22О11.
Р е ш е н и е
1. Молярная концентрация раствора составит
СМ = = 92 г/моль.
Пример 2.Вычислить осмотическое давление раствора при 22 °С, в 1,2 дм3 которого содержится 0,021 г сахара С12Н22О11.
Р е ш е н и е
1. Молярная концентрация раствора составит
СМ =  = =  = 5×10-5 моль/дм3.
2. росм = СМ R T = 5×10-5 моль/дм3 × 8,314 Дж / (моль × К) × 295 К = 0,13 кПа.
Пример 3.Определить массу глюкозы С6Н12О6 , которую должен содержать 1 дм3 раствора, чтобы быть изотоничным раствору, содержащему в 1 дм3 9,2 г глицерина С3Н8О3.
Р е ш е н и е
1. Определим молярную концентрацию глицерина
СМ(С3Н8О3) = = 5×10-5 моль/дм3.
2. росм = СМ R T = 5×10-5 моль/дм3 × 8,314 Дж / (моль × К) × 295 К = 0,13 кПа.
Пример 3.Определить массу глюкозы С6Н12О6 , которую должен содержать 1 дм3 раствора, чтобы быть изотоничным раствору, содержащему в 1 дм3 9,2 г глицерина С3Н8О3.
Р е ш е н и е
1. Определим молярную концентрацию глицерина
СМ(С3Н8О3) =  = = 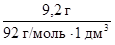 = 0,1 моль/дм3.
2. При одинаковой температуре изотоническими будут растворы с одинаковой молярной концентрацией неэлектролита. Следовательно, масса глюкозы будет равна = 0,1 моль/дм3.
2. При одинаковой температуре изотоническими будут растворы с одинаковой молярной концентрацией неэлектролита. Следовательно, масса глюкозы будет равна
| | | NH4COOH + HOH Û NH4OH + HCOOH, рН = 7,
так как Kдис(HCOOH) = Kдис(NH4OH) = 1,76 × 10-5.
4. Необратимый полный гидролиз.
Если кислота и основание, образующие соль, являются не только слабыми электролитами, но и малорастворимы или неустойчивы и разлагаются с образованием газообразных продуктов, то гидролиз, как правило, протекает практически необратимо, например:
Al2S3 + 6HOH ® 2Al(OH)3¯ + 3H2S ;
2Al3+ + 3S2– + 6HOH ® 2Al(OH)3¯ + 3H2S .
Количественно гидролиз соли характеризуется степенью гидролиза h и константой гидролиза Kг.
Степень гидролиза h показывает,какая часть соли находится в гидролизованном состоянии и выражается в долях единицы или в процентах:
h = Сг/ Собщ,
где Сг – концентрация гидролизованной части соли; Собщ– общая концентрация растворенной соли.
Расчет константы гидролиза Kг и степени гидролиза h ведут по формулам:
1) гидролиз по аниону:
Kг =  , h = , h =  = =  ,
где Kк-ты – константа диссоциации слабой кислоты.
Изменение рН раствора соли, происходящее в результате ее гидролиза, может быть вычислено по формуле:
Kг = ,
где Kк-ты – константа диссоциации слабой кислоты.
Изменение рН раствора соли, происходящее в результате ее гидролиза, может быть вычислено по формуле:
Kг =  ; [ОН –] = ; [ОН –] = 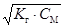 и [ОН –] = h× СМ ;
рН = 14 – рОН = 14 + lg и [ОН –] = h× СМ ;
рН = 14 – рОН = 14 + lg 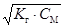 2) гидролиз по катиону:
Kг =
2) гидролиз по катиону:
Kг = 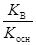 , h = , h =  = =  ,
где Kосн – константа диссоциации слабого основания. ,
где Kосн – константа диссоциации слабого основания.
| |
| |
| | | | | |
| | | | | | | | |
| | СН3СООNa ® СН3СОО – + Na+;
Na+ + HOH®реакция практически не идет;
СН3СОО – + HOH Û СН3СООН + ОН –,рН > 7.
Молекулярное уравнение гидролиза
СН3СООNa + HOH Û СН3СООН + NaОН .
Если анион многозарядный, то в числе продуктов могут быть кислые соли, например:
Na2CO3 + HOH Û NaHCO3 + NaOH;
I ступень гидролиза: CO  + HOH Û HCO + HOH Û HCO  + OH –;
II ступень гидролиза: НCO + OH –;
II ступень гидролиза: НCO  + HOH Û H2CO3 + NaOH .
Накапливающиеся в растворе ионы ОН –препятствуют протеканию II ступени гидролиза, поэтому чаще всего гидролиз идет только по I ступени.
2.Гидролиз по катиону.
Соли слабого основания и сильной кислоты гидролизуются с увеличением концентрации катионов водорода в растворе, т. е. реакция среды кислая (рН < 7), например:
(NH4)2SO4 ® 2NH4+ + SO + HOH Û H2CO3 + NaOH .
Накапливающиеся в растворе ионы ОН –препятствуют протеканию II ступени гидролиза, поэтому чаще всего гидролиз идет только по I ступени.
2.Гидролиз по катиону.
Соли слабого основания и сильной кислоты гидролизуются с увеличением концентрации катионов водорода в растворе, т. е. реакция среды кислая (рН < 7), например:
(NH4)2SO4 ® 2NH4+ + SO  ;
SO ;
SO  + HOH ® реакция практически не идет;
NH4+ + HOH Û NH4OH + H+, рН < 7.
Молекулярное уравнение гидролиза:
(NH4)2SO4 + HOH Û NH4OH + NH4HSO4 .
При этом гидролиз не доходит до конца, так как накопление в растворе ионов водорода препятствует образованию свободной кислоты.
3. Гидролиз по катиону и аниону одновременно.
В реакции участвуют и катион, и анион соли. Реакция среды определяется относительной силой образующихся слабой кислоты и слабого основания. Если Kдис (кисл) > Kдис (осн), то рН < 7; если Kдис (кисл) < Kдис (осн), то рН > 7, а когда Kдис(кисл) = Kдис (осн), то рН » 7.
Например: + HOH ® реакция практически не идет;
NH4+ + HOH Û NH4OH + H+, рН < 7.
Молекулярное уравнение гидролиза:
(NH4)2SO4 + HOH Û NH4OH + NH4HSO4 .
При этом гидролиз не доходит до конца, так как накопление в растворе ионов водорода препятствует образованию свободной кислоты.
3. Гидролиз по катиону и аниону одновременно.
В реакции участвуют и катион, и анион соли. Реакция среды определяется относительной силой образующихся слабой кислоты и слабого основания. Если Kдис (кисл) > Kдис (осн), то рН < 7; если Kдис (кисл) < Kдис (осн), то рН > 7, а когда Kдис(кисл) = Kдис (осн), то рН » 7.
Например:
| | | m(С6Н12О6) = СМ(С3Н8О3) × M(С6Н12О6) × V,
m(С6Н12О6) = 0,1 моль/дм3 × 180 г/моль × 1 дм3 = 18 г.
2. Давление пара. I закон Рауля
Пар над жидкостью в состоянии равновесия называется насыщенным. Давление насыщенного пара – характерная величина для данного вещества и зависит от температуры. При постоянной температуре давление пара раствора р всегда ниже давления пара чистого растворителя р 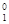 . Связь между р и р . Связь между р и р 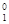 в случае нелетучего растворенного вещества устанавливает I закон Рауля: относительное понижение давления пара растворителя над разбавленным раствором неэлектролита Dр /p в случае нелетучего растворенного вещества устанавливает I закон Рауля: относительное понижение давления пара растворителя над разбавленным раствором неэлектролита Dр /p 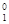 пропорционально мольной доле растворенного вещества N2: пропорционально мольной доле растворенного вещества N2:
 = = 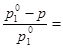 N2 . N2 .  Так как в разбавленных растворах n2 << n1, то при расчете мольной доли допустимо считать, что N2 = n2 /n1, тогда закон Рауля примет вид
Так как в разбавленных растворах n2 << n1, то при расчете мольной доли допустимо считать, что N2 = n2 /n1, тогда закон Рауля примет вид
 .
Значения давления насыщенного водяного пара при различных температурах приведены в табл. 1 приложения.
Пример 1.Вычислить давление пара воды над раствором, содержащим 45 г глюкозы С6Н12О6 в 720 г воды при 25 °С.
Р е ш е н и е
Давление пара воды при 25 °С составляет р .
Значения давления насыщенного водяного пара при различных температурах приведены в табл. 1 приложения.
Пример 1.Вычислить давление пара воды над раствором, содержащим 45 г глюкозы С6Н12О6 в 720 г воды при 25 °С.
Р е ш е н и е
Давление пара воды при 25 °С составляет р 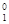 = 3168 Па (см. табл. 1 приложения). По I закону Рауля
р = р = 3168 Па (см. табл. 1 приложения). По I закону Рауля
р = р 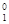 – р – р  × × 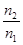 = р = р 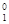 – р – р 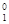 × ×  ,
р = 3168 – 3168× ,
р = 3168 – 3168×  = 3148,2 Па . = 3148,2 Па .
| |
| |
| | | | | |
| | | | | | | | |
| | Пример 2.Вычислить молярную массу неэлектролита, если 28,5 г этого вещества, растворенного в 785 г воды, вызывают понижение давления пара воды над раствором на 52,37 Па при 40 °С.
Р е ш е н и е
Давление пара воды при 40 °С составляет 7375,9 Па (см. табл. 1). По I закону Рауля
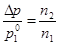 = =  , ,  ,
отсюда М2 = 92,04 г/моль.
3. Температура кипения и замерзания. II закон Рауля
Согласно II закону Рауля, повышение температуры кипения DTкип и понижение температуры замерзания DTзам раствора по сравнению с чистым растворителем прямо пропорционально моляльной концентрации растворенного вещества – неэлектролита:
DTкип = Tкип – Т ,
отсюда М2 = 92,04 г/моль.
3. Температура кипения и замерзания. II закон Рауля
Согласно II закону Рауля, повышение температуры кипения DTкип и понижение температуры замерзания DTзам раствора по сравнению с чистым растворителем прямо пропорционально моляльной концентрации растворенного вещества – неэлектролита:
DTкип = Tкип – Т  = E × b;DTзам = Tзам – Т = E × b;DTзам = Tзам – Т  = K × b,
где Ткип , Т = K × b,
где Ткип , Т  – температура кипения раствора и чистого растворителя, К; Тзам, Т – температура кипения раствора и чистого растворителя, К; Тзам, Т  – температура замерзания раствора и чистого растворителя, К; b ‑ моляльность раствора, моль/кг; E, K – эбулиоскопическая и криоскопическая константы, кг×К/моль.
Таким образом, раствор кипит при более высокой температуре, чем чистый растворитель, а замерзает при более низкой температуре.
Значения E и K некоторых растворителей приведены в табл. 2.
Молярную массу растворенного вещества по повышению температуры кипения или понижению температуры замерзания раствора вычисляют по формулам:
M2 = E × – температура замерзания раствора и чистого растворителя, К; b ‑ моляльность раствора, моль/кг; E, K – эбулиоскопическая и криоскопическая константы, кг×К/моль.
Таким образом, раствор кипит при более высокой температуре, чем чистый растворитель, а замерзает при более низкой температуре.
Значения E и K некоторых растворителей приведены в табл. 2.
Молярную массу растворенного вещества по повышению температуры кипения или понижению температуры замерзания раствора вычисляют по формулам:
M2 = E ×  ; M2 = K × ; M2 = K ×  .
Пример.Определить температуру кипения и температуру замерзания раствора, содержащего 1 г нитробензола С6Н5NO2 в 10 г бензола. Температура кипения чистого бензола 80,2 °С, температура замерзания чистого бензола 5,4 °С.
Р е ш е н и е .
Пример.Определить температуру кипения и температуру замерзания раствора, содержащего 1 г нитробензола С6Н5NO2 в 10 г бензола. Температура кипения чистого бензола 80,2 °С, температура замерзания чистого бензола 5,4 °С.
Р е ш е н и е
| | | | 15. ПР(Са3(РО4)2) = 1×10-25 при 25 °С. Рассчитать концентрацию ионов Са2+ и РО43- в насыщенном растворе при этой же температуре.
16. Насыщенный при комнатной температуре раствор PbSO4 объемом 3 дм3 содержит 0,132 г соли. Вычислить ПР(PbSO4).
17. При 18 °С ПР(PbF2) составляет 3,2×10-8. Какое количество свинца содержится в 0,4 дм3 насыщенного раствора?
18. Насыщенный раствор AgIO3 объемом 3 дм3 содержит в виде ионов 0,176 г серебра. Вычислить ПР(AgIO3).
19. Раствор содержит ионы Ва2+ и Sr2+, концентрации которых соответственно равны 5×10-4 и 5×10-1 моль/дм3. Какой из осадков будет первым выпадать в растворе при постепенном прибавлении раствора K2CrO4? ПР(SrCrO4) = = 3,6×10-5.
20. ПР(Ag3PO4) составляет 1,8×10-18. В каком объеме насыщенного раствора содержится 0,05 г растворенной соли?
21. Выпадет ли осадок сульфата кальция, если к 0,1 дм3 0,01 М раствора Ca(NO3)2 прибавить 0,4 дм3 0,001 н. раствора H2SO4? Степень диссоциации Ca(NO3)2 и H2SO4 равна 95 %; ПР(CaSO4) = 6,1×10-5.
22. Рассчитать ПР(Ni(NO3)2), если массовая доля Ni(NO3)2 в насыщенном растворе при некоторой температуре равна 0,205 % (плотность раствора принять равной 1 г/см3).
23. Рассчитать, какой объем воды (в дм3) потребуется для растворения 0,0158 г SrCO3 при 25 °С, если ПР(SrCO3) = 5,3×10-10 (объем воды принять равным объему раствора).
24. Рассчитать равновесную молярную концентрацию (моль/дм3) катионов в насыщенном растворе солей AgMoO4 (ПР = 2,8×10-12) и TlC2O4 (ПР = 2,0×10-4) при 25 °С.
25. Рассчитать равновесную молярную концентрацию анионов в насыщенном растворе солей BaF2 (ПР = 1,7×10-6) и Ca(IO3)2 (ПР = 1,9×10-6) при 25 °С.
ГИДРОЛИЗ СОЛЕЙ
Гидролизом солиназываетсявзаимодействие ионов соли с молекулами воды, сопровождающееся изменением рН раствора.
Гидролиз протекает только тогда, когда при взаимодействии ионов и воды образуются малодиссоциированные вещества (слабые кислоты или основания, а также комплексные ионы). Соли, образованные сильным основанием и сильной кислотой, гидролизу не подвергаются.
Возможны следующие случаи гидролиза солей.
1. Гидролиз по аниону.
Соли сильного основания и слабой кислоты гидролизуются с увеличением концентрации гидроксид-ионов в растворе, т. е. реакция среды щелочная (рН > 7), например:
| |
| |
| | | | | |
| | | | | | | | |
| | исходных растворов в порядке их перечисления в условии задачи; (V1+ V2) – объем конечного раствора.
При смешивании равных объемов начальных растворов концентрации ионов в конечном растворе уменьшаются в 2 раза по сравнению с с1и с2.
[Pb2+]×[I–]2 =   = =  = = 7,4×10-8 .
PbI2осаждается, так как соблюдается условие выпадения осадка:
7,4×10-8 >8,7×10-9.
З А Д А Ч И
1. Растворимость AgI равна 1,2×10-8 моль/дм3. Вычислить ПР(AgI).
2. В 2 дм3 воды при 25 °С растворяется 2,2×10-4 г бромида серебра. Вычислить ПР(AgBr).
3. Произведение растворимости PbCl2 равно 1,7×10-5. Чему равна концентрация ионов свинца в насыщенном растворе PbCl2?
4. Произведение растворимости CaSO4 равно 6×10-5. Выпадает ли осадок CaSO4, если смешать равные объемы 0,2 н. растворов CaCl2 и Na2CO3?
5. ПР (PbI2) = 8,7×10-5. Выпадет ли осадок, если смешать равные объемы растворов, содержащих 3 г/дм3 Pb(NO3)2 и 1 г/дм3 KI?
6. Произведение растворимости AgCl равно 1,6×10-10. Вычислить концентрацию насыщенного раствора AgCl (в моль/дм3 и в г/дм3).
7. Сколько воды потребуется для растворения 1 г СаС2О4 при комнатной температуре, если ПР(СаС2О4) = 2,6×10-9?
8. Сколько граммов СаСО3 может раствориться в 1 дм3 воды при 18 °С, если ПР(СаСО3) = 4,8×10-9 при той же температуре?
9. Вычислить концентрацию ионов Ag+ в насыщенном растворе AgBr, содержащем NaBr концентрации 0,01 моль/дм3.
10. Рассчитать значение ПР, если растворимость вещества Ме2А в воде при некоторой температуре равна 1,2×10-3 моль/дм3.
11. Рассчитать значение ПР гидроксида металла Ме(ОН)2, если рН его насыщенного раствора равен 9,54 при 25 °С.
12. Рассчитать ПР(PbSO4), если массовая доля PbSO4 в насыщенном растворе при некоторой температуре равна 0,057 % (плотность раствора принять равной 1 г/см3).
13. Определить, выпадет ли осадок после сливания равных объемов 0,0023 М растворов AgNO3 и KBr при 25 °С.
14. Определить, выпадет ли осадок после сливания 5 см3 0,004 М раствора CdCl2 и 15 см3 0,003 М раствора NaOH при 25 °С. = = 7,4×10-8 .
PbI2осаждается, так как соблюдается условие выпадения осадка:
7,4×10-8 >8,7×10-9.
З А Д А Ч И
1. Растворимость AgI равна 1,2×10-8 моль/дм3. Вычислить ПР(AgI).
2. В 2 дм3 воды при 25 °С растворяется 2,2×10-4 г бромида серебра. Вычислить ПР(AgBr).
3. Произведение растворимости PbCl2 равно 1,7×10-5. Чему равна концентрация ионов свинца в насыщенном растворе PbCl2?
4. Произведение растворимости CaSO4 равно 6×10-5. Выпадает ли осадок CaSO4, если смешать равные объемы 0,2 н. растворов CaCl2 и Na2CO3?
5. ПР (PbI2) = 8,7×10-5. Выпадет ли осадок, если смешать равные объемы растворов, содержащих 3 г/дм3 Pb(NO3)2 и 1 г/дм3 KI?
6. Произведение растворимости AgCl равно 1,6×10-10. Вычислить концентрацию насыщенного раствора AgCl (в моль/дм3 и в г/дм3).
7. Сколько воды потребуется для растворения 1 г СаС2О4 при комнатной температуре, если ПР(СаС2О4) = 2,6×10-9?
8. Сколько граммов СаСО3 может раствориться в 1 дм3 воды при 18 °С, если ПР(СаСО3) = 4,8×10-9 при той же температуре?
9. Вычислить концентрацию ионов Ag+ в насыщенном растворе AgBr, содержащем NaBr концентрации 0,01 моль/дм3.
10. Рассчитать значение ПР, если растворимость вещества Ме2А в воде при некоторой температуре равна 1,2×10-3 моль/дм3.
11. Рассчитать значение ПР гидроксида металла Ме(ОН)2, если рН его насыщенного раствора равен 9,54 при 25 °С.
12. Рассчитать ПР(PbSO4), если массовая доля PbSO4 в насыщенном растворе при некоторой температуре равна 0,057 % (плотность раствора принять равной 1 г/см3).
13. Определить, выпадет ли осадок после сливания равных объемов 0,0023 М растворов AgNO3 и KBr при 25 °С.
14. Определить, выпадет ли осадок после сливания 5 см3 0,004 М раствора CdCl2 и 15 см3 0,003 М раствора NaOH при 25 °С.
| | | 1. Используя табл. 2, определим эбулиоскопическую и криоскопическую константы бензола: Е = 2,57 кг×К/моль; K = 5,1 кг×К/моль.
2. По II закону Рауля повышение температуры кипения раствора нитробензола в бензоле определяется по формуле
DTкип = E ×  = 2,57 кг × К/моль× = 2,57 кг × К/моль×  2,09 К.
3. Температура кипения раствора равна
Ткип= DTкип+ Т 2,09 К.
3. Температура кипения раствора равна
Ткип= DTкип+ Т  = 2,09 + 80,2 = 82,29 °С.
4. По закону Рауля понижение температуры замерзания раствора нитробензола в бензоле составит
DTзам = K × = 2,09 + 80,2 = 82,29 °С.
4. По закону Рауля понижение температуры замерзания раствора нитробензола в бензоле составит
DTзам = K ×  = 5,1 кг×К/моль × = 5,1 кг×К/моль ×  4,14 К .
5. Температура замерзания раствора равна
Тзам= Т 4,14 К .
5. Температура замерзания раствора равна
Тзам= Т  –DTзам= 5,4 – 4,14 = 1,26 °С.
З А Д А Ч И
1. При какой температуре осмотическое давление раствора, содержащего 45 г глюкозы в 1 дм3, достигнет 607,8 кПа?
2. Раствор, 1 см3 которого содержит 0,0405 г некоторого растворенного вещества, изотоничен с 0,225 М раствором сахара. Вычислить молекулярную массу растворенного вещества.
3. Вычислить давление пара раствора, в 450 г которого содержится 90 г глюкозы при 25 °С.
4. При 0 °С давление пара эфира (С2Н5)2О составляет 2465 Па. Найти для этой температуры давление пара 5 %-ного раствора анилина С6Н5NH2 в эфире.
5. Сколько граммов сахара содержится в 250 см3 раствора, осмотическое давление которого при 7 °С составляет 283,6 кПа? Вычислить молярность раствора. В каком объеме (см3) раствора содержится 1 моль сахара?
6. Вычислить давление пара 10 %-ного раствора сахара при 100 °С.
7. Сколько граммов глюкозы С6Н12О6 следует растворить в 260 г воды для получения раствора, температура кипения которого превышает температуру кипения чистого растворителя на 0,05°?
8. Температура кипения ацетона равна 56,1 °С (E = 1,73). Вычислить температуру кипения 8 %-ного раствора глицерина С3Н6О3 в ацетоне.
9. Вычислить осмотическое давление 25 %-ного раствора сахара при 15 °С (r = 1,105 г/см3). –DTзам= 5,4 – 4,14 = 1,26 °С.
З А Д А Ч И
1. При какой температуре осмотическое давление раствора, содержащего 45 г глюкозы в 1 дм3, достигнет 607,8 кПа?
2. Раствор, 1 см3 которого содержит 0,0405 г некоторого растворенного вещества, изотоничен с 0,225 М раствором сахара. Вычислить молекулярную массу растворенного вещества.
3. Вычислить давление пара раствора, в 450 г которого содержится 90 г глюкозы при 25 °С.
4. При 0 °С давление пара эфира (С2Н5)2О составляет 2465 Па. Найти для этой температуры давление пара 5 %-ного раствора анилина С6Н5NH2 в эфире.
5. Сколько граммов сахара содержится в 250 см3 раствора, осмотическое давление которого при 7 °С составляет 283,6 кПа? Вычислить молярность раствора. В каком объеме (см3) раствора содержится 1 моль сахара?
6. Вычислить давление пара 10 %-ного раствора сахара при 100 °С.
7. Сколько граммов глюкозы С6Н12О6 следует растворить в 260 г воды для получения раствора, температура кипения которого превышает температуру кипения чистого растворителя на 0,05°?
8. Температура кипения ацетона равна 56,1 °С (E = 1,73). Вычислить температуру кипения 8 %-ного раствора глицерина С3Н6О3 в ацетоне.
9. Вычислить осмотическое давление 25 %-ного раствора сахара при 15 °С (r = 1,105 г/см3).
| |
| |
| | | | | |
| | | | | | | | |
| | | 10. Сколько граммов сахара С12Н22О11 следует растворить в 720 г воды для получения раствора, давление пара которого на 18,66 Па ниже давления пара Н2О при 20 °С?
11. Вычислить, на сколько градусов понизится температура замерзания бензола С6Н6, если в 50 г его растворить 1,5 г нафталина С10Н8.
12. Осмотическое давление раствора при –3 °С составляет 2735 кПа. При какой температуре осмотическое давление достигнет 3040 кПа?
13. При растворении 0,4 г некоторого вещества в 10 г воды температура кристаллизации раствора понижается на 1,24°. Вычислить молекулярную массу растворенного вещества.
14. Вычислить давление пара раствора, в 468 г которого содержится 18 г глюкозы С6Н12О6 при 25 °С.
15. Вычислить осмотическое давление 4 %-ного раствора сахара при 20 °С, если плотность раствора равна 1,014 г/см3.
16. Вычислить давление пара раствора при 65 °С, содержащего 13,68 г сахара в 90 г Н2О, если давление водяного пара при той же температуре равно 24 994 Па.
17. На сколько градусов понизится давление пара при температуре 28 °С, если в 340 г воды растворить 54 г глюкозы.
18. Вычислить, при какой температуре осмотическое давление раствора, содержащего 45 г глюкозы в 1 дм3, достигнет 656,8 кПа.
19. Раствор сахара в воде показывает повышение температуры кипения на 0,312°. Вычислить величину понижения температуры замерзания этого раствора.
20. Осмотическое давление раствора, в 0,25 дм3 которого содержится 0,66 г мочевины, равно 111439 Па при 33 °С. Вычислить молекулярную массу мочевины.
21. Найти молекулярную массу неэлектролита, если при растворении 12 г его в 292 г Н2О при 10 °С понижение давления пара раствора составило 28,4 Па.
22. Температура замерзания бензола С6Н6 равна 5,5 °С. Раствор, содержащий 6,15 г нитробензола в 400 г бензола, замерзает при 4,86 °С. Вычислить молекулярную массу нитробензола.
23. Сколько молекул растворенного вещества содержится в 1 см3 раствора, осмотическое давление которого при 54 °С составляет 6 065 Па?
24. Давление пара раствора, содержащего в 270 г воды 12 г неэлектролита при 70 °С, равно 30 749,6 Па. Вычислить молекулярную массу растворенного вещества.
25. Определить молекулярную массу эфира, если при 30 °С давление пара раствора, содержащего 3,08 г анилина в 370 г эфира, равно 85 792 Па, а давление пара растворителя при той же температуре составляет 86 365 Па.
СВОЙСТВА РАСТВОРОВ ЭЛЕКТРОЛИТОВ
| | | MgF2(тв) Û Mg2+ + 2F –
ПР(MgF2) = [Mg2+] [ F –]2 = L ×(2L)2 = 4 L3 = 4 × (0,001)3 = 4 × 10-9.
Пример 2.Рассчитать равновесную молярную концентрацию (моль/дм3) анионов в насыщенном растворе карбоната серебра (I) при 25 °С, если ПР = 8,7×10-12.
Р е ш е н и е
Ag2CO3(тв) Û2Ag+ + CO32-;
ПР(Ag2CO3) = [Ag+]2 × [CO32- ] = (2 × [CO32- ])2 × [CO32- ] = 4 × [CO32- ]3;
[CO32- ] =  1,3×10-4 моль/дм3.
Пример 3.Определить рН насыщенного раствора гидроксида кальция при 25 °С, если ПР = 6,3×10-6.
Решение
Са(ОН)2(тв)Û Са2+ + 2ОН– ;
рН = [Са2+] × [ОН–]2 = 1/2×[ОН–] × [ОН–]2 = 1/2×[ОН–]3;
рН = 14 – рОН = 14 + lg[ОН–] = 14 + lg 1,3×10-4 моль/дм3.
Пример 3.Определить рН насыщенного раствора гидроксида кальция при 25 °С, если ПР = 6,3×10-6.
Решение
Са(ОН)2(тв)Û Са2+ + 2ОН– ;
рН = [Са2+] × [ОН–]2 = 1/2×[ОН–] × [ОН–]2 = 1/2×[ОН–]3;
рН = 14 – рОН = 14 + lg[ОН–] = 14 + lg  = 14 + lg = 14 + lg  = 12,4.
Пример 4.Выпадет ли осадок иодида свинца (II) при 25 °С после сливания 100 см3 0,005 М раствора нитрата свинца (II) и 200 см3 0,01 М раствора иодида калия, если ПР (PbI2) = 8,7×10-9?
Решение
Pb(NO3)2 + 2KI = PbI2(тв)+ 2KNO3;
Pb2+ + 2I– = PbI2(тв);
[Pb2+] = = 12,4.
Пример 4.Выпадет ли осадок иодида свинца (II) при 25 °С после сливания 100 см3 0,005 М раствора нитрата свинца (II) и 200 см3 0,01 М раствора иодида калия, если ПР (PbI2) = 8,7×10-9?
Решение
Pb(NO3)2 + 2KI = PbI2(тв)+ 2KNO3;
Pb2+ + 2I– = PbI2(тв);
[Pb2+] =  ; [I –] = ; [I –] =  ,
где с1и с2 – концентрации ионов в растворах до смешивания; V1и V2 – объемы ,
где с1и с2 – концентрации ионов в растворах до смешивания; V1и V2 – объемы | |
| |
| | | | | |


 =
=  =
=  = 10 % мас.
Пример 2.Упаривание раствора.
При упаривании 50 г раствора с массовой долей соли w1 = 0,2 масса раствора уменьшилась на D m = 10 г. Определить массовую долю соли в растворе w2 после упаривания.
Р е ш е н и е
1. w1= m2/ m, следовательно, m2 =w1× m;
2. w2 =
= 10 % мас.
Пример 2.Упаривание раствора.
При упаривании 50 г раствора с массовой долей соли w1 = 0,2 масса раствора уменьшилась на D m = 10 г. Определить массовую долю соли в растворе w2 после упаривания.
Р е ш е н и е
1. w1= m2/ m, следовательно, m2 =w1× m;
2. w2 = 
 =
=  =
=  = 0,25.
Пример 3.Разбавление раствора.
Определить объем 50%-ного раствора азотной кислоты (в см3) плотностью 1,315 г/см3, необходимого для приготовления 5 дм3 2%-ного раствора, плотность которого 1,010 г/см3.
Р е ш е н и е
1. Примем обозначения для величин, указанных в условии задачи:
для раствора 1: w1= 50 % = 0,5; r1 = 1,315 г/см3; V1 – ?;
для раствора 2: w2= 2 % = 0,02; r2 = 1,010 г/см3; V2 = 5 дм3.
2. w1 = m1/( r1 × V1), следовательно, V1 = m1/(r1× w1);
w2 = m2/(r2 × V2), следовательно, m2 = V2 × r2× w2.
Раствор 2 получают, прибавляя к раствору 1 воду, поэтому m1 = m2. Тогда в формулу для V1 следует подставить выражение для m2.
3. V1 =
= 0,25.
Пример 3.Разбавление раствора.
Определить объем 50%-ного раствора азотной кислоты (в см3) плотностью 1,315 г/см3, необходимого для приготовления 5 дм3 2%-ного раствора, плотность которого 1,010 г/см3.
Р е ш е н и е
1. Примем обозначения для величин, указанных в условии задачи:
для раствора 1: w1= 50 % = 0,5; r1 = 1,315 г/см3; V1 – ?;
для раствора 2: w2= 2 % = 0,02; r2 = 1,010 г/см3; V2 = 5 дм3.
2. w1 = m1/( r1 × V1), следовательно, V1 = m1/(r1× w1);
w2 = m2/(r2 × V2), следовательно, m2 = V2 × r2× w2.
Раствор 2 получают, прибавляя к раствору 1 воду, поэтому m1 = m2. Тогда в формулу для V1 следует подставить выражение для m2.
3. V1 = 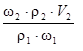 =
=  = 18,7 см3.
Общее правило, используемое для приготовления разбавленных растворов из концентрированных: при одном и том же количестве растворенного вещества массы растворов и их массовые доли обратно
= 18,7 см3.
Общее правило, используемое для приготовления разбавленных растворов из концентрированных: при одном и том же количестве растворенного вещества массы растворов и их массовые доли обратно 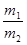 =
=  .
.  , или w2 =
, или w2 =  .
2. Решаем полученное уравнение относительно х:
w2× m + w2× х = w1× m + х ;
w2× m –w1× m = х –w2× х ;
(w2 – w1)× m = (1 – w2)× х ;
х =
.
2. Решаем полученное уравнение относительно х:
w2× m + w2× х = w1× m + х ;
w2× m –w1× m = х –w2× х ;
(w2 – w1)× m = (1 – w2)× х ;
х =  =
=  = 5,56г.
Пример 5.Смешивание растворов с разными концентрациями.
Смешали два раствора: массой m1 с массовой долей растворенного вещества w1 и массой m2 с массовой долей того же вещества w2, причем w1 > w2. Образовался раствор, массовая доля растворенного вещества в котором равна w3. Выразите соотношение m1 / m2.
Р е ш е н и е
1. Пусть w1× m1– масса растворенного вещества в первом растворе; w2× m2- масса растворенного вещества во втором растворе; (m1+ m2)– масса образовавшегося раствора; w3× (m1 + m2)– масса растворенного вещества в образовавшемся растворе. Сумма масс растворенного вещества в первом и втором растворах равна массе этого вещества в образовавшемся растворе:
w1× m1 + w2× m2 = w3×(m1 + m2);
w1× m1 – w3× m1 = w3× m2 - w2× m2;
= 5,56г.
Пример 5.Смешивание растворов с разными концентрациями.
Смешали два раствора: массой m1 с массовой долей растворенного вещества w1 и массой m2 с массовой долей того же вещества w2, причем w1 > w2. Образовался раствор, массовая доля растворенного вещества в котором равна w3. Выразите соотношение m1 / m2.
Р е ш е н и е
1. Пусть w1× m1– масса растворенного вещества в первом растворе; w2× m2- масса растворенного вещества во втором растворе; (m1+ m2)– масса образовавшегося раствора; w3× (m1 + m2)– масса растворенного вещества в образовавшемся растворе. Сумма масс растворенного вещества в первом и втором растворах равна массе этого вещества в образовавшемся растворе:
w1× m1 + w2× m2 = w3×(m1 + m2);
w1× m1 – w3× m1 = w3× m2 - w2× m2;
 =
=  =
=  = 0,693 моль/дм3;
СН =
= 0,693 моль/дм3;
СН =  =
=  =
=  = 1,386 моль/дм3.
3. Получим соотношение между молярными концентрациями:
= 1,386 моль/дм3.
3. Получим соотношение между молярными концентрациями:  , тогда СН =
, тогда СН =  × 2 = 2 × СМ.
4. Общее правило пересчета молярных концентраций: молярная концентрация эквивалентов вещества в z раз больше молярной концентрации растворенного вещества, т. е. СН = z× СМ, где z – основность кислоты (кислотность основания) или для соли – произведение числа атомов металла на его степень окисления.
Пример 8.Приготовление растворов.
Вычислить объем раствора серной кислоты с массовой долей 96 % мас. (r = 1840 г/дм3), необходимого для приготовления раствора объемом 2 дм3 с молярной концентрацией 0,25 моль/дм3.
Р е ш е н и е
1. w =
× 2 = 2 × СМ.
4. Общее правило пересчета молярных концентраций: молярная концентрация эквивалентов вещества в z раз больше молярной концентрации растворенного вещества, т. е. СН = z× СМ, где z – основность кислоты (кислотность основания) или для соли – произведение числа атомов металла на его степень окисления.
Пример 8.Приготовление растворов.
Вычислить объем раствора серной кислоты с массовой долей 96 % мас. (r = 1840 г/дм3), необходимого для приготовления раствора объемом 2 дм3 с молярной концентрацией 0,25 моль/дм3.
Р е ш е н и е
1. w =  ×100 % ,
где Vx – объем раствора серной кислоты, который нужно разбавить водой для приготовления нового раствора. Отсюда
Vx =
×100 % ,
где Vx – объем раствора серной кислоты, который нужно разбавить водой для приготовления нового раствора. Отсюда
Vx = 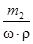 ×100 % .
2. Массу H2SO4 можно получить из формулы для молярной концентрации:
m2 = CМ× M2× V.
3. Формула для расчета Vx будет иметь вид
Vx =
×100 % .
2. Массу H2SO4 можно получить из формулы для молярной концентрации:
m2 = CМ× M2× V.
3. Формула для расчета Vx будет иметь вид
Vx =  ×100 %
×100 %  ×100 % =
×100 % =
 =
=  = 5,56×10-10;
h =
= 5,56×10-10;
h =  =
=  = 1,67×10-4;
[ОН–] = h× СМ = 1,67×10-4×0,02 = 3,34×10-6; рОН = –lg 3,34×10-6 = 5,48;
рН = 14 – рОН = 14 – 5,48 = 8,52.
З А Д А Ч И
1. Вычислить константу и степень гидролиза KCN в 0,1 М растворе.
2. Написать уравнение гидролиза в сокращенном ионном виде и указать рН среды для солей: а) NaClO; б) (NH4)2SO4; в) СH3COOK.
3. Указать, какие из приведенных солей будут подвергаться гидролизу:
= 1,67×10-4;
[ОН–] = h× СМ = 1,67×10-4×0,02 = 3,34×10-6; рОН = –lg 3,34×10-6 = 5,48;
рН = 14 – рОН = 14 – 5,48 = 8,52.
З А Д А Ч И
1. Вычислить константу и степень гидролиза KCN в 0,1 М растворе.
2. Написать уравнение гидролиза в сокращенном ионном виде и указать рН среды для солей: а) NaClO; б) (NH4)2SO4; в) СH3COOK.
3. Указать, какие из приведенных солей будут подвергаться гидролизу: 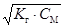 ; [H+] = h × СМ; рН = -lg[H+] = -lg
; [H+] = h × СМ; рН = -lg[H+] = -lg  ,
,  =
=  .
Для этого случая концентрация раствора соли практически не влияет на h:
h =
.
Для этого случая концентрация раствора соли практически не влияет на h:
h = 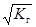 .
Кроме того, [H+] =
.
Кроме того, [H+] =  ; рН = -lg
; рН = -lg  с ионами Н+.
Процесс гидролиза бората натрия можно выразить уравнениями:
I ступень: ВO
с ионами Н+.
Процесс гидролиза бората натрия можно выразить уравнениями:
I ступень: ВO  + OH– ;
II ступень: НВO
+ OH– ;
II ступень: НВO  + OH– ;
III ступень: H2ВO
+ OH– ;
III ступень: H2ВO 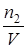 R T = С R T или росм = СМ R T ,
где С – концентрация, моль/м3; СМ– концентрация, моль/дм3; R – универсальная газовая постоянная, Дж/(моль×К); T – абсолютная температура, К.
Уравнение позволяет вычислить для разбавленных растворов неэлектролитов:
1) молекулярную массу растворенного вещества;
2) концентрацию раствора;
3) осмотическое давление раствора.
R T = С R T или росм = СМ R T ,
где С – концентрация, моль/м3; СМ– концентрация, моль/дм3; R – универсальная газовая постоянная, Дж/(моль×К); T – абсолютная температура, К.
Уравнение позволяет вычислить для разбавленных растворов неэлектролитов:
1) молекулярную массу растворенного вещества;
2) концентрацию раствора;
3) осмотическое давление раствора.
 R T . Тогда формула для расчета молярной массы растворенного вещества имеет вид
М2 =
R T . Тогда формула для расчета молярной массы растворенного вещества имеет вид
М2 = 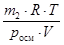 =
= 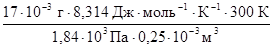 = 92 г/моль.
Пример 2.Вычислить осмотическое давление раствора при 22 °С, в 1,2 дм3 которого содержится 0,021 г сахара С12Н22О11.
Р е ш е н и е
1. Молярная концентрация раствора составит
СМ =
= 92 г/моль.
Пример 2.Вычислить осмотическое давление раствора при 22 °С, в 1,2 дм3 которого содержится 0,021 г сахара С12Н22О11.
Р е ш е н и е
1. Молярная концентрация раствора составит
СМ =  = 5×10-5 моль/дм3.
2. росм = СМ R T = 5×10-5 моль/дм3 × 8,314 Дж / (моль × К) × 295 К = 0,13 кПа.
Пример 3.Определить массу глюкозы С6Н12О6 , которую должен содержать 1 дм3 раствора, чтобы быть изотоничным раствору, содержащему в 1 дм3 9,2 г глицерина С3Н8О3.
Р е ш е н и е
1. Определим молярную концентрацию глицерина
СМ(С3Н8О3) =
= 5×10-5 моль/дм3.
2. росм = СМ R T = 5×10-5 моль/дм3 × 8,314 Дж / (моль × К) × 295 К = 0,13 кПа.
Пример 3.Определить массу глюкозы С6Н12О6 , которую должен содержать 1 дм3 раствора, чтобы быть изотоничным раствору, содержащему в 1 дм3 9,2 г глицерина С3Н8О3.
Р е ш е н и е
1. Определим молярную концентрацию глицерина
СМ(С3Н8О3) = 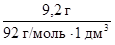 = 0,1 моль/дм3.
2. При одинаковой температуре изотоническими будут растворы с одинаковой молярной концентрацией неэлектролита. Следовательно, масса глюкозы будет равна
= 0,1 моль/дм3.
2. При одинаковой температуре изотоническими будут растворы с одинаковой молярной концентрацией неэлектролита. Следовательно, масса глюкозы будет равна
 ,
где Kк-ты – константа диссоциации слабой кислоты.
Изменение рН раствора соли, происходящее в результате ее гидролиза, может быть вычислено по формуле:
Kг =
,
где Kк-ты – константа диссоциации слабой кислоты.
Изменение рН раствора соли, происходящее в результате ее гидролиза, может быть вычислено по формуле:
Kг =  ; [ОН –] =
; [ОН –] = 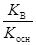 , h =
, h =  =
=  ;
SO
;
SO 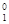 . Связь между р и р
. Связь между р и р  =
= 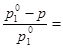 N2 .
N2 .  .
Значения давления насыщенного водяного пара при различных температурах приведены в табл. 1 приложения.
Пример 1.Вычислить давление пара воды над раствором, содержащим 45 г глюкозы С6Н12О6 в 720 г воды при 25 °С.
Р е ш е н и е
Давление пара воды при 25 °С составляет р
.
Значения давления насыщенного водяного пара при различных температурах приведены в табл. 1 приложения.
Пример 1.Вычислить давление пара воды над раствором, содержащим 45 г глюкозы С6Н12О6 в 720 г воды при 25 °С.
Р е ш е н и е
Давление пара воды при 25 °С составляет р  ×
× 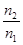 = р
= р  ,
р = 3168 – 3168×
,
р = 3168 – 3168×  = 3148,2 Па .
= 3148,2 Па .
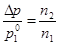 =
=  ,
,  ,
отсюда М2 = 92,04 г/моль.
3. Температура кипения и замерзания. II закон Рауля
Согласно II закону Рауля, повышение температуры кипения DTкип и понижение температуры замерзания DTзам раствора по сравнению с чистым растворителем прямо пропорционально моляльной концентрации растворенного вещества – неэлектролита:
DTкип = Tкип – Т
,
отсюда М2 = 92,04 г/моль.
3. Температура кипения и замерзания. II закон Рауля
Согласно II закону Рауля, повышение температуры кипения DTкип и понижение температуры замерзания DTзам раствора по сравнению с чистым растворителем прямо пропорционально моляльной концентрации растворенного вещества – неэлектролита:
DTкип = Tкип – Т  = E × b;DTзам = Tзам – Т
= E × b;DTзам = Tзам – Т  = K × b,
где Ткип , Т
= K × b,
где Ткип , Т  ; M2 = K ×
; M2 = K ×  .
Пример.Определить температуру кипения и температуру замерзания раствора, содержащего 1 г нитробензола С6Н5NO2 в 10 г бензола. Температура кипения чистого бензола 80,2 °С, температура замерзания чистого бензола 5,4 °С.
Р е ш е н и е
.
Пример.Определить температуру кипения и температуру замерзания раствора, содержащего 1 г нитробензола С6Н5NO2 в 10 г бензола. Температура кипения чистого бензола 80,2 °С, температура замерзания чистого бензола 5,4 °С.
Р е ш е н и е

 =
=  = = 7,4×10-8 .
PbI2осаждается, так как соблюдается условие выпадения осадка:
7,4×10-8 >8,7×10-9.
З А Д А Ч И
1. Растворимость AgI равна 1,2×10-8 моль/дм3. Вычислить ПР(AgI).
2. В 2 дм3 воды при 25 °С растворяется 2,2×10-4 г бромида серебра. Вычислить ПР(AgBr).
3. Произведение растворимости PbCl2 равно 1,7×10-5. Чему равна концентрация ионов свинца в насыщенном растворе PbCl2?
4. Произведение растворимости CaSO4 равно 6×10-5. Выпадает ли осадок CaSO4, если смешать равные объемы 0,2 н. растворов CaCl2 и Na2CO3?
5. ПР (PbI2) = 8,7×10-5. Выпадет ли осадок, если смешать равные объемы растворов, содержащих 3 г/дм3 Pb(NO3)2 и 1 г/дм3 KI?
6. Произведение растворимости AgCl равно 1,6×10-10. Вычислить концентрацию насыщенного раствора AgCl (в моль/дм3 и в г/дм3).
7. Сколько воды потребуется для растворения 1 г СаС2О4 при комнатной температуре, если ПР(СаС2О4) = 2,6×10-9?
8. Сколько граммов СаСО3 может раствориться в 1 дм3 воды при 18 °С, если ПР(СаСО3) = 4,8×10-9 при той же температуре?
9. Вычислить концентрацию ионов Ag+ в насыщенном растворе AgBr, содержащем NaBr концентрации 0,01 моль/дм3.
10. Рассчитать значение ПР, если растворимость вещества Ме2А в воде при некоторой температуре равна 1,2×10-3 моль/дм3.
11. Рассчитать значение ПР гидроксида металла Ме(ОН)2, если рН его насыщенного раствора равен 9,54 при 25 °С.
12. Рассчитать ПР(PbSO4), если массовая доля PbSO4 в насыщенном растворе при некоторой температуре равна 0,057 % (плотность раствора принять равной 1 г/см3).
13. Определить, выпадет ли осадок после сливания равных объемов 0,0023 М растворов AgNO3 и KBr при 25 °С.
14. Определить, выпадет ли осадок после сливания 5 см3 0,004 М раствора CdCl2 и 15 см3 0,003 М раствора NaOH при 25 °С.
= = 7,4×10-8 .
PbI2осаждается, так как соблюдается условие выпадения осадка:
7,4×10-8 >8,7×10-9.
З А Д А Ч И
1. Растворимость AgI равна 1,2×10-8 моль/дм3. Вычислить ПР(AgI).
2. В 2 дм3 воды при 25 °С растворяется 2,2×10-4 г бромида серебра. Вычислить ПР(AgBr).
3. Произведение растворимости PbCl2 равно 1,7×10-5. Чему равна концентрация ионов свинца в насыщенном растворе PbCl2?
4. Произведение растворимости CaSO4 равно 6×10-5. Выпадает ли осадок CaSO4, если смешать равные объемы 0,2 н. растворов CaCl2 и Na2CO3?
5. ПР (PbI2) = 8,7×10-5. Выпадет ли осадок, если смешать равные объемы растворов, содержащих 3 г/дм3 Pb(NO3)2 и 1 г/дм3 KI?
6. Произведение растворимости AgCl равно 1,6×10-10. Вычислить концентрацию насыщенного раствора AgCl (в моль/дм3 и в г/дм3).
7. Сколько воды потребуется для растворения 1 г СаС2О4 при комнатной температуре, если ПР(СаС2О4) = 2,6×10-9?
8. Сколько граммов СаСО3 может раствориться в 1 дм3 воды при 18 °С, если ПР(СаСО3) = 4,8×10-9 при той же температуре?
9. Вычислить концентрацию ионов Ag+ в насыщенном растворе AgBr, содержащем NaBr концентрации 0,01 моль/дм3.
10. Рассчитать значение ПР, если растворимость вещества Ме2А в воде при некоторой температуре равна 1,2×10-3 моль/дм3.
11. Рассчитать значение ПР гидроксида металла Ме(ОН)2, если рН его насыщенного раствора равен 9,54 при 25 °С.
12. Рассчитать ПР(PbSO4), если массовая доля PbSO4 в насыщенном растворе при некоторой температуре равна 0,057 % (плотность раствора принять равной 1 г/см3).
13. Определить, выпадет ли осадок после сливания равных объемов 0,0023 М растворов AgNO3 и KBr при 25 °С.
14. Определить, выпадет ли осадок после сливания 5 см3 0,004 М раствора CdCl2 и 15 см3 0,003 М раствора NaOH при 25 °С.
 = 2,57 кг × К/моль×
= 2,57 кг × К/моль×  2,09 К.
3. Температура кипения раствора равна
Ткип= DTкип+ Т
2,09 К.
3. Температура кипения раствора равна
Ткип= DTкип+ Т  4,14 К .
5. Температура замерзания раствора равна
Тзам= Т
4,14 К .
5. Температура замерзания раствора равна
Тзам= Т  1,3×10-4 моль/дм3.
Пример 3.Определить рН насыщенного раствора гидроксида кальция при 25 °С, если ПР = 6,3×10-6.
Решение
Са(ОН)2(тв)Û Са2+ + 2ОН– ;
рН = [Са2+] × [ОН–]2 = 1/2×[ОН–] × [ОН–]2 = 1/2×[ОН–]3;
рН = 14 – рОН = 14 + lg[ОН–] = 14 + lg
1,3×10-4 моль/дм3.
Пример 3.Определить рН насыщенного раствора гидроксида кальция при 25 °С, если ПР = 6,3×10-6.
Решение
Са(ОН)2(тв)Û Са2+ + 2ОН– ;
рН = [Са2+] × [ОН–]2 = 1/2×[ОН–] × [ОН–]2 = 1/2×[ОН–]3;
рН = 14 – рОН = 14 + lg[ОН–] = 14 + lg  = 14 + lg
= 14 + lg  = 12,4.
Пример 4.Выпадет ли осадок иодида свинца (II) при 25 °С после сливания 100 см3 0,005 М раствора нитрата свинца (II) и 200 см3 0,01 М раствора иодида калия, если ПР (PbI2) = 8,7×10-9?
Решение
Pb(NO3)2 + 2KI = PbI2(тв)+ 2KNO3;
Pb2+ + 2I– = PbI2(тв);
[Pb2+] =
= 12,4.
Пример 4.Выпадет ли осадок иодида свинца (II) при 25 °С после сливания 100 см3 0,005 М раствора нитрата свинца (II) и 200 см3 0,01 М раствора иодида калия, если ПР (PbI2) = 8,7×10-9?
Решение
Pb(NO3)2 + 2KI = PbI2(тв)+ 2KNO3;
Pb2+ + 2I– = PbI2(тв);
[Pb2+] =  ,
где с1и с2 – концентрации ионов в растворах до смешивания; V1и V2 – объемы
,
где с1и с2 – концентрации ионов в растворах до смешивания; V1и V2 – объемы