Электростатическое поле равномерно заряженной бесконечно длинной нити

(расчет на основе теоремы Гаусса).

Учитывая осевую симметрию поля нити, в качестве гауссовой поверхности выбираем цилиндрическую поверхность, ось которой совпадает с нитью (рис. 14.6). Радиус цилиндра – r. Высота цилиндра – .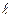

Рис. 14.6. К расчету поля нити

Полный поток вектора , проходящий через цилиндрическую поверхность, можно представить как сумму потоков через основания и через боковую поверхность:

. (14.20)

Поток вектора через основания цилиндра равен

, (14.21)

так как .

Поток вектора , проходящий через боковую поверхность цилиндра, равен

,(14.22)

где E_n = E, поскольку , а при фиксированном r Е = const.

Площадь боковой поверхности цилиндра

. (14.23)

Таким образом

, (14.24)

где

(14.25)

– линейная плотность заряда.

Модуль вектора напряженности электростатического поля нити равен

.(14.26)

Результаты расчетов по методу суперпозиции (14.19) совпадают с результатами расчетов с использованием теоремы Гаусса (14.26).