Электромагнитные и тепловые реле

Из выражения (23) для определения времени торможения привода следует, что при торможении вхолостую время снижения скорости определяется величиной запасенной кинетической энергии, пропорциональной моменту инерции j, и механическими потерями в приводе, т.е.

(27)

Зная величину небольшого снижения скорости за краткий отрезок времени, когда переходный процесс w = f(t) можно считать линейным, на основании выражения (27)

. (28)

Пример 6. Определить момент инерции двигателя, если его скорость за 4 с после отключения от сети снижается на 300 об/мин. При работе двигателя вхолостую со скоростью 1400 об/мин он потребляет из сети мощность 3,6 кВт, половина которой по опытным данным расходуется на преодоление механических потерь.

Решение. Величина момента механических потерь

Момент инерции двигателя при указанном темпе снижения скорости на основании выражения (28):

Более точно величину момента инерции двигателя или электропривода вместе с ИМ можно определить по экспериментальным данным, полученным при опыте выбега (самоторможения) и при изменении потерь холостого хода.

Пример 7. По опытным данным, приведенным в таблице 6.1 и 6.2, определить момент инерции электропривода в различных системах единиц и пересчитать его на маховой момент во внесистемных единицах.

Таблица 6.1

Опыт самоторможения (выбега)

Время от начала выбега, с

Скорость двигателя, об/мин

Таблица 6.2

Опыт холостого хода

Скорость двигателя, об/мин		1 242
Мощность механических потерь, Вт

Решение. На основании опытных данных строятся кривая выбега ω = f(t) и характеристика механических потерь Р = f(ω). по которым строится расчетная кривая P = f(t), показанная на рисунке 6.

Рис. 6. Расчетная кривая выбега

Так как в процессе выбега накопленная кинетическая энергия расходуется на механические потери (трение о воздух и в подшипниках привода), то она может быть определена по площади S расчетной кривой P = f(t), построение которой показано на рисунке 6.

То есть S = , откуда определяется искомый момент инерции привода. Площадь S на кривой Р = f(t) определяется как сумма площадей трапеций при изменении скорости в пределах от ω₁ = 170 с^-1 (t = 0, начало расчета по кривой выбега) до ω₂ = 25с^-1 (t = 52). Ведя расчет таким образом, находим

S = = = J ^.14137,5 Дж∙c².

Подставляем в полученное выражение значение S = 4657,5 м²:

4657,5 = J ^.14137,5.

Отсюда получаем значение J:

J = 0,329 Дж ^. с² (Н ^.м ^.с²).

Маховой момент привода GD² = 4J = 4^.0,329 = 1,316 кг^.м².

В технической системе единиц

кгс^.м^. c².

В ряде случаев, например для подъемных установок, момент инерции электропривода с ИМ можно определить экспериментально, используя так называемый метод падающего груза. Он дает хорошие результаты, если механические потери при вращении невелики (например, при использовании шарикоподшипников). На поверхность шкива (Рис.7) наматывают несколько витков шнура и подвешивают груз с известной массой т. Затем измеряется время t падения груза с высоты h. Так как падение груза происходит с ускорением, уравнение движения вала шкива

, (29)

где ускорение поступательного равноускоренного движения груза определяется по параметрам h и t из опыта:

. (30)

Момент сопротивления движению, создаваемый трением в подшипниках, определяется по минимальной массе т_о, при которой начинается движение шкива на опыте:

. (31)

Вращающий момент М, обеспечивающий ускоренное движение шкива и груза:

. (32)

Преобразуя уравнение (29) с помощью уравнений (30)…(32), получим следующее выражение для определения момента инерции, кг ^.м²:

. (33)

Пример 8. Определить момент инерции двигателя, который при поднятых щетках раскручивается грузом массой т = 1,2 кг, подвешенным на шкиве радиусом R = 0,08 м. За 4 с груз успевает опуститься на высоту h = 7,2 м. Масса груза, при которой преодолевается момент сопротивления в подшипниках, т_о = 0,1 кг.

Решение. Линейное ускорение при падении груза

м/с².

Момент инерции двигателя со шкивом в соответствии с уравнением (33)

кг^.м².

Если определять момент инерции приближенно, без учета потерь в подшипниках, то есть, принимая т_о= 0, получим:

кг^.м².

Для простых геометрических тел вращения, состоящих из однородных материалов, для определения момента инерции (J = mp², где p - радиус инерции) можно пользоваться формулами, приведенными в таблице 6.3.

Таблица 6.3

Формулы для расчета момента инерции тел вращения

Сплошной цилиндр
Полый цилиндр
Сплошной конус

Пример 9. Определить, во сколько раз изменится момент инерции якоря двигателя при увеличении его диаметра в 1,5 раза при неизменной длине, а также при таком же увеличении длины якоря и неизменном диаметре его. Якорь двигателя принять за сплошное однородное тело.

Решение. В соответствии с формулами таблице 3,

Таким образом, при заданных условиях увеличение радиуса якоря в 1,5 раза ведет к увеличению его момента инерции примерно в 5 раз. Аналогичные расчеты показывают, что увеличение длины якоря в 1,5 раза при неизменном диаметре во столько же увеличивается и его момент инерции.

Варианты индивидуального задания

Задание на самостоятельную работу студента состоит из трех задач. Номера задач, входящих в задание, определяются в соответствии с таблицей 7.1.

Таблица 7.1

Варианты заданий

Номер варианта

Номера задач

Продолжение таблицы 7.1

Номер варианта

Номера задач

Задача 1. Кривая самоторможения (выбега) привода, снятая экспериментально, представлена в таблице 7.2, а данные опыта холостого хода – в таблице 7.3. Определить по этим данным момент инерции привода и ИМ.

Таблица 7.2

Кривая самоторможения

Время, с		0,5
Скорость двигателя, об/мин

Таблица 7.3

Механические потери при холостом ходе

Скорость двигателя, об/мин
Механические потери, кВт	1,0	2,5		6,7	9,0

Задача 2. Определить момент и радиус инерции барабана, показанного на рисунке 8. Материал барабана – сталь плотностью 7,8 г/см³ .

Рис. 8. Барабан

Задача 3. Определить пусковой момент, постоянно действующий на систему подъема, изображенную на рисунке 9, необходимый для того, чтобы разогнать ее до скорости = 1,4 м/с при следующих исходных данных: время разгона должно быть равно 2,5 с; поднимаемый груз имеет массу 1т; маховый момент приводного двигателя мощностью 4,9 кВт ( = 900 об/мин) = 1,73 кгc∙м∙c²; маховый момент барабана = 450 кгc∙м∙c², его диаметр = 700 мм; коэффициент трения груза о поверхность = 0,15; КПД передачи между валом барабана и электродвигателем = 0,7; угол подъема наклонной плоскости = 5 .

Рис. 9. Подъемное устройство

Задача 4. Определить вращающий момент на валу двигателя лебедки с противовесом на барабане при разгоне груза массой = 1 т с ускорением =1 м/ (рис.6.3). Масса противовеса = 0,6 т, диаметры барабанов = 0,8 м, = 0,6 м. Коэффициент трения груза о плоскость = 0,2. Угол наклона плоскости = 60.

КПД барабана = 0,95. КПД редуктора между барабаном и двигателем = 0,9. Передаточное число редуктора = 27 (на Рис.10 не показан).

Рис. 10. Лебедка

Задача 5. Определить момент, который должен развивать двигатель лебедки (Рис. 11) при подъеме груза с ускорением = 1 м/с². Статический момент сопротивления, приведенный к валу двигателя, 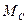= 191,3 Н·м. Момент инерции лебедки с грузом, приведенный к валу двигателя =0,0773 кгc·м∙с², момент инерции двигателя =1,962 кгc·м∙с², диаметр барабана = 0,4м, передаточное число редуктора = 2,57.

Рис. 11. Редуктор

Задача 6. Определить момент вращения, необходимый для разгона в течение 5 с мостового крана массой = 26 т, с полезным грузом массой = 2 т, двигателем мощностью Рн = 13,2 кВт, n_дн= 725 об/мин. Номинальная скорость передвижения крана 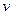= 75 м/мин. Статический момент при пуске равен номинальному моменту. Схема передачи и размеры ее элементов показаны на рисунке 12. Коэффициент трения качения колеса крана о рельсы = 0,05 см. Коэффициент трения скольжения в цапфах колес = 0,08. Коэффициент, учитывающий трение в ребордах колес, = 1,3. Диаметр колеса = 65 см, диаметр цапфы оси колеса = 7,5 см. КПД каждой ступени передачи = 0,95. Маховый момент ротора двигателя = 12 кг·м², момент инерции тормозного диска = 0,08 кгc·м∙с², маховый момент первого зубчатого колеса Z₁ – = 0,9 кг·м², второго = 6,8 кг·м². Маховыми моментами остальных вращающихся масс пренебречь.

Задача 7. Определить величину момента на валу между двигателем и маховиком, а также на валу между маховиком и первой шестерней механизма прокатного стана (рис.12) при пуске двигателя вхолостую и под нагрузкой, пренебрегая потерями в двигателе и маховике. Момент, развиваемый двигателем при пуске, = 5493,6 Дж. Статический момент, приведенный к валу двигателя при пуске под нагрузкой, = 312,2 H∙м. Момент инерции маховика, приведенный к валу двигателя, = 78,9 кгc·м∙с², остальной части механизма = 0,5 кгc·м∙с². Момент инерции ротора двигателя = 100 Дж∙с² .

Рис.12 Механизм прокатного стана

Задача 8. Определить мощность, развиваемую электродвигателем лебедки (Рис.13) при подъеме и спуске груза с постоянной скоростью 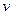= 0,9 м/с, и момент, который должен развивать двигатель при пусках на подъем и спуск с ускорением 0,5 м/с². Статический момент, приведенный к валу двигателя при подъёме, = 42 H·м. А при спуске он является активным и равен 34 H·м. Приведенный к валу двигателя момент инерции механизма = 0,0815 кгc·м∙с². Момент инерции ротора двигателя = 3,294 Н·м∙с². Скорость двигателя =1430 об/мин.

Рис. 13. Подъемный механизм

Задача 9. Определить мощность, развиваемую двигателем шахтного подъёмника с уравновешенным канатом (Рис.14) при подъёме скипа с установившейся скоростью 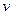= 6 м/с, и момент, который должен развивать двигатель при пуске на подъём, чтобы обеспечить ускорение скипа в 1,2 м/с. Статический момент, приведенный к валу двигателя, =1013 H·м. Скорость двигателя = 485 об/мин. Момент инерции двигателя =30 кгc·м·с². Диаметр барабана = 4 м. Передаточное число редуктора от барабана к двигателю =16,9.

Рис. 14. Шахтный подъемник

Задача 10. Двигатель постоянного тока ( = 6 кВт, = 1430 об/мин, = 220 В, = 0,4 кг·м²) приводит в движение тележку и разгоняется с постоянным динамическим моментом 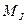= 7 H · м до своей номинальной скорости. При этом скорость тележки достигает 1,5 м/с. Статический момент при разгоне = 4 H·м. Маховый момент механизма, приведенный к валу двигателя, = 3,1 кг·м². Определить путь, пройденный тележкой за период разгона.

Задача 11. Имеется подъёмник (Рис. 15), в котором груз массой полностью уравновешивается грузом массой . Оба груза висят на тросе, перекинутом через блок А. Масса каждого груза 1,5 т. Ось блока приводится в движение двигателем через редуктор (на рис. не показаны) с КПД = 0,9.

Рис. 15. Подъемник

Определить: какую силу надо приложить к грузам, чтобы началось их движение с ускорением = 1 м/с; какова должна быть мощность двигателя для перемещения грузов с установившейся скоростью 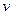= 0,2 м/с? Сопротивление трения, а также масса блока А и каната не учитываются.

Задача 12. Определить необходимый динамический момент, который должен быть приложен к валу электродвигателя, соединенному с зубчатым колесом 1 строгального станка (кинематика показана на рисунке 16), для того, чтобы разогнать его до номинальной скорости 420 об/мин в течение 1,2 с.

Рис. 16. Кинематическая схема

Маховый момент якоря электродвигателя =11,5 кг·м², КПД одной пары зубчатых колес 0,96. Масса стола станка с грузом = 3 030 кг. Шаг зацепления колеса 8 - = 25,13 мм. Числа зубцов шестерен передачи и маховые моменты шестерен следующие (табл. 7.4):

Таблица 7.4

Параметры шестерен

Z1 = 20	= 0,42 кг·м²	Z5 = 30	= 1,9 кг·м²
Z2 = 55	= 2,05 кг·м²	Z6 = 78	= 4,2 кг·м²
Z3 = 30	= 1,0 кг·м²	Z7 = 30	= 2,5 кг·м²
Z4 = 64	= 2,9 кг·м²	Z8 = 60	= 6,5 кг·м²

Задача 13. Определить время торможения привода лебедки при силовом спуске груза, если момент инерции двигателя равен 0,105 кг·м·с², а тормозной момент, развиваемый двигателем, составляет 500 Дж. Начальная скорость двигателя 970 об/мин, М_н = 200 H·м.

Задача 14. Определить время торможения до остановки электропривода, если средний тормозной момент двигателя = 882,9 Дж, приведенный к валу двигателя момент статического сопротивления 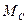= 294,3 Н·м, маховый момент на валу двигателя = 50 кг· . Начальная скорость двигателя = 582 об/мин.

Задача 15. Определить время разгона электропривода до скорости =720 об/мин, если среднее значение момента, развиваемого двигателем при спуске, M = 44 кг·м, а маховый момент привода, приведенный к валу двигателя, = 35 кг·м². Статический момент на валу двигателя = 8 H·м.

Задача 16. Определить путь двигателя в оборотах за время разбега вхолостую из неподвижного состояния до скорости = 975 об/мин. Среднее значение момента, развиваемого двигателем при пуске, = 25 H·м, момент инерции, приведенный к валу двигателя, = 1,147 кгc·м·с².

Задача 17. Установившаяся скорость кабины лифта составляет 3,5 м/с, а ускорение при пуске = 2,5 м/с. Определить время и путь кабины и ротора двигателя, а также силу инерции пассажира массой 75кг при пуске кабины на подъём. Привод лифта безредукторный. Вал барабана лебедки соединен с валом двигателя муфтой, диаметр барабана 0,8 м.

Задача 18. Асинхронный двигатель (Рн2 = 16,5 кВт, n_н = 955 об/мин) с маховым моментом =1,54 кг∙м² связан с производственным механизмом через трехступенчатую зубчатую передачу с передаточным числом = 90. КПД каждой зубчатой пары = 0,95. Маховый момент механизма =90 900 кг∙м². Статический момент, действующий на валу производственного механизма перед началом торможения, = 700 H·м. Определить величину постоянно действующего момента на валу двигателя, необходимого для остановки электропривода в течение двух секунд.

Задача 19. Определить время разгона привода подъёмника при спуске кабины для двух случаев:

а) двигатель развивает тормозной момент =10 H·м;

б) двигатель развивает движущий момент =10 H·м.

Статический момент на валу двигателя активный 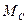= 196,2 Дж. Момент инерции, приведенный к валу двигателя, = 0,51 кгc·м·с². Установившаяся скорость движения = 780 об/мин.

Задача 20. Двигатель работает с моментом сопротивления на валу 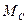= 17 H·м. Определить, какой тормозной момент должен быть постоянно приложен к валу двигателя для того, чтобы, отключив двигатель при скорости = 900 об/мин, остановить его в течение 1с. Суммарный момент инерции, приведенный к валу двигателя, равен 0,32 кгc·м·с².

Задача 21. Определить ускорение и путь, пройденный столом строгального станка. Электромагнитный момент, развиваемый двигателем при пуске, =18 H·м. Статический момент, приведенный к валу двигателя, 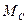=8,4 кгH·м. Передаточное число передачи = 87,5. Диаметр последней шестерни Z₈D₈= 500 мм. Приведенный к валу двигателя маховый момент всего механизма и обрабатываемой детали = 0,73 кг·м². Маховой момент ротора двигателя =6 кг·м². Скорость двигателя = 557 об/мин. Потерями в передачах пренебречь.

Задача 22. Определить ускорение тележки при разгоне, если момент, развиваемый двигателем, =2,5 H·м. Статический момент, приведенный к валу двигателя, 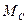= 0,95 кг·м, момент инерции = 0,528 Дж∙с². Момент инерции двигателя = 0,12 кгc·м∙с². Скорость перемещения тележки 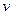= 80 м/мин, скорость двигателя = 960 об/мин. Допустить, что при разгоне проскальзывание между колесами тележки и рельсами отсутствует.

Задача 23. Определить время разгона двигателя лебёдки, момент сопротивления которого на валу 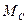=282 Дж. Пусковой момент двигателя равен М_п = 2 М_н. Лебедка приводится в движение асинхронной машиной мощностью = 22 кВт, = 715 об/мин, = 6,0 кг·м². Момент инерции механизма, приведенный к валу двигателя, составляет 40% от момента инерции двигателя.

Задача 24. На вал двигателя передвижения мостового крана действует момент статического сопротивления 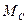= 13,3 H·м. Определить, можно ли разогнать кран за 3 с до установившейся скорости двигателя =740 об/миn при его мощности = 8,5 кВт и маховом моменте ротора =3,1 кг·м², если максимальный момент, который может развивать двигатель, = 3 М_н. Установившаяся скорость крана 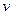= 1,3 м/с, масса моста с грузом = 28 т. Момент инерции соединенных муфт и зубчатых передач составляет 20% от момента инерции двигателя.

Задача 25. Момент сопротивления на валу двигателя передвижения портального крана 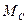= 6 H·м. Определить время разгона до установившейся скорости =1 м/с, соответствующей номинальной скорости двигателя = 730 об/мин, а также путь крана за период разгона. Масса крана с грузом = 24,3 т. Мощность двигателя = 4 кВт, пусковой момент принять равным М_п = 2 М_н; = 0,115 кг∙м², = 0,2 .

Задача 26. Портальный кран с грузом, данные которого указаны в задаче 25, замедляется путем свободного выбега при отключении двигателя от сети. Определить время замедления и путь, проходимый при этом краном.

Задача 27. Поворотный кран приводится в действие двигателем, имеющим Р_н = 4 кВт, n_н = 920 об/мин, = 0,46 кг·м². При вращении с установившейся скоростью двигатель развивает на валу мощность в 2,8 кВт. Передаточное число от вала двигателя до оси вращения крана =1000. Момент инерции поворотной части крана =73575 Дж·с², вылет стрелы =12 м. Определить, необходимо ли искусственное торможение электропривода поворота, чтобы остановить кран на пути 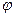< 8 . Перемещение стрелы при малых углах принять идущим по прямой линии.

Задача 28. Двигатель ( =11 кВт, =1440 об/мин) через редуктор с передаточным числом =16 приводит в движение ходовые колеса тележки мостового крана, которая вместе с установленным на ней оборудованием и перемещаемым грузом имеет массу 20 т (масса груза составляет 6 т). Диаметр ходовых колес = 0,35 м. При перемещении тележки с грузом статический момент на валу двигателя = 4,4H·м, а без груза = 3,2 H·м. Приведенный к валу двигателя момент инерции вращающихся частей (включая и ротор двигателя) равен 2 Дж^.с². Средний пусковой момент двигателя = 1,6 М_н, а тормозной = М_н.

Определить продолжительность пуска и торможения тележки с грузом и без него, а также путь, проходимый тележкой в этих случаях.

Задача 29. Определить кинетическую энергию мостового крана массой = 30 т с грузом = 30 т, движущегося со скоростью 1,5 м/с. Определить кинетическую энергию ротора электродвигателя этого крана, если скорость вращения равна 700 об/мин, а маховой момент = 12,25 кг·м².

Задача 30. Определить, какая мощность потребуется для подъема лифта с грузом массой m_r = 2 т со скоростью v = 0,3 м/с при собственной массе кабины m_к= 1,9 т при системе привода без противовеса. КПД подъемного механизма η = 0,45.

Задача 31. Определить, во сколько раз изменится момент инерции якоря двигателя при увеличении длины якоря в 2 раза и неизменном его диаметре. Якорь двигателя принять за сплошное однородное тело.

Задача 32. Определить, во сколько раз изменится момент инерции якоря двигателя при увеличении диаметра якоря в 1,5 раза и неизменной его длине. Якорь двигателя принять за сплошное однородное тело.

Список рекомендуемой литературы:

Основная:

1. Чунихин А.А. Электрические аппараты. Общий курс [Текст] : учебник для студентов электротехнических и электроэнергетических специальностей вузов / А. А. Чунихин. - 4-е изд., стер., перепеч. с третьего изд. 1988 г. - М. : Альянс, 2008. - 719 с.

2. Казаков А.А. Электрические аппараты [Текст] : учебное пособие для студентов вузов, обучающихся по направлению подготовки 140600 "Электротехника, электромеханика и электротехнологии" / В. А. Казаков. - М. : РадиоСофт, 2009. - 372 с.

3. Епифанов А.П. Основы электропривода [Текст] : учебное пособие для студентов вузов, обучающихся по специальности 110302 - "Электрификация и автоматизация сельского хозяйства" / А. П. Епифанов. - 2-е изд., стер. - СПб. [и др.] : Лань, 2009. - 192 с.

4. Кацман М.М. Электрический привод [Текст] : учебник для студентов образовательных учреждений СПО / М. М. Кацман. - 3-е изд., стер. - М. : Академия, 2010. - 384 с.