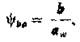ОБЩИЕ СВЕДЕНИЯ

 

Различают два вида зубчатых передач - закрытые и откры­тые. Эти передачи обычно разрабатывают в курсовых проектах учащиеся техникумов.

Закрытые, заключенные в отдельный корпус (например, редукторного типа) или встроенные в машину. Проектировочный расчет их выполняют на выносливость по контактным напря­жениям во избежание усталостного выкрашивания рабочих поверхностей зубьев. Определив на основе этого расчета размеры колес и параметры зацепления, выполняют затем про­верочный расчет на выносливость зубьев по напряжениям изгиба для предотвращения усталостного разрушения зубьев; обычно напряжения изгиба в зубьях, рассчитанных на контакт­ную прочность, оказываются ниже допускаемых. Однако при выборе слишком большого суммарного числа зубьев колес (более 200) или применении термохимической обработки поверх­ностей зубьев до высокой твердости (HRC>45) может возник­нуть опасность излома зубьев. Для предотвращения этого раз­меры зубьев следует определять из расчета их на выносливость по напряжениям изгиба.

Открытые зубчатые передачи рассчитывают на выносливость по напряжениям изгиба с учетом износа зубьев в процессе эксплуатации. В этом случае нет необходимости проверять выносливость поверхностей зубьев по контактным напряжениям, так как абразивный износ поверхностей зубьев предотвращает выкрашивание их от переменных контакт­ных напряжений.

Зубчатые передачи, работающие с большими кратковремен­ными (пиковыми) перегрузками, необходимо проверять на от­сутствие опасности хрупкого разрушения или пластических деформаций рабочих поверхностей зубьев от контактных напряжений, а также на отсутствие хрупкого излома или пласти­ческих деформаций при изгибе. Это относится равно как к закры­тым, так и открытым передачам.

 

 

Рис. 3.1. Контактные напряжения в зоне соприкосновения цилиндров вдоль образующей

Кратковременное действие пиковых нагрузок не оказывает влияния на поверхностную и общую усталостную прочность зубьев. Поэтому определение напряжений, вызываемых такими нагрузками, следует рассматривать как проверку зубьев на по­верхностную и общую статическую прочность. Расчетные формулы имеют тот же вид, что и формулы для расчетов на усталостную прочность, но значения допускаемых напряжений, принимаемых в этих расчетах, различны.

Расчет закрытых зубчатых передач на выносливость рабо­чих поверхностей зубьев по контактным напряжениям основан на формуле Герца. Эта формула служит для определения макси­мального нормального напряжения в точках средней линии контактной полоски в зоне соприкосновения двух круговых цилиндров с параллельными образующими (рис. 3.1). При выводе формулы были приняты допущения: материал цилиндров идеально упругий, в точках контакта он находится в условиях объемного напряженного состояния — трехосного сжатия; наибольшее (по модулю) напряжение сжатия — главное напря­жение s₃ — принято обозначать s_mах; при эллиптическом за­коне распределения давления по ширине площадки контакта

 

(3.1)

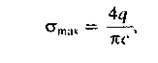
где q – нагрузка на едницу длины контактной линии; с – ширина контактной площадки, определяемая из выражения

 

 

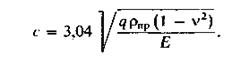
Подставив это значение в формулу (3.1.), получим

 

(3.2)

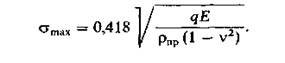
1 1 1 1

Здесь ^______ - приведенная кривизна цилиндров, ^______ = ^______ + ^______, где r₁ и

r_пр r_пр r₁ r₂

r₁ r₂

r₂ – радисы цилиндров; отсюда - r_пр = ^_________ ; v – коэффициент Пуассона, при-

r₁ + r₂

нятый равным 0,3; Е – модуль упругости материала цилиндров; если цилиндры изготовлены из разных материалов, то определяют приведенный модуль упругости

 

§ 3.2. РАСЧЕТ ЦИЛИНДРИЧЕСКИХ ЗУБЧАТЫХ КОЛЕС НА КОНТАКТНУЮ ВЫНОСЛИВОСТЬ

 

Для расчета передач с цилиндрическими зубчатыми коле­сами (рис. 3.2) на выносливость рабочих поверхностей зубьев по контактным напряжениям пользу­ются формулой (3.2); максималь­ное нормальное напряжение s_тax принято обозначать s_н; индекс H (лат.) соответствует первой букве фамилии знаменитого физика Hertz'a; нагрузка на единицу дли­ны контактной линии зубьев

 

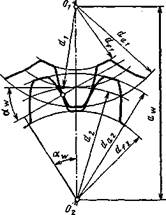
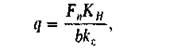
где 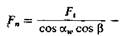нормальная сила в зацеплении;

Рис. 3.2. Геометрия зубчатого эвольвентного зацепления

Ft

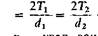- окружная сила; a_w – угол зацепления; по ГОСТ 13755-81 он принят равным 20^о*; b - угол наклона зуба по отношению к образующей делитель-ного цилиндра; К_н — коэффициент, учитывающий ди-

намиче­скую нагрузку и неравномерность распределения

нагрузки между зубьями и по ширине венца; b — шири-

на венца; k_e - коэф­фициент степени перекрытия.

Приведенный радиус цилиндров r_пр следует заменить величи­ной приведенного радиуса эвольвентных профилей зубьев в полюсе зацепления; так как

 

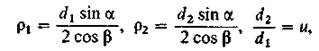
то

 

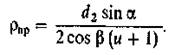
Подстановка приведенных значений величин в формулу (3.2) дает возможность выразить зависимость s_н от параметров зубчатой передачи в виде

 

(3.3)

 

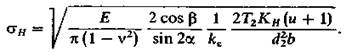
Дальнейшие расчеты даны в соответствии с рекоменда­циями ГОСТ 21354-75. Допущенные в отдельных случаях незначительные отступления, практически не влияющие на величину конечного результата, имеют целью некоторое упро­щение расчета.

* В дальнейшем будем считать a_w » a, где a - делительный угол профиля или угол профиля исходного контура

 

Для практических расчетов по ГОСТ 21354-75 введены сле­дующие условные обозначения:

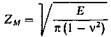— коэффициент, учитывающий механиче­ские свойства материала сопряженных зубчатых колес; его раз­мерность соответствует размерности Ö E;

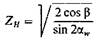– безразмерный коэффициент, учитывающий форму сопряженных поверхностей зубьев в полюсе зацепления;

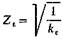— безразмерный коэффициент, учитывающий сум­марную длину

контактных линий; для прямозубых колес k_e = ^__________; для косозубых и шев-

4 - e_a

ронных k_e = e_a, где e_a - степень перекрытия.

С этими обозначениями формула (3.3) примет вид

 

(3.4)

 

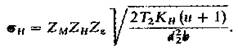
Все величины, входящие в эту формулу, должны быть выра­жены в соответствующих единицах. В ГОСТ 21354-75 допу­щено отклонение от этого правила: момент выражен в Н × м, a d и b в мм, напряжение и модуль упругости в МПа (числен­но соответствует МН/м²).

В дальнейшем, следуя правилу теории размерностей, будем выражать момент в Н × мм, d и b в мм, s_н и Е в МПа (что численно соответствует Н/мм²).

Для стали принимают: Е = 2,15 × 10⁵ МПа; коэффициент Пуассона v = 0,3. При этих значениях коэффициент

 

 

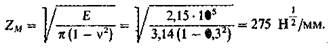
Численные значения коэффициента Z_H:

для прямозубых колес при a = 20°, b = 0 Z_H = 1,76;

для косозубых колес при a = 20°, b = 8¸15° Z_H = 1,74¸1,71;

для шевронных колес Z_H = 1,57.

Средние значения коэффициента Z_e:

для прямозубых передач при a = 20° Z_e = 0,9 ;

для косозубых передач Z_e = 0,8.

После подстановки указанных значений коэффициентов в формулу (3.4) и замены в ней d₂ через межосевое расстояние a_w

 

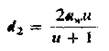
получим формулы для проверочного расчета:

прямозубых передач

(3.5)

 

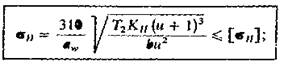
косозубых передач

 

(3.6)

 

Выражая в этих формулах величину b через a_w с помощью коэффициента

 

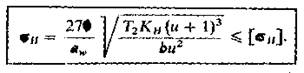
ширины зубчатого венца получим формулу для проектировочного расчета a_w, мм

 

(3.7)

 

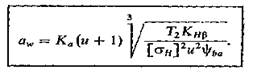
Дляпрямозубых передач К_а = 49,5; для косозубых и шев­ронных передач К_а = 43,0.

Коэффициент К_H = К_Нa,К_НbК_Hv, где К_Ha — коэффициент, учи­тывающий неравномерность распределения нагрузки между зубьями; для прямозубых колес принимают K_Ha = 1,0; для косозубых колес в зависимости от окружной скорости v: при v =10¸20 м/с и 7-й степени точности К_Нa — 1,0¸1,1, при v до 10 м/с и 8-й степени точности K_Ha = 1,05¸1,15; К_Нb — коэф­фициент, учитывающий неравномерность распределения нагруз­ки по ширине венца. При проектировании закрытых зубчатых передач редукторного типа принимают значения K_Hb по табл. 3.1.

3.1. Ориентировочные значения коэффициента K_Hb для зубчатых передач редукторов, работающих при переменной нагрузке

 

Расположение зубчатых колес относительно опор	Твердость НВ поверхностей зубьев
£350	> 350
Симметричное Несимметричное Консольное	1,00-1,15 1,10-1.25 1,20-1,35	1,05-1,25 1,15-1,35 1,25-1,45
Меньшие значения принимают для передач с отношением ybd = b/d1 = 0,4: при увеличении ybd до 0,6 для консольно расположенных колес и ybd до 0,8 при несимметричном расположении их следует прини­мать большие из указанных в таблице значений KHb . При постоянной нагрузке KHb = 1. Определение ybd см. формулу (3.8).

Динамический коэффициент K_Hvопределяют в зависимости от окружной скорости v колес и степени точности их изготов­ления.

Для прямозубых колес при v до 5 м/с следует назначать 8-ю степень точности по ГОСТ 1643-81; при этом K_Hv = 1,05¸1,10.

Для косозубых колес при v до 10 м/с назначают также 8-ю степень точности и принимают K_Hv= 1,0¸1,05. При v свыше 10 до 20 м/с и 7-й степени точности К_Hv. = 1,05¸1,1. Меньшие из указанных значений относятся к колесам с твердостью поверх­ностей зубьев НВ £ 350, большие - при твердости НВ > 350.

Коэффициенты К_Ha и K_Hvмогут быть определены только тогда, когда известны размеры передачи (надо знать скорость v). Поэтому при проектировочных расчетах по формуле (3.7) пред­варительно используют один коэффициент K_Hb, учитывающий неравномерность распределения нагрузки по ширине венца (см. табл. 3.1 ).

При проектировании редукторов обычно задаются величиной y_ba = b / a; для прямозубых передач принимают y_ba = 0,125¸0,25; для косозубых y_ba = 0,25¸0,40; для шевронных y_ba = 0,5¸1,0. Чтобы вычислить y_bd по выбранному

 

значению y_ba следует воспользоваться равенством ; тогда

 

(3.8)

 

Допускаемое контактное напряжение определяют при проек­тировочном расчете по формуле

 

(3.9)

 

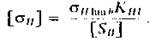
Здесь s_{H lim b}, — предел контактной выносливости при базовом числе циклов (значения s_{H lim b}, указаны в табл. 3.2); К_HL — коэффи­циент долговечности; если число циклов нагружения каждого зуба колеса больше базового, то принимают K_HL = 1. Именно такой случай типичен для курсовых проектов, выполняемых в техникумах.

В других условиях, когда эквивалентное число циклов перемены напряжений N_HE меньше базового N_HO , то

 

 

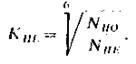
Если при расчете колес из нормализованной или улучшен­ной стали К_HL получается больше 2,6, то принимают К_HL = 2,6; для колес из закаленной стали К_HL £ 1,8; [S_H] - коэффициент безопасности; для колес из нормализованной и улучшенной стали, а также при объемной закалке принимают [S_H] = 1,1¸1,2; при поверхностном упрочнении зубьев [S_H ] = 1,2¸1,3.

Данные для выбора материалов шестерни и колеса приве­дены в табл. 3.3. Рекомендуется назначать для шестерни и колеса сталь одной и той же марки, но обеспечивать соответст­вующей термической обработкой твердость поверхности зубьев шестерни на 20—30 единиц Бринелля выше, чем колеса.