ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ

Из исходного 0,1 М раствора слабого электролита (кислоты или основания) последовательным разбавлением готовят по 100 мл 0,05 М; 0,025 М; 0,0125 М; 0,00625 М; 0,003 М; 0,0015 М растворов.

Все растворы готовят в мерных колбах на 100мл. Для этого рассчитывают объем V₁ исходного раствора кислоты (основания) с молярной концентрацией C₁, необходимый для приготовления объема V₂ раствора заданной концентрации С₂. При расчете исходят из того, что количество кислоты при разбавлении исходного раствора не изменяется:

C₁ ·V₁ = С₂ ·V₂.

V₁ = С₂ ·V₂ / C₁.

Например, для приготовления 100мл 0,05М раствора необходимо взять 50 мл исходного раствора: V₁ = 0,05·100/0,1 = 50 мл.

Для получения более точных результатов концентрации приготовленных растворов устанавливают кислотно-основным титрованием (титруют раствором щелочи или кислоты соответствующей концентрации). Для титрования выбирают раствор щелочи с концентрацией, примерно равной концентрации титруемого раствора.

С_{Н к} = (С_{Н NаОН} V_NаОН)/ V_К ,

где С_{Н NаОН} – эквивалентная (нормальная) концентрация щелочи, моль/л;

С_{Н к}– эквивалентная (нормальная) концентрация кислоты, моль/л;

V_NаОН– средний объем щелочи, пошедший на титрование пробы кислоты, мл;

V_К– объем пробы кислоты, мл.

Для одноосновных кислот (и однокислотных оснований) эквивалентные и молярные концентрации совпадают С_Н = С_М.

Результаты титрования заносят в таблицу 5.

 

Таблица 5 − Результаты титрования

 

№ п/п	Заданная концен-трация раствора, моль/л	Концен- трация щелочи, моль/л	Объем пробы, мл	Объем щелочи, пошедший на титрование	Средний объем щелочи, мл	Точная концен- трация кислоты, моль/л

 

Измеряют электрическую проводимость приготовленных растворов в порядке возрастания концентраций. Перед измерением сосуд и датчик промывают дистиллированной водой и исследуемым раствором. Объем раствора должен быть постоянным, например, 50 мл.

Используя значения удельной электрической проводимости æ_С, рассчитывают молярную электрическую проводимость по формуле:

l_С = æ_с / C_M,

где размерность молярной концентрации [С_M] = кмоль/м³ (1 кмоль/м³ соответствует 1 моль/л).

Вычисляют степень электролитической диссоциации a по формуле:

a = l_С / l₀,

используя экспериментальные значения l_С и справочные значения l₀.

Молярную электропроводность раствора электролита при бесконечном разведении l₀ рассчитывают по закону независимости движения ионов. Молярные электрические проводимости ионов при бесконечном разведении λ₀₊ и λ_0– берут из таблицы Приложения «Молярные электрические проводимости ионов при бесконечном разведении» [2].

Константу диссоциации рассчитывают по закону разведения Оствальда:

К_ДИС = .

Константу диссоциации можно рассчитать по формуле:

К_ДИС = . (*)

Результаты измерений и вычислений оформляют в виде таблицы 6.

 

Таблица 6 – Результаты измерений электропроводности слабого электролита

 

№ п/п	Точная концен-трация раствора, кмоль/м3	Удельная электро-проводность раствора æС, Ом -1 ∙ м -1	Молярная электропровод-ность раствора lС, Ом -1 ∙ м 2∙кмоль-1	Степень диссо- циации aС	КДИС

 

Полученное значение К_ДИС сравнивают со справочным значением из таблицы Приложения «Константы диссоциации слабых кислот и оснований при 25°C» [2], вычисляют абсолютную (∆) и относительную (δ) погрешность определения К_ДИС.

∆ = | К_{ДИС(ТАБЛ)} – К_{ДИС(ЭКСП)} |;

Δ = ·100%.

По результатам измерений и расчетов строят графики (рис. 6) зависимостей l_С = f (С_M), a = (С_M), делают выводы.

 

а) б)

 

Рис.6 – Зависимость молярной электропроводности раствора слабого электролита (а) и степени диссоциации слабого электролита (б) от .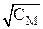

Константу диссоциации слабого электролита К_ДИС и его молярную электропроводность l₀ при бесконечном разведении можно определить графическим методом. Для этого необходимо преобразовать уравнение (*).

К_ДИС ∙l₀∙(l₀ − l_С ) = С_М∙l_С ²;

К_ДИС ∙l₀² − К_ДИС ∙l₀∙l_С = С_М∙l_С ².

Правую и левую части уравнения делят на l_С:

К_ДИС ∙l₀²/l_С − К_ДИС ∙l₀ = С_М∙l_С ;

С_М∙l_С = − К_ДИС ∙l₀ + К_ДИС ∙l₀²/l_С;

Так как С_М∙l_С = æ_с , то æ_с = − К_ДИС ∙l₀ + К_ДИС ∙l₀²/l_С.

По экспериментальным данным строят график зависимости æ_с = f(1/l_С) (рис.7).

Отрезок, отсекаемый на оси ординат, равен −К_ДИС∙l₀, а отрезок, отсекаемый на оси абсцисс, равен 1/l₀. Действительно, если æ_с = 0, то − К_ДИС ∙l₀ + К_ДИС ∙l₀²/l_С = 0 и l₀ = l_С (1/l₀ = 1/l_С).

 

Рис.7 – График зависимости æ_с = f(1/l_С).