Закон Ома для однородного участка цепи в интегральной и дифференциальной форме. Сопротивление проводников

 

Ом экспериментально установил закон, согласно которому сила тока, текущего по однородному металлическому проводнику, пропорциональна падению напряжения U на проводнике:

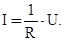(Интегральная форма закона) (20.10)

Однородным называется проводник, в котором не действуют сторонние силы, т.е. отсутствуют источники ЭДС. В этом случае, как мы видели, напряжение U совпадает с разностью потенциалов j₁ - j₂, поддерживаемой на концах проводника. Величина Rназывается электрическим сопротивлением проводника. Единицей сопротивления служит Oм, равный сопротивлению такого проводника, в котором при напряжении в 1 В течет ток силой в 1 А.

Величина сопротивления зависит от формы и размеров проводника, а также от свойств материала, из которого он сделан. Для однородного цилиндрического проводника

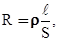(20.11)

где l - длина проводника, S - площадь его поперечного сечения, r - зависящий от свойств материала коэффициент, называемый удельным электрическим сопротивлением вещества. В СИ r измеряется в омо-метрах (Ом×м). На практике часто характеризуют материал сопротивлением при l = 1 м и S == 1 мм², т. е. выражают r в

Закон Ома можно записать в дифференциальной форме.

Это уравнение устанавливает связь между дифференциальными характеристиками поля и тока, т.е. между j и Ев одной и той же точке проводника.

Преобразуем выражение (20.10) применительно к цилиндрическому проводнику, являющемуся однородным участком электрической цепи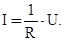

Если поле однородно, то U = E×l, 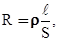и тогда

Обозначим 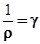и назовем удельной проводимостью, а 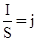- плотность тока.

В результате получаем j = g×E . Вполне справедлива и векторная форма записи

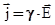(20.12)

В анизотропных телах направления векторов j и Е могут не совпадать.