Аналитическая геометрия на плоскости

Раздел 1. Аналитическая геометрия

 

 

1.1. Построить треугольник с вершинами A(-2;4); B(2;1) и C(5;5) и определить его периметр и углы.

1.2. Найти координаты точки, симметричной точке (-3;5) относительно биссектрисы третьего координатного угла.

1.3. На оси Ох найти точку, одинаково удаленную от начала координат и от точки М(8;4).

1.4. Дан квадрат, сторона которого равна единицам. Чему будут равняться координаты его вершин, если оси координат направить по диагоналям этого квадрата?

1.5. Определить середины сторон треугольника с вершинами А(-1;2), B(5;6) и С(3;0).

1.6. Отрезок прямой с концами в точках А(4;2) и В(13; 8), разделен на три равные части. Определить координаты точек деления.

1.7. Найти координаты точки С, делящей отрезок АВ, А(-2;3), B(5;-4), в отношении λ = -3.

1.8. Даны вершины треугольника: А(6;4), B(3;0), С(2;5). Определить длины медиан и вычислить координаты точки их пересечения.

1.9. Даны вершины треугольника: А(3;3), B(6;-1), С(-5;-3). Найти точку пересечения биссектрисы угла А со стороной ВС и её длину AD.

1.10. Составить уравнение геометрического места точек, одинаково удаленных от оси Ох и от точки F(0;2).

1.11. Написать уравнение линии, по которой движется точка М(х;у), равноудаленная от точек А(0;2) и B(-4;-2).

1.12. Найти уравнение геометрического места точек, расстояние которых от оси Оу в три раза больше, чем от оси Ох.

1.13. Найти, уравнения биссектрис координатных углов.

1.14. Найти уравнение геометрического места точек, для каждой из которых расстояние от точки A(-4;0) вдвое больше, чем от точки В(-1;0).

1.15. Найти уравнение прямой, образующее с осью Ох угол 135° и пересекающей ось Оу в точке (0;4).

1.16. Найти уравнение прямой, проходящей через точки А(-2,-1) и В(1;8).

1.17. Написать уравнение прямой, отсекающей на осях координат отрезки, величины которых соответственно равны 5 и 6.

1.18. Определить параметры k и b прямой, проходящей через точку М(2;1) и составляющей с Ох угол 45°. Написать уравнение этой прямой.

1.19. Дан треугольник с вершинами А(-5;0), В(2; 1), С(-2;3). Написать уравнения сторон треугольника.

1.20. Равнобедренная трапеция с основаниями 8 и 2 имеет острый угол 45°. Написать уравнения сторон трапеции, приняв за ось Ох большее основание и за ось Оу – ось симметрии.

1.21. Написать уравнения сторон ромба с диагоналями 10 и 6, приняв меньшую диагональ за ось Ох и большую за ось Оу.

1.22. Написать уравнение прямой, проходящей через точку М(4;3) и отсекающей от координатного угла треугольник площадью, равной 3 кв. единицам.

1.23. Прямая пересекает ось Оу в некоторой точке С и проходит через точки А(2; 5) и В(-7;-3). Найти координаты точки С.

1.24. Найти угол между двумя прямыми:

а) у =1 5 - 2х и у = 3х + 10,

б) 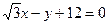и .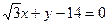

1.25. В точках пересечения прямой 2х + 5у – 10 = 0 с осями Ох и Оу восстановлены перпендикуляры к этой прямой. Найти их уравнения.

1.26. В треугольнике с вершинами A(2;0), В(-2;6) и С(-4;2) проведены высота BD и медиана BE. Найти уравнения AC, BE и BD.

1.27. Найти углы и уравнения сторон треугольника с вершинами A(4;6), B(-3;0) и С(2;-3).

1.28. Найти точку пересечения медиан и точку пересечения высот треугольника, вершины которого A(-4;3), В(2;-4) и С(5;1).

1.29. Найти уравнение прямой, проходящей через начало координат и образующей с прямой у = 2х - 4 угол 45°.

1.30. Найти угол между прямой -2х - Зу +1 = 0 и прямой, проходящей через точки (3;2) и (-4;-5).

1.31. Найти расстояние от точки А(-2,1) до прямой -Зх + 4у – 5 = 0.

1.32. Найти длину высоты AD в треугольнике с вершинами А(3;3), В(-4; 1), С(1;-2).

1.33. Даны уравнения двух сторон квадрата 4х - Зу + 3 = 0, 4х – 3у – 17 = 0 и одна из его вершин А(2;-3). Составить уравнения двух других сторон этого квадрата.

1.34. Составить уравнение прямой, проходящей через точку М(-2;3) на одинаковых расстояниях от точек А(-3 ;7) и В(-5;-1).

1.35. Определить какой из углов, острый или тупой, образованных двумя прямыми х + 3у – 3 = 0 и х - 2у – 2 = 0, содержит начало координат.

1.36. Составить уравнение биссектрисы угла между прямыми х - 2у – –11 = 0 и
Зх + 6у – 5 = 0, в которой лежит точка А(1;-3).

1.37. На прямой у = -2х + 4 найти точку, равноудаленную от точек А(2;-3) и B(-4;1).

1.38. Найти внутренние углы треугольника АВC, если стороны его заданы уравнениями: х + у = 3, 3х – у = 1, x - 3y – 11 = 0.

1.39. Дан треугольник с вершинами А(7;0), В(3;-4), С(2;3). Найти уравнения стороны АВ, высоты CD, биссектрисы BE, медианы CF.