Законы Кирхгофа
Прежде чем составлять систему уравнений на основании законов Кирхгофа, необходимо для заданной схемы выполнить следующее:
1. Подсчитать число ветвей (В) и число узлов (У) схемы;
2. Выбрать произвольно направления токов в ветвях и обозначить токи на схеме;
3. Выбрать на схеме независимые контуры и задаться произвольно направлением обхода в них.

Рис. 10
В данной схеме число ветвей равно семи (В=7). Это ветви ав, ad, ac, вd, вс, cn, nd. В это число не входит ветвь с источником тока, так как по определению источник тока обладает бесконечно большим сопротивлением. Эта ветвь на схеме условно изображена разомкнутой. Показано лишь направление тока от источника тока.
Число узлов в схеме пять (У=5). Это: узлы а, в, c, d, n.
Выберем произвольно направление токов в заданной схеме, например так, как изображено на рис. 10. на данном этапе следует также уточнить, по каким ветвям схемы проходит ток от источника тока. Принципиально нет никакой разницы, как мы зададим направление тока 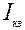 от источника тока: пойдем ли по контуру ncad, т.е. войдём в узел n, далее по ветвям nc, ca, ad и выйдем из узла d или пойдем по контуру ncaвmd, или же войдем в узел n и выйдем из узла d, пройдя только по резистору
от источника тока: пойдем ли по контуру ncad, т.е. войдём в узел n, далее по ветвям nc, ca, ad и выйдем из узла d или пойдем по контуру ncaвmd, или же войдем в узел n и выйдем из узла d, пройдя только по резистору  . Всё это отразиться лишь на уравнениях Кирхгофа. Токи в ветвях от этого не изменятся. С точки зрения удобства расчета и некоторой экономии времени выгоднее всего задать последний путь току
. Всё это отразиться лишь на уравнениях Кирхгофа. Токи в ветвях от этого не изменятся. С точки зрения удобства расчета и некоторой экономии времени выгоднее всего задать последний путь току 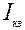 от источника тока, т.е. ток
от источника тока, т.е. ток 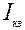 входит в узел n, проходит по резистору
входит в узел n, проходит по резистору  и выходит из узла d. Обозначим этот путь на схеме рис. 10 штриховой линией.
и выходит из узла d. Обозначим этот путь на схеме рис. 10 штриховой линией.
Число неизвестных в заданной схеме, т.е. токов ветвей, равно В.
Первый закон Кирхгофа формулируется следующим образом: алгебраическая сумма токов, сходящихся к любому узлу электрической цепи, равна нулю
 . (18)
. (18)
Токи, подтекающие к узлу, принимают положительными, а утекающие – отрицательными.
Число независимых уравнений К1, которое можно составить по первому закону Кирхгофа, равно числу узлов без единицы:
К1=У-1. (19)
Эти уравнения называются узловыми.
Уравнение для последнего узла не составляется, поскольку его можно вывести из ранее составленных уравнений.
Второй закон Кирхгофа гласит: для любого замкнутого контура электрической цепи алгебраическая сумма всех ЭДС Ек равна алгебраической сумме всех падений напряжений 
 . (20)
. (20)
Падение напряжения принимают положительным, если направление тока через резистор совпадает с направлением обхода контура, а если не совпадает – отрицательным.
Положительными принимают ЭДС, направления действия которых совпадает с направлением обхода контура, и отрицательными – ЭДС, направления действия которых не совпадает с направлением обхода.
По второму закону Кирхгофа можно составить ещё К2 независимых уравнений
К2=В-(У-1)=В-У+1. (21)
Эти уравнения называются контурными.
Контуры следует выбирать таким образом, чтобы в каждый следующий контур входила хотя бы одна новая ветвь. Тогда в К2 независимых контуров будут входить все ветви заданной электрической схемы.
В схеме рис. 10 число узлов У=5. Значит К1=У-1=5-1=4. Составим уравнения по первому закону Кирхгофа для любых четырёх узлов, например, для а, в, с, d:
(а)  ; (22)
; (22)
(в)  ; (23)
; (23)
(с)  ; (24)
; (24)
(d)  . (25)
. (25)
Покажем, что пятое уравнение для узла n будет являться следствием первых четырёх:
(n)  . (26)
. (26)
Сложим уравнения (22) и (23):
 ; (27)
; (27)
 . (28)
. (28)
Подставим (28) в (25):
 . (29)
. (29)
Определим  из (24):
из (24):
 . (30)
. (30)
Подставим в уравнение (29):
 . (31)
. (31)
Умножим обе части на минус единицу:
 . (32)
. (32)
Таким образом, пятое уравнение является следствием первых четырёх.
Контур называется независимым, если в его состав входит хотя бы одна новая ветвь, не входящая в предыдущие контуры. Для сложной разветвлённой схемы можно составить довольно большое число контуров. Так, для схемы рис. 10 можно составить шесть контуров: aвdа, adnса, aвса, aвсndа, adвса, всndв. Независимых контуров всегда значительно меньше. В схеме рис. 3 всего три независимых контура: aвdа, adnса и aвса. Обозначим через Кнк число независимых контуров (Кнк=3).
По формуле (21) найдём число уравнений, которые можно составить по второму закону Кирхгофа:
К2=В-У+1=7-5+1=3.
Следовательно, число уравнений, которые можно составить по второму закону Кирхгофа равно числу независимых контуров (К2= Кнк=3).
Выберем произвольно направления обхода контуров, например, по часовой стрелке, как показано на рис. 10.
Составим уравнения по второму закону Кирхгофа для выбранных независимых контуров:
аdва  ; (33)
; (33)
aвса  ;(34)
;(34)
adnса  . (35)
. (35)
В результате по первому и второму законам Кирхгофа составлены семь уравнений для семи неизвестных токов. Решая их совместно, можно найти значения токов во всех ветвях схемы. Это и будет метод расчёта с использованием законов Кирхгофа.
Подставим в уравнения значения параметров схемы:
 (36)
(36)
Выразим токи  через токи
через токи  с помощью уравнений (22)
с помощью уравнений (22)  (25) и, подставив в уравнения (34) и (35), получим следующую систему уравнений:
(25) и, подставив в уравнения (34) и (35), получим следующую систему уравнений:

Найдём определители этой системы:

 ;
;

 ;
;

 ;
;

 .
.
Найдём токи:

 ;
; 
 ;
;

 ;
;

 ;
;

 ;
;

 ;
;

 .
.
Подстановка полученных токов в уравнение (36) показывает, что выполняются все семь тождеств. Значит, полученные токи являются истинными и мы не сделали ошибки при их вычислении.
Токи  ,
,  ,
,  получились отрицательными. Значит, в действительности токи
получились отрицательными. Значит, в действительности токи  ,
,  и
и  в схеме текут в противоположном направлении.
в схеме текут в противоположном направлении.