Процессы теплопередачи
Возможность достижения требуемого уровня механических свойств и структурного состояния в металле изделий при реализации любого режима термической или комбинированной обработки определяется рядом основных параметров, к которым относятся нагрев и охлаждение (характеризуются температурой нагрева и скоростью изменения температуры металла в определенных температурных интервалах). Операция нагрева во многом определяется процессами перехода тепла от источника энергии (нагревателя) к нагреваемому металлу и передачей тепла внутри металла.
Для правильного понимания сущности параметров термической обработки металлов (далее ТО) целесообразно знать и понимать смысл основных терминов и понятий, рассматриваемых при изучении цикла дисциплин, в т.ч. и «Термическая обработка металлов».
Температура (Т) – является параметром состояния, который характеризует внутреннюю энергию тела. В каждый определенный момент времени для любой точки обрабатываемого металлоизделия характерно только одно значение температуры, которое можно выразить как функцию места (r) и времени (t):
Т=f (r,t);
Рассмотрим процесс передачи тепла обрабатываемому металлоизделию в идеализированном нагревательном устройстве (рис.1.1).

Рис. 1.1 - Схема расположения обрабатываемого изделия в нагревательном устройстве (например, в печи)
1 – нагревательные элементы; 2 – нагреваемое изделие (Соколов К.Н.)
Обрабатываемое металлоизделие с начальной температурой ТК помещается в нагревательное устройство, в котором обеспечивается температура TU. Теплообмен между поверхностью металлоизделия, нагретой поверхностью термического устройства и окружающей изделие средой возможен только при наличии разницы температур (градиента температур - grad t=მt/მх) между ними. Если grad t=0,то тепловой поток отсутствует.
Процесс распространения тепловой энергии от одного тела к другому называется теплопроводностью. При этом перенос тепловой энергии от более нагретого (или участка тела) к менее нагретому телу осуществляется:
- в металлах – путем диффузии свободных электронов (χэ) и с помощью тепловых колебаний решетки, χр (проявляется квантовый характер колебаний при которых энергия переноситсяфононами). Общая теплопроводность равна χобщ=χэ+χр. При этом в чистых металлах обычно χэ<<χр, в высоколегированных кристаллах χэ≈χр, либо даже превышает теплопроводность кристаллической решетки;
- в жидкостях и твердых телах (диэлектриках)- упругими волнами;
-в газах – путем соударения и диффузии атомов или молекул.
Теплопроводность или способность тел пропускать тепло зависит от природы материала и его физического состояния.
Еще в 1853г Видеман и Франц экспериментально установили, что для многих металлов отношение теплопроводности и электропроводности при заданной температуре одинаково. Позднее Лоренц обобщил этот закон и показал, что это отношение пропорционально абсолютной температуре:
χэ=Lo. σ . Т; где Lo-число Лоренца; σ – удельная электропроводность; Т -абсолютная температура.
Закон теплопроводности основан на гипотезе Фурье о пропорциональности теплового потока разности температур на единице длины пути переноса тепла в единицу времени. Общее уравнение теплопроводности Фурье выглядит таким образом: dt/dτ= a + qu/c , g;где:
- a - коэффициент температуропроводности (a=l/с . g);
- qu - удельный тепловой поток;
- с - теплоемкость;
- g - вес единицы объема;
Если величина qu=0, то величина a является единственным параметром, входящим в уравнение теплопроводности. Температуропроводность есть мера инерционности температурного поля в данном материале.
Коэффициент температуропроводности (a,м2\с)характеризует величину временного изменения температуры тела в результате нестационарной теплопроводности и прямопропорционален количеству тепла, передаваемого теплопроводностью, и обратно пропрционален способности металла накапливать тепло (т.е. теплоемкости тела). Чем больший коэффициент температуропроводности имеет тело, тем меньше температурная разность в отдельных местах внутри тела при одинаковых внешних условиях его нагревания или охлаждения. Так, например, для серебра a=0.62 м2/ч; для алюминия a=0.3 м2/ч; для асбеста a=0.00072 м2/ч; для мрамора a=0.002 м2/ч.
Подвод энергии к нагреваемому металлу возможен двумя путями:
- передачей тепла от нагретого тела (нагревателя, например термической печи) к металлу обрабатываемого изделия;
- возникновение тепла непосредственно в обрабатываемом металле за счет контактного подвода и пропускания электрического тока с выделением тепла (джоулевое тепло) или за счет электромагнитной индукции (например, токами высокой частоты – ТВЧ), когда электрическая энергия передается без контакта с нагреваемым телом.
Распределение температуры по всем точкам объема металлоизделия в каждый определенный момент времени называют температурным полем. В более общем случае понятиетемпературного поля охлаждаемого сечения включает значения среднемассовых температур, скорости нагрева и охлаждения по сечению изделия, температурные перепады по сечению и т.д. Температурным полем в объеме называется совокупность мгновенных значений температуры во всех точках рассматриваемого пространства; при этом оно представляется изотермическими поверхностями (рис.1.2), являющимися геометрическим местом точек с одинаковой температурой. Геометрическое место точек с одинаковой температурой называется изотермой.Точки с одинаковой температурой металла лежат на поверхности. Исходя из того, что в одной и той же точке изделия не может быть разных температур, изотермические поверхности не пересекаются. Из этого следует, что изменение температуры металла может происходить только при переходе от одной изотермической плоскости к другой.


А б
Рис. 1.2 – а: направление градиента температуры между двумя изотермическими поверхностями, б: тепловой поток в трубе с двумя изотермическими поверхностями Т и Т±ΔТ
При наличии изменения температуры металла по всем точкам детали в определенный момент времени теплообмен характеризуется нестационарным температурным полем.В том случае, когда изменение температуры металла различных точек по объему детали отсутствует, рассматривается стационарное температурное поле.
Температурное поле внутри тела в любой момент времени можно вычислить решением дифференциального уравнения теплопроводности для определенных начальных и граничных условий (т.е. с учетом конкретных условий процесса с указанием дополнительных данных по геометрической форме тела и его размерах, коэффициента теплопроводности λ,удельной теплоемкостис, плотности r, объемной плотности теплового потока q). Для упрощения теплотехнических расчетов процесса охлаждения на основе теории подобия температурных полей часто вводят безразмерные числа подобия, объединяющие величины, которые оказывают влияние на температурное поле (Q -относительная температура; Bi - число Био; Fo - число Фурье; Ki - число Кирпичева; x\X - относительная координата). В основу теории подобия температурных полей положены (Телегин А.С. и др. Термодинамика и тепломассоперенос. М.: Металлургия, 1980.-264с ) три теоремы:
1.Качественно одинаковые явления имеют одинаковые числа подобия.
2.Любое температурное поле может быть описано числами подобия.
3.Для подобия двух качественно одинаковых явлений достаточно равенства определяющих чисел.
Краевыми условиями называют совокупность граничных и начальных условий (т.е. совокупность дифференциального уравнения теплопроводности и заданных дополнительных условий).
Граничные условия в общем виде отображают условия теплообмена между окружающей средой и поверхностью тела (закон внешнего теплообмена и параметры геометрии тела).
Граничное условие первого рода (первое краевое условие) состоит в задании распределения температуры по поверхности тела в любой момент времени (как функции координат и времени).
Граничное условие второго рода (второе краевое условие) состоит в задании распределения плотности теплового потока на поверхности тела для каждой точки как функции координат и времени.
Граничное условие третьего рода (третье краевое условие) заключается в задании зависимости величины теплового потока вследствие теплопроводности со стороны тела от температур поверхности тела (tПОВ) и окружающей среды (tСР). Для исследования теплового взаимодействия между окружающей средой и поверхностью тела часто используется закон Ньютона :
qПОВ =a(tПов – tСР), где
q – плотность теплового потока, Вт/м2;
tП – температура охлаждаемой поверхности тела, 0С;
tСР – температура охлаждающей среды, 0С.
a - коэффициент пропорциональности, называемый коэффициентом теплопередачи (теплообмена) охлаждающей среды, Вт/м2. 0С. Он характеризует интенсивность теплового взаимодействия среды заданной температуры (tСР) с поверхностью тела. В нестационарных процессах теплообмена температура окружающей среды изменяется во времени.
Плотность теплового потока, подводимого (отводимого) за счет теплопроводности к (или от) поверхности тела, определяется законом Фурье. Поэтому на основании закона сохранения энергии:
- λ ∆t =a(tПов – tСР).
При ТО стальных металлоизделий чаще всего используют граничные условия третьего рода, которые задаются законами взаимодействия между охлаждающей средой и поверхностью тела (закон Ньютона и Фурье). В тех случаях, когда a®¥ (интенсивный теплообмен, при котором температура поверхностных слоев мгновенно снижается до температуры закалочной среды) при расчетах используются граничные условия 1 рода.
Граничные условия четвертого рода(условия сопряжения) соответствуют теплообмену соприкасающихся твердых тел, когда температура соприкасающихся поверхностей одинакова, либо когда происходит теплообмен поверхности тела с окружающей средой (конвективный теплообмен).
Начальные условия – определяются законом распределения температуры внутри тела в начальный момент времени (задаются только при исследовании нестационарного процесса и состоят в задании распределения температуры внутри тела в момент времени, принятом условно за нулевой).
В связи с тем, что распределение температуры в обрабатываемом изделии может исследоваться в объеме, плоскости или линии в литературе различают трёхмерные, двухмерные и одномерные температурные поля.
При рассмотрении двух соседних изотермических плоскостей с различной температурой (рис.1.2а) через любую точку на поверхности одной из них (например точку О) возможно провести только одно направление (линию) которое имеет минимальное расстояние (∆rmin=∆n) до пересечения с изотермической плоскостью с другой температурой (Т+∆Т) и поэтому обладает максимальной разницей по температуре относительно точки О вдоль направления r . Эта величина называется градиентом температуры (grad T) в точке О и представляет собой вектор, направленный перпендикулярно к изотермической плоскости. При повышении температуры он является положительным, а при снижении отрицательным, зависит от места и времени:
grad T= f (r,t);
Разница в тепловой энергии между различными точками металлоизделия выравнивается за счет передачи тепла в течение времени за счет теплового потока (dQ), пропорционального градиенту температуры.
Величина теплового потока (dQ), отнесенная к единице времени (dt) и единице градиента температуры в направлении, перпендикулярном изотер-мической поверхности (dA), называется плотностью теплового потока q.
q= dQ:(dA . dt);
Плотность теплового потока пропорциональна градиенту температуры, который является движущей силой теплового потока:
q = -λ grad T=-λ ∆tпов(это выражение в теплофизике носит названиеуравнения Био-Фурье);где λ – коєффициент теплопроводности (Вт\(м.К);, в качестве коєффициента пропорциональности отражает влияние свойств материала, проводящего тепло, на теплопередачу. Коєффициент теплопроводности характеризует поток тепла, возникающий в металле при наличии градиента температуры, зависит от локального (местного) состояния среды и прежде всего от температуры. Коєффициент теплопроводности численно равен количеству тепла, проходящему через единицу поверхности тела в единицу времени за счет теплопроводности при градиенте температуры, равном единице. В качестве примера приведены значенияλ(Вт/(м,К)для различных материалов при 1000С: сталь 15 для закаленной -53; для отожженной -53; сталь 45 – для закаленной -36; для отожженной -47,8; сталь У8 - для закаленной -28; для отожженной – 46.
Закон Фурье предполагает бесконечно большую скорость распространения теплоты, что можно рассматривать для стационарных процессов и умеренной интенсивности нагрева металла. При исследовании нестационарных процессов с высокой интенсивностью нагрева (например, плазменный нагрев) следует учитывать факт, что теплота распространяется с большой, но ограниченной скоростью.
Изменение температуры нестационарного температурного поля во времени, связанное с передачей тепла в металлоизделии, называется температуропроводностью.
Под теплообменом понимается количество тепла, которым обменивается металлоизделие и окружающая его среда в единицу времени, отнесенное к единице поверхности тела, т.е. количество тепла, которое поступает или уходит из тела в перпендикулярном к его поверхности направлении.
Независимо от способа подвода тепла к обрабатываемому металлу для достижения заданной температуры и выравнивания ее по сечению изделия необходимо время, в течение которого тепло перераспределяется по объему металла за счет теплопроводности и градиента температуры.
Удельный тепловой поток, представленный вектором q,проходит по нормали к единице изотермической поверхности в единицу времени. Вектор теплового потока направлен от больших к меньшим температурам, т.е. в обратную сторону по отношению к grad t. Количество тепла (QU), передаваемого от нагревательного устройства к металлоизделию зависит от материала нагревателя и обрабатываемого изделия, их геометрических размеров и от свойств передающей тепло среды (окружающей нагреваемое тело). Эти характеристики учитываются коэффициентом теплопередачи a (Вт\(м.К). Характеризует собой количество тепла, поглощенного или отданного единицей поверхности в единицу времени при наличии разности температур между телом и окружающей его средой.
За счет теплопередачи в нагреваемом изделии возникает разность температур между поверхностью и центром. В результате теплопроводности с течением времени эта разность температур уменьшается.
При нагреве изделия происходит передача тепла от нагреваемой среды к поверхности металлоизделия (внешний теплообмен)и от поверхностных слоев металлу к внутренним объемам изделия (внутренний теплообмен).
А процесс охлаждения металла при ТО определяется передачей тепла от поверхности нагретого тела в охлаждающую среду (внешний теплообмен) и одновременно от внутренних объемов металла к поверхности (внутренний теплообмен).
Таким образом, внешний теплообмен происходит через поверхность металлоизделия, разграничивающую обрабатываемое изделие и охлаждающую среду. Процесс переноса тепла через единицу поверхности описывается законом Ньютона: q=a(tП – tСР), где
q – плотность теплового потока, Вт/м2;
tП – температура охлаждаемой поверхности тела, 0С;
tСР – температура охлаждающей среды, 0С.
a- коэффициент теплопередачи охлаждающей среды, Вт / м2 . 0С.
Тепловой поток внутри охлаждаемого тела описывается дифференциальным уравнением Фурье. Для тонкого поверхностного слоя металла уравнение принимает вид: q = l dt/dx;где
-l - коэффициент теплопроводности, Вт/м2 0С (ккал/м2 час 0С);
-dt/dx- температурный градиент, 0С/м;
В связи с тем, что тепло, забирающееся охлаждающей средой от нагретого тела и тепло, передающееся от внутренних объемов металла к поверхности, должно быть сбалансировано, то закон Ньютона-Фурье принимает вид:
q = l dt/dx=a (tП – tСР).
При рассмотрении теплотехнических явлений, происходящих при реализации режимов ТО, различают три вида переноса тепла (теплопередачи), отличающиеся друг от друга:
1. Теплопроводность - (или кондукция)- процесс распространения энергии только вследствие взаимодействия структурных частиц вещества (молекул, ионов, атомов и т.д.). Теплопроводность металла является главным внутренним фактором, определяющим скорость нагрева металла. Этот параметр во многом зависит от химического состава материала, степени дефектности металла (табл.1.1). При этом, чем выше содержание углерода и сложнее химический состав металла, тем меньше его теплопроводность, а соответственно должна быть ниже скорость нагрева и охлаждения во избежание возникновения высокого уровня напряжений (для стали с 1% С она в 1,5 раза меньше, чем у стали с 0,2%С). Коэффициент теплопередачи при теплопроводности l (ламбда -греч.)стали в аустенитном состоянии равен 20-25 ккал\м2 час 0С (=*1,163 Вт/м2*С).
Таблица 1.1 – Коэффициенты теплопередачи различных сталей
| Материал | Теплопроводность, Вт/(м2*К) |
| Сталь 20 | |
| Сталь 50 | |
| Сталь У10 | |
| Низколегированная сталь 25ХГС, 30ХН3М, 40Х | |
| Высоколегированные стали: | |
| Р18 | |
| 12Х18Н9 | |
| Г13 | |
| 30Х13 | |
| Чугун серый | |
| Проволока стальная в бунтах | 2,3 |
| Насыпь мелких стальных деталей | 4,7 |
| Стопа тонких стальных листов | 0,58 |
| Окалина | |
| Стружка | 0,8 |
| Никелевый сплав | 12,6 |
| Титановый сплав | 7,2 |
| Алюминиевый сплав | |
| Магниевый сплав |
2. Перемешивание (или конвекция)- процесс переноса теплоты вследствие перемещения относительно больших масс вещества в неоднородном поле температур, что имеет место в движущихся квазисплошных средах (жидкостях, газах, сыпучих и т.д.). Количество передаваемого с помощью конвекции тепла зависит от числа частиц, действующих в качестве передатчиков тепла.
В том случае, когда движение частиц среды обусловлено только разностью в плотностях теплоносителя, вызванной различием температуры, конвекция называется естественной или свободной.
Вынужденной конвекцией называют теплопередачу, осуществляемую с помощью потока теплоносителя, движение которых создается за счет внешних усилий. В общем случае свободная и вынужденная конвекция происходят одновременно и вклад каждого вида конвекции в теплопередачу будет зависеть от градиента температуры в теплоносителе и от скорости принудительного потока.
Коэффициент теплопередачи при конвекции (aк) определяется многими факторами: геометрией и размерами поверхности обрабатываемого металлоизделия; положением изделия в пространстве; физическими свойствами материала; свойствами теплоносителя; причинами возникновения движения теплоносителя (плотность, давление, динамическая вязкость, удельная теплоемкость); разностью температур между обрабатываемым изделием и окружающей средой. На теплопередачу конвекцией влияет также образование паровоздушной (газовоздушной) пленки на границе металл-среда, например при закалке.
3. Теплопередача излучением (радиация) - это процесс переноса энергии, выделившейся из излучающего тела (нагревателя) вследствие теплового движения в веществе, в виде электромагнитных волн через прозрачную (частично или полностью) для них среду. Эти волны в однородной изотропной среде или в вакууме распространяются прямолинейно со скоростью света и подчиняются оптическим законам преломления, поглощения и отражения. Кроме волновых свойств излучение обладает и корпускулярными свойствами, т.е. лучистая энергия испускается и поглощается атомами отдельными порциями – квантами света (фотонами). Энергия фотона равна e=hν;где h = 6,62х10-34 Дж . с(6,62 х10-27эрг.с)-постоянная Планка, ν –частота колебаний эквивалентного электромагнитного поля. Связь νс длиной волны λ определяется соотношением λ . ν=с,где с- скорость света (в вакууме с=3х108 м\с). Для теплопередачи излучением наибольший интерес представляют:
- ультрафиолетовое излучение (λ=0,02…0,4 мкм);
- световое (видимое) излучение (λ=0,4…0,8 мкм);
-инфракрасное(тепловое) излучение (λ=0,8…1000 мкм).
Степень развития этих видов излучения определяется температурой. Для каждой температуры характерен преимущественный вид излучения. Так при температуре твердого тела 1800 К в ультрафиолетовой части спектра излучается всего 0,003% энергии, в световой – 1,6%, а остальная, преимущественная часть энергии излучается в инфракрасной части спектра. Повышение температуры нагревателя приведет к увеличению доли энергии, переносимой излучением в ультрафиолетовой и световой частях спектра. Таким образом, теплообмен излучением связан с двумя стадиями преобразования энергии – на первом этапе внутренняя энергия материала нагревателя преобразуется в энергию фотонов или электромагнитных волн и переносится через среду на поверхность обрабатываемого тема, где она поглощается материалом изделия и преобразуется во внутреннюю или рассеивается.
- теплоемкость (С) - количество теплоты, необходимое для нагрева данного тела на один градус Цельсия, ккал/кг 0С;
- температуропроводность (a) - отношение коэффициента теплопроводности (l)к теплоемкости (С) единицы объема материала, т.е. является функцией теплоемкости, теплопроводности и плотности металла.
a=l/С g,м2/час;
Тепловым потоком(q) называется поток внутренней энергии, самопроизвольно возникающий в вещественной среде с неоднородным температурным полем (обычно направлен из области с высокой температурой в область с пониженной температурой).
Плотность теплового потока, q=a(tП – tСР), где:
q – плотность теплового потока, Вт/м2;
a - коэффициент теплоотдачи охлаждающей среды, Вт/м2 0С; правильно К
tП – температура охлаждаемой поверхности тела, 0С;
tСР – температура охлаждающей среды, 0С.
Количество теплоты, отданное или полученное данной средой (Дж) равно:
Q* = q t= a(TCT-T0) F t (1)
Q* = q t= R(T01-T02) F t (2)
Где: Q* -кол-во теплоты, отданной или полученной данной средой, Дж;
q - тепловой поток, Вт;
TCT- осредненная температура поверхности тела, 0С;
T0 -характерная температура окружающей тело среды, 0С;
T01-T02 -характерные температуры греющей и обогреваемой сред, разделенных перегородкой, , 0С ;
F -площадь поверхности теплообмена, м2;
t - время протекания процесса, с
- теплоотдача- процесс теплообмена (теплопереноса) между средами, разделенными отчетливой границей;
Теплоотдача характеризуется коэффициентомтеплоотдачи (a), Вт\(м2 С) К (или ккал/м2 час 0С), который является множителем пропорциональности в формуле теплообмена;
Величина этого коэффициента зависит от следующих основных факторов: природы нагревающей или охлаждающей среды; температуры среды; циркуляции среды; температуры нагреваемой или охлаждаемой поверхности изделия.
Расчет коэффициентов теплоотдачи для различных периодов охлаждения образца (изделия) в закалочных средах можно производить по формуле:

Где: v -скорость охлаждения в 0С/с; G -вес образца, г; c -теплоемкость, кал\г град.; Δt -разность температур охлаждаемой поверхности образца и среды, 0С; F - охлаждаемая поверхность, см2.
Известно, что коэффициет теплоотдачи (a)охлаждающей среды с изменяющимся агрегатным состоянием зависит от температуры охлаждаемой поверхности металлоизделия. Максимальные значения коэффициента теплоотдачи соответствуют стадии пузырькового теплообмена.
- теплопередачей называют процесс теплообмена между средами, разделенными некоторой перегородкой.
R-коэффициент теплопередачи, Вт/(м2 К)
Величины, обратные этим коэффициентам (1/a и 1/R), называют термическим сопротивлением (Ra)и они равны-Ra= ÑТ/g,где: ÑТ-характерный тепловой напор; g- плотность теплового потока (или тепловое сопротивление -S/l, где S- толщина металла, l - коэффициент теплопроводности металла).
Внешнее термическое сопротивление- сопротивление теплопереносу (при теплоотдаче) от греющей среды к поверхности тела, обратно пропорционально коэффициенту теплоотдачи (1/a), а внутреннее термическое сопротивление, т.е. сопротивление передаче тепла внутри металла (теплопередача), прямо пропорционально толщине нагреваемого металла (L) и обратно пропорционально коэффициенту теплопроводности l (т.е.= L/l).
Отношение внутреннего термического сопротивления к внешнему называетсякритерием Био.Иногда его еще называют критерий конвективно-кондуктивного подобия (число Вио=a.L/l, где a-коэфф.теплоотдачи среды, Вт\(м2.К); l-коэфф.теплопроводности, Вт\(м.К); L-характерный размер изделия, для пластины при одностороннем нагреве таким размером является ее толщина, при двухстороннем –половина толщины, а для цилиндра и шара – радиус).
В связи с тем, что при нагреве металла в печах преобладающим видом теплообмена является излучение, для определения граничных условий между термически тонкими и массивными телами используют еще и радиационное число Старка:
Эти критерии определяют меру термической массивности обрабатываемого изделия (термически тонкое или термически массивное тело).
Понятие критерия Био=a.L/l характеризует отношение внутреннего термического сопротивления к внешнему. Если внутреннее термическое сопротивление материала детали (сопротивление передаче тепла внутри металла от поверхности к глубинным слоям) мало, то скорость нагрева определяется только внешней теплоотдачей (от среды к металлу).
В том случае, если при нагреве металла в печах основным видом теплообмена является излучение, используют для определения границы тонких и массивных тел радиационное число Старка:
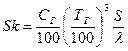

где  - аналог коэффициента теплоотдачи α; Сг- приведенный коэффициент излучения, отнесенный к температуре газов Вт\(м2.К4); Тг-температура газа, К.
- аналог коэффициента теплоотдачи α; Сг- приведенный коэффициент излучения, отнесенный к температуре газов Вт\(м2.К4); Тг-температура газа, К.
При значениях числа Старка Sk ≤0,1…..0,15 тело относится к термически тонкому.
Перепад температур по сечению нагреваемого металла очень мал и такое тело называют условно термически тонким. Это демонстрируется рис 1.3.
Деление обрабатываемых изделий на термически тонкие и массивные является условным и основными факторами, определяющими указанную градацию являются: теплофизические свойства, геометрические размеры и скорость нагрева.
Из рис. 1.3 (б) видно, что скорость охлаждения металла поверхностных слоев и центра цилиндра при охлаждении на воздухе во всем температурном интервале практически не отличаются (кривые охлаждения совпали).
В идеальном случае термически тонким телом называется изделие, скорость нагрева которого подобна скорости нагрева тела из материала с бесконечно большой теплопроводностью (у которой перепад температур по сечению будет равен нулю).
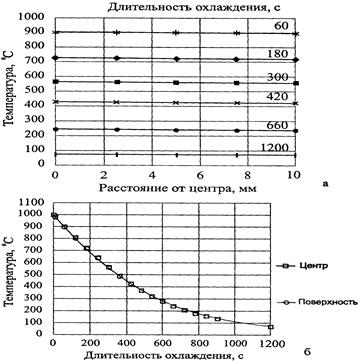
Рис. 1.3 - Температурное поле (а) и кривые охлаждения (б) стального стержня Æ20мм при охлаждении на воздухе с эффективным коэффициентом теплоотдачи среды a=50 Вт\м2.0С (Вi=0,014) [Бояринцева А.В.]
Надо понимать, что термин “термически тонкое тело” имеет не геометрическую характеристику, а теплотехническую. Поскольку даже самое массивное тело можно нагревать (или охлаждать) очень медленно, при этом перепада температур по сечению практически не будет, и такое тело будет относиться к категории термически тонких.
Согласно существующим теплофизическим представлениям при значениях критерия Био менее 0,25 (это соответствует примерно 130-150мм сечения металла) все термообрабатываемые тела относятся к термически тонким. Такие тела можно нагревать практически без ограничения скорости, не опасаясь возникновения опасного уровня напряжений в металле.
Границей перехода от термически тонких к термически массивным телам является значение критерия Био =0,25 (при сохранении перепада температур, равного 0,1, от начальной разности температуры металла и среды).
На рис. 1.4 приведены данные по температурному полю и кривой охлаждения для стального стержня диаметром 20 мм при значении критерия Био>0,25.
При сравнении данных с рис. 1.3 видно перепад температуры по сечению тела и разницу в скорости охлаждения поверхности и центра примерно до температуры металла 2000С (кривые охлаждения сливаются).

Рис. 1.4 - Температурное поле (а) и кривые охлаждения (б) стального стержня Æ20мм при охлаждении в масле с эффективным коэффициентом теплоотдачи среды a=1000 Вт\м2.0С (Вi=0,27) [Бояринцева А.В.]
Для инженерных расчетов рекомендуется [1] границей тонких тел считать значение Био = 0,1, а для расчетов ТО изделий допускается повышение граничного значения до Био=0,3 - 0,4. В области значений критерия Био 0,5>Bi>0,25в металле обрабатываемых изделий появляется более значительная разница (рис. 1.4) между температурой поверхности и центра и изделие считается промежуточным (по термической массивности). Увеличение значений критерия Био до 1,35 (рис. 1.5) существенно увеличивает перепад температур по сечению, который существует при охлаждении тела практически до комнатной температуры. Такое металлоизделие при закалке ведет себя как термически массивное тело.
Такое тело по условиям охлаждения при закалке относится к термически промежуточным (по термической массивности) телам. Дальнейшее увеличение интенсивности охлаждения тела приводит к резкому перепаду скорости охлаждения металла поверхности и центра, начиная практически с момента погружения тела в охлаждающую среду и до окончания охлаждения (рис. 1.6)
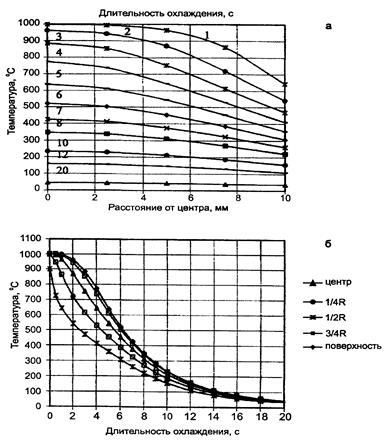
Рис. 1.5 - Температурное поле (а) и кривые охлаждения (б) стального стержня Æ20мм при охлаждении в воде с эффективным коэффициентом теплоотдачи среды a=5000 Вт\м2 . 0С (Вi=1,35) [Бояринцева А.В.]

Рис. 1.6 - Температурное поле (а) и кривые охлаждения (б) стального стержня Æ20мм при охлаждении в воде с эффективным коэффициентом теплоотдачи среды a=100000 Вт\м2 0С (Вi=27) [Бояринцева А.В.]
На практике знание уровня термической массивности обрабатываемого изделия позволяет реализовывать такие кривые нагрева и охлаждения металла, при реализации которых температурный перепад по сечению детали сводится к возможному минимуму и за счет этого снижается уровень внутренних напряжений (термических и структурных), устраняется опасность коробления и растрескивания металла. При нагреве такие технологические приемы сводятся к однократной или многократной остановке нагрева и изотермической выдержке в различных температурных интервалах (в зависимости от хим. состава стали, разнотолщинности изделия и др. факторов) для выравнивания температурного перепада по сечению и снижения уровня образующихся напряжений. При закалке используют различные технологические приемы: охлаждение в двух средах (через воду в масло); изотермическая, ступенчатая и др. режимы закалок.