Аддитивные методы шифрования

Сущность аддитивных методов шифрования заключается в последовательном суммировании цифровых кодов, соответствующих символам исходной информации, с последовательностью кодов, которая соответствует некоторому кортежу символов . Этот кортеж называется гаммой. Поэтому аддитивные методы шифрования называют также гаммированием.

Для данных методов шифрования ключом является гамма. Криптостойкость аддитивных методов зависит от длины ключа и равномерности его статистических характеристик. Если ключ короче, чем шифруемая последовательность символов, то шифртекст может быть расшифрован криптоаналитиком статистическими методами исследования. Чем больше разница длин ключа и исходной информации, тем выше вероятность успешной атаки на шифртекст. Если ключ представляет собой непериодическую последовательность случайных чисел, длина которой превышает длину шифруемой информации, то без знания ключа расшифровать шифртекст практически невозможно. Как и для методов замены в качестве ключа могут использоваться неповторяющиеся последовательности цифр, например, в числах π, е и других.

На практике самыми эффективными и распространенными являются аддитивные методы, в основу которых положено использование генераторов (датчиков) псевдослучайных чисел. Генератор использует исходную информацию относительно малой длины для получения практически бесконечной последовательности псевдослучайных чисел.

Для получения последовательности псевдослучайных чисел (ПСЧ) могут использоваться конгруэнтные генераторы. Генераторы этого класса вырабатывают псевдослучайные последовательности чисел, для которых могут быть строго математически определены такие основные характеристики генераторов как периодичность и случайность выходных последовательностей.

Среди конгруэнтных генераторов ПСЧ выделяется своей простотой и эффективностью линейный генератор, вырабатывающий псевдослучайную последовательность чисел Т(i) в соответствии с соотношением

Т(i+1) = (а * Т(i) + с) mod m,

где а и с - константы, Т(0) - исходная величина, выбранная в качестве порождающего числа.

Период повторения такого датчика ПСЧ зависит от величин а и с. Значение m обычно принимается равным 2^s, где s - длина слова ЭВМ в битах. Период повторения последовательности генерируемых чисел будет максимальным тогда и только тогда, когда с - нечетное число и а (mod 4) = 1 : Такой генератор может быть сравнительно легко создан как аппаратными средствами, так и программно.

Шифр гаммирования

Здесь уделяется внимание получению из ключа программно длинных случайных или псевдо-случайных рядов чисел, называемых на жаргоне отечественных криптографов гаммой, по названию 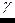- буквы греческого алфавита, которой в математических записях обозначаются случайные величины.

Эти программы, хотя они и называются генераторами случайных чисел, на самом деле выдают детерминированные числовые ряды, которые только кажутся случайными по своим свойствам. От них требуется, чтобы, даже зная закон формирования, но не зная ключа в виде начальных условий, никто не смог бы отличить числовой ряд от случайного.

Можно сформулировать 3 основных требования к криптографически стойкому генератору псевдослучайной последовательности или гаммы:

1. Период гаммы должен быть достаточно большим для шифрования сообщений различной длины.

2. Гамма должна быть труднопредсказуемой. Это значит, что если известны тип генератора и кусок гаммы, то невозможно предсказать следующий за этим куском бит гаммы с вероятностью выше заданной.

3. Генерирование гаммы не должно быть связано с большими техническими и организационными трудностями.

 

Режим гаммирования ГОСТ 28147-89

 

Схема реализации режима гаммирования приведена на рисунке 1.9.

Открытые данные, разбитые на 64-разрядные блоки T₀⁽ⁱ⁾ зашифровываются в режиме гаммирования путем поразрядного суммирования по модулю 2 в сумматоре СМ₅ с гаммой шифра Г_ш⁽ⁱ⁾, которая вырабатывается блоками по 64 бита. Число двоичных разрядов в блоке Т₀^(M), где М определяется объемом шифруемых даных может быть меньше 64, при этом неиспользованная для зашифрования часть гаммы шифра из блока Г_ш^(M) отбрасывается.

В КЗУ вводятся 256 бит ключа. В накопители N₁, N₂ вводится 64-разрядная двоичная последовательность (синхропосылка) S=(S₁,S₂,...,S₆₄), являющаяся исходным заполнением этих накопителей для последующей выработки М блоков гаммы шифра. Синхропосылка вводится в N₁ и N₂ так, что значение S₁ вводится в 1-ый разряд N₁, значение S₃₃ - в 1-ый разряд N₂, S₆₄ - в 32-й разряд N₂.

Исходное заполнение накопителей N₁ и N₂ (синхропосылка S) зашифровывается в режиме простой замены (нижняя часть рисунка). Результат зашифрования A(S)=(Y₀,Z₀) переписывается в 32-разрядные накопители N₃ и N₄ так, что заполнение N₁ переписывается в N₃, а N₂ - в N₄.

Заполнение накопителя N₄ суммируется по модулю (2³²-1) в сумматоре СМ₄ с 32-разрядной константой С₁ из накопителя N₆, результат записывается в N₄.

Заполнение накопителя N₃ суммируется по модулю 2³² в сумматоре СМ₃ с 32- разрядной константой С₂ из накопителя N₅, результат записывается в N₃.

Заполнение N₃ переписывается в N₁, а заполнение N₄ - в N₂. При этом заполнение N₃, N₄ сохраняется.

Заполнение N₁ и N₂ зашифровывается в режиме простой замены. Полученное в результате в N₁, N₂ зашифрование образует первый 64-рарядный блок гаммы шифра Г_ш⁽¹⁾, который суммируется в СМ₅ с первым 64- разрядным блоком открытых данных Т₀⁽¹⁾.

В результате получается 64 - разрядный блок зашифрования данных Г_ш⁽¹⁾.

Для получения следующего 64-разрядного блока гаммы шифра Г_ш⁽²⁾ заполнение N₄ суммируется по модулю (2³²-1) в СМ₄. С константой С₁ из N₆, заполнение N₃ суммируется по модулю 2³² в сумматоре СМ₃ с С₂ (в N₅). Новое заполнение N₃ переписывается в N₁, а новое заполнение N₄ переписывается в N₂., при этом заполнение N_3, N₄ сохраняется.

Заполнение N₁ и N₂ зашифровывается в режиме простой замены. Полученное в результате зашифрования заполнение N₁, N₂ образует второй 64-разрядный блок гаммы шифра Г_ш⁽²⁾, который поразрядно суммируется по модулю 2 в СМ₅ со вторым блоком открытых данных Т₀⁽²⁾.

Аналогично вырабатываются блоки гаммы шифра Г_ш⁽³⁾, ... , Г_ш^(М) и зашифровываются блоки открытых данных Т₀⁽³⁾, ..., Т₀^(М).

В канал связи (или память ЭВМ) передается синхропосылка S и блоки зашифрованных данных Т_ш⁽¹⁾, Т_ш⁽²⁾, ..., Т_ш^(М).

 

Уравнение зашифрования имеет вид:

T_ш⁽ⁱ⁾ = A(Y_i-1 C₂, Z_i-1 ^’C₁) T₀⁽ⁱ⁾ = Г_ш⁽ⁱ⁾ T₀⁽ⁱ⁾,

Где - суммирование по модулю 2³²,

^’ - суммирование по модулю 2³²-1,

- суммирование по модулю 2,

Y_i - содержимое накопителя N₃ после зашифрования i-го блока открытых данных T₀⁽ⁱ⁾;

Z_i - содержимое накопителя N₄ после зашифрования i-го блока открытых данных T₀⁽ⁱ⁾.

(Y₀, Z₀) = A(S).

 

 

Рис.1.9 Режим гаммирования ГОСТ 28147-89

 

Открытое распределение ключей. Схема Диффи-Хеллмана

Важной составной частью шифрсистемы является ключевая система шифра. Под ней понимается описание всех видов ключей (долговременных, суточных, сеансовых и других) и алгоритмов их использования.

Одной из основных характеристик ключа является его размер, определяющий число всевозможных ключевых установок шифра. Если размер ключа чрезмерно велик, то это приводит к удорожанию изготовления ключей, усложнению процедуры установки ключа, понижению надежности работы шифрующего устройства.

Важнейшей частью практической работы с ключами является обеспечение секретности ключа. К основным мерам по защите ключей относятся следующие:

- ограничение круга лиц, допущенных к работе с ключами;

- регламентация рассылки, хранения и уничтожения ключей;

- регламентация порядка смены ключей;

- применение технических мер защиты ключевой информации от несан­кционированного доступа.

Рассмотрим один из принципов распределения ключей (на основе односторонней функции), проработка которого имела весьма неожиданные последствия - была изобретена система шифрования с открытым ключом. Сначала небольшое отступление.

Понятие односторонней функции было введено в теоретическом исследовании о защите входа в вычислительные системы . Функция f(x) называется односторонней (one-way function), если для всех x из ее области определения легко вычислить y=f(x), но нахождение по заданному y₀ такого x₀, для которого f(x₀)=y₀, вычислительно неосуществимо, то есть требуется настолько огромный объем вычислений, что за них просто и не стоит браться.

Однако существование односторонних функций не доказано. В качестве приближения была предложена Гиллом Дж. целочисленная показательная функция f(x)=a^x(mod n), где основание a и показатель степени x принадлежат интервалу (1,n-1), а умножение ведется по модулю n (3*4 mod 10=2; 7*8mod 9=2). Функция вычисляется достаточно эффективно по схеме Горнера. Если представление числа x в двоичной форме имеет вид

x_k-12^k-1 + x_k-22^k-2 + ...+ x₁2¹ + x₀2⁰,

 

то

y = f(x) = a^x mod n = ((...(a^xk-1)²*a^xk-2)²*...*a^x1)²*a^x0 mod n.

Операция, обратная к этой, известна как операция вычисления дискретного логарифма: по заданным y, a и n найти такое целое x, что a^х( mod n) = y. До настоящего времени не найдено достаточно эффективных алгоритмов решения этой задачи.

Американские криптологи Диффи и Хеллман (Diffi W., Hellman M.E. New direction in criptography. IEEE Trans. Inf. Theory, v. IT-22, 1976) предложили схему распространения (рассылки) ключей для секретной связи на основе односторонней показательной функции. Ее суть состоит в следующем.

В протоколе обмена секретными ключами предполагается, что все пользователи знают некоторые числа n и a (1< a < n). Для выработки общего секретного ключа пользователи A и B должны проделать следующую процедуру:

1. Определить секретные ключи пользователей К_А и К_В.

Для этого каждый пользователь независимо выбирает случайные числа из интервала (1,..., n-1).

2. Вычислить открытые ключи пользователей Y_A и Y_B.

Для этого каждый использует одностороннюю показательную функцию Y=a^k mod n со своим секретным ключом.

3. Обменяться ключами Y_A и Y_B по открытому каналу связи.

4. Независимо определить общий секретный ключ К.

Для этого пользователи выполняют вычисления с помощью той же односторонней функции

 

A: Y_B^KA(mod n) = ^[a^{KB ]KA} mod n = a^KA*KB mod n = K.

B: Y_A^KB(mod n) = ^[a^{KA ]KB} mod n = a^KB*KA mod n = K.

Здесь каждый имеет показатель степени, а основание получает от партнера

Безопасность (секретность) изложенной схемы зависит от сложности вычисления секретных ключей пользователей (К_А и К_В). Пока не найдено удовлетворительных быстрых алгоритмов нахождения К из а, Y_A и Y_B без явного определения К_А или К_В.