Расчет характеристик конденсаторов

КОНДЕНСАТОРЫ

Конденсаторы– это компоненты РЭС, способные накап­ливать электрические заряды.

Вопросы для самопроверки

1. Объясните принцип действия конденсатора.

2. Выполните классификацию конденсаторов по различным признакам.

3. Объясните систему обозначений конденсаторов в конструкторской документации.

4. Нарисуйте схемы замещения конденсаторов. Перечислите паразитные параметры конденсатора. Как влияют паразитные параметры на граничную частоту конденсатора?

5. Перечислите основные электрические параметры конденсаторов постоянной и переменной емкости.

6. Объясните механизмы абсорбции и самовосстановления изоляции в конденсаторах.

7. Укажите области применения и приведите основные характеристики низковольтных керамических конденсаторов.

8. Укажите области применения и приведите основные характеристики высоковольтных керамических конденсаторов.

9. Укажите области применения и приведите основные характеристики стеклянных, стеклокерамических и стеклоэмалевых конденсаторов.

10. Укажите области применения и приведите основные характеристики тонкопленочных конденсаторов.

11. Укажите области применения и приведите основные характеристики слюдяных конденсаторов.

12. Укажите области применения и приведите основные характеристики бумажных и металлобумажных конденсаторов.

13. Укажите области применения и приведите характеристики пленочных конденсаторов.

14. Укажите области применения и приведите основные характеристики конденсаторов с оксидным диэлектриком.

15. Объясните устройство и принцип действия различных конденсаторов с оксидным диэлектриком.

16. Объясните принцип действия, укажите области применения и приведите основные характеристики варикапов и варикондов.

17. Нарисуйте схемы контуров с дискретной перестройкой частоты.

 

Примеры решения задач

Расчет характеристик конденсаторов

Пример 3.1.Вывести общий вид выражения для удельной емкости С_уд конденсатора

Решение. Удельная емкость конденсатора рассчитывается по формуле

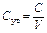, Ф/м³, (3.1)

где V – объем конденсатора, см³.

Если подставить в формулу (3.1) значе­ние объема V = Sd и величину емкости С из (3.2), то получим выражение для удельной емкости конденсатора в виде

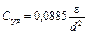, пФ/м². (3.2)

Ответ. 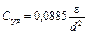пФ/м².

Пример 3.2.Рассчитать реактивную мощность, накопленную в конденсаторе, при следующих исходных данных:

1) емкость конденсатора С=20 мкФ;

2) амплитудное значение пе­ремен­ного напряжения на конденсаторе U=380 В;

3) частота переменного тока f=50 Гц.

Решение. Способность конденсатора накапливать энергию эле­кт­ри­ческого заряда характеризуется реактивной мощ­ностью

Р_х= pfCU², В×А. (3.3)

1. Подставляя значения исходных данных в формулу (3.3), получим

P_x= 3,14∙50∙20∙10^-6∙(380)²=453,4 В∙А.

Ответ. P_x= 453,4 В∙А.

Пример 3.3.Рассчитать допустимую амплитуду переменного напряжения на конденсаторе при следующих исходных данных:

1) допустимая реактивная мощность рассеяния P_{x доп}=100 В·А;

2) емкость конденсатора С=1 мкФ;

3) частота переменного тока f=50 Гц.

Решение.

При эксплуатации конденсаторов на переменном или постоянном токе с наложением переменной составляющей напряжения сумма этих составляющих не должна превышать допустимое напряжение, а амплитуда переменного напряжения, рассчитанного, исходя из до­пу­сти­мой реактивной мощности Р_{х доп.}, не должна превышать значения

U_c = 565×10³ 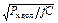, (3.4)

где Р_{х доп}– допустимая реактивная мощность, В·А;f – частота, Гц; С – емкость, пФ.

1. Подставляя исходные данные в формулу (3.4), получаем

U_c=565·10³ 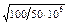=565·10³·1,41·10^-3=796,7 В

Ответ. U_c= 796,7 В.

Пример 3.4.Дана эквивалентная схема конденсатора (рис. 3.1, а), на которой: С – емкость конденсатора; R - сопротивление изоляции; r – сопротивление выводов и обкладок. Вывести выражение для расчета tg δ конденсатора, учитывающее потери в диэлектрике и металле. Постройте (качественно) частотную зависимость tg δ.

Решение.

Пользуясь формулами для перехода от параллельной эквивалентной схемы диэлектрика к последовательной, представим приведенную в условиях задачи эквивалентную схему в виде, изображенном на рис. 3.1, б, где

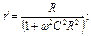
, (3.5)

ω²С ²R²=1/tg²δ_Д; tg δ_Д – тангенс угла потерь рабочего диэлектрика, если считать, что потери в нем обусловлены только сквозной электропроводностью.

Полагая, что tg²δ_Д<<1; ω²С ²R²>>1, получаем

.

Для последовательной схемы

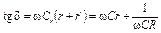. (3.6)

 

Соответствующая полученному выражению частотная зависимость tg δ приведена на рис. 3.1, в.

Пример 3.5.Вывести общий вид выражения R = f(j) для расчета пере­мен­ного радиуса ротора КПЕ согласно рас­чет­ной схеме, представленной на рис. 3.2.

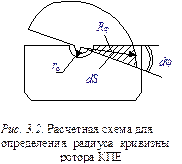Решение. Из схемы, представленной на рис. 3.2, следует, что приращение площади пере­кры­тия dS пластин при повороте подвижных пластин относительно неподвижных на угол dj рассчитывается как разность площадей двух треугольников с высотами R_j и r_o:

dS = 0,5R_j(R_jsindj) – 0,5r_o(r_osindj), (3.7)

где R_j – радиус кривизны ротора; r_o – радиус кривизны выреза на статоре для прохождения оси ротора.

Для малых углов sin dj dj, поэтому выражение для dS можно записать в виде

dS = 0,5R_j² dj – 0,5r_o² dj.

Для перевода углов из радиан в градусы правую часть полученного выражения умножим на p/180. Тогда

dS = (p/360)R_j² dj – (p/360)r_o² dj.

Поделив обе части этого уравнения на dj, получим

. (3.8)

Из формулы (3.8) следует выражение для R_j:

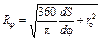. (3.9)

Величину dS/dj в выражении (3.9) найдем из формулы для емкости воздушного конденсатора с плоскими обкладками:

, пФ, (3.10)

где 1,11/4p = e_o – электрическая постоянная, пФ/см; n – число обкладок конденсатора; S – площадь перекрытия обкладок, см²; d – величина зазора между обкладками, см.

Дифференцируя выражение (3.10) по dj, получим, что

, откуда .

Подставляя значение dS/dj в выражение (3.9), окончательно получим

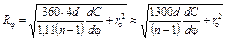. (3.11)

Все линейные размеры в формуле (3.11) выражаются в см, значения емкости в пФ, а углов – в градусах.

Ответ. .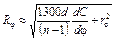

Пример 3.6.Вывести формулу для радиуса кривизны ротора R_j прямо­частотного конденсатора. Рассчитать зависимость R=f(j)и построить развертку профиля пластины ротора при следующих исходных данных:

1)минимальная емкость конденсатора С_min = 15 пФ;

2) максимальный угол разворота ротора j_max = 180°;

3) коэффициент перекрытия контура по частоте k_f = 2;

4) зазор между пластинами ротора и статора d = 0,05 см;

5) количество пластин ротора n = 6;

6) радиус выреза на пластине ротора r_o = 0,3 см.

Решение. Функциональная характеристика для КПЕ с вращательным перемещением ротора C = f(j), где j – угол поворота оси конденсатора. Вид функциональной характеристики задается специальной формой пластин ротора или статора. Как правило, минимальному углу разворота ротора j = 0 соответствует минимальная емкость КПЕ, C_min, а максимальному углу j_max соответствует значение максимальной емкости КПЕ С_max. Обычно j_max = 180°.

Практически важными являются следующие функциональные характеристики КПЕ.

Прямоемкостная функциональная характеристика пред­­ставляет линейную зависимость емкости КПЕ от угла поворота ротора.

C = , пФ. (3.12)

где k_с = С_max/C_min – коэффициент перекрытия по емкости; k_f = - коэффициент перекрытия по частоте.

График зависимости (3.12) показан на рис. 3.3 (кривая 1).

Прямоволновая функциональная характеристика пред­ставляет собой квадратичную зависимость емкости конденсатора от угла поворота ро­тора:

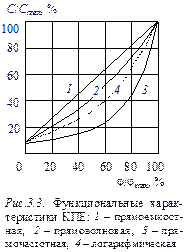
. (3.13)

График функции (3.13) представлен на рис. 3.3 (кривая 2).

Прямочастотная функци­о­­­нальная ха­рактеристика представляет собой обратную квадратичную зависимость емкости конденсатора от угла поворота ро­тора:

. (3.14)

График функции (3.14) изображен на рис. 3.3 (кривая 3).

Логарифмическая функцио­на­ль­ная характеристикапред­став­­ляет экс­поненциальную зависи­мость емко­сти КПЕ от угла поворота ротора:

С = ae^bj, пФ, (3.15)

где a=C_min, пФ; b = 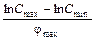= = , 1/град.

График функции (3.15) изображен на рис. 3.3 (кривая 4).

1. Дифференцируя выражение (3.14) по j, получим, что

.

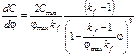Подставляя это значение в формулу (3.1), получим значение R_j в виде:

. (3.16)

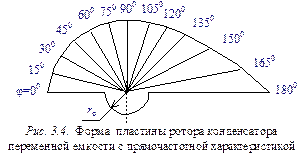
2. При определении радиуса кривизны R_j пластины ротора воспользуемся выражением (3.48) и рассчитаем значения R_j прямочастотного КПЕ для углов j = 0; 15°; 30°; 45°; 60°; 75°; 90°; 105°; 120°; 135°; 150°; 165°; 180°. Результаты расчетов приведены в таблице 3.1. Эскиз расчета профиля развертки пластины представлен на рис. 3.4.

Таблица 3.1

Результаты расчета радиуса кривизны пластины ротора прямочастотного конденсатора переменной емкости
j, °
Rj,см	1,08	1,15	1,22	1,31	1,40	1,51	1,64	1,78	1,95	2,15	2,38	2,65	2,96

 

Пример 3.7.Рассчитатьмаксимальную емкость С_min и коэффициент перекрытия по емкости к_С КПЕ со следующими параметрами:

1) рабочий диапазон частот от f_min = 5 МГц до f_max = 10 МГц;

2) минималь­ная емкость С_min = 15 пФ;

3) постоянная емкость элементов схемы С₀=20 пФ.

Решение.

1. Рассчитываем коэффициент перекрытия диапазона по формуле

.

2. Максимальная емкость C_max КПЕ рассчитывается по формуле

C_max = (C_min+C_o) k_f² – C_o, (3.17)

где С_о 20¼25 пФ – постоянная емкость элементов схемы контура (входные емкости транзисторов, емкость монтажа, паразитная емкость контурной катушки) при отключен­ном КПЕ.

Полагая С_о = 20 пФ и подставляя значения C_min и k_f в формулу (3.17), получим, что

C_max = (15 + 20)4 - 20 = 120 пФ.

3. Коэффициент перекрытия по емкости КПЕ рассчитывается по формуле

.

Таким образом, учет значения емкости С_о в реальном колебательном контуре показывает, что k_С 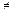k_f².

Ответ. C_max = 120 пФ; k_C=8.

Пример 3.8.Определить значение тангенса угла потерь КПЕ для минимальной частоты настройки колебательного контура при следующих исходных данных:

1) минимальная частота контура f_min = 5×10⁶ Гц;

2) максимальная емкость КПЕ С_max составляет 120 пФ = 1,2×10^–10 Ф

3) сопротивление последовательных потерь в металлических частях конденсатора r = 0,1 Ом

4) сопротивление параллельных потерь R 10¹² Ом;

5) тангенс угла потерь вспомогательных диэлектриков tgd_всп =10^–4.

Решение.

1. Полный тангенс угла потерь КПЕ с воздушным диэлектриком складывается из трех составляющих:

tgd = tgd₁ + tgd₂ + tgd₃, (3.18)

где tgd₁ = wCr – cоставляющая угла потерь, обусловленная последовательными потерями в металлических частях конденсатора; С – текущая емкость конденсатора; tgd₂ = – составляющая тангенса угла потерь, обусловленная потерями во вспомогательных диэлектриках; С_вспi, tgd_вспi– емкости и тангенсы угла потерь вспомогательных диэлектриков, используемых в конструкции КПЕ; С_min– минимальная емкость конденсатора, причем 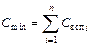; tgd₃ = 1/wCR – составляющая тангенса угла потерь, обусловленная поверхностными утечками и потерями в воздушном диэлектрике, оксидном слое и поверхности пластин (параллельными потерями).

2. Рассчитаем по формуле (3.18) значение тангенса угла потерь КПЕ. При расчетах принимаем, что тангенс угла потерь вспомогательных диэлектриков tgd_всп = tgd₂. В результате получаем суммарный тангенс угла потерь КПЕ равным:

tgd = 6,28×5×10⁶×1,2×10^–10×0,1 + 10^–3 + 1/(6,28×5×10⁶×1,2×10^–10×10¹²) =

= 3,77×10^–4+10^–4 + 2,65×10^–10 5×10^–4.

Анализируя полученное выражение, приходим к выводу, что основное вли­яние на тангенс угла потерь КПЕ оказывают последовательные потери tg d₁ = 3,77×10^–4 в металлических частях конденсатора (в обкладках и токосъеме).

Ответ. tgd 5×10^–4.