Примеры решения задач
ЗАДАЧА 1. Пространство между обкладками плоского конденсатора заполнено без зазора двумя слоями диэлектриков, параллельными пластинам. Первый слой – фарфор толщиной d1 = 2 мм, второй – эбонит толщиной
d2 = 1,5 мм. Определить емкость C такого конденсатора, если площадь пластин S = 100 см2.
| ДАНО: d1 = 0,002 м d2= 0,0015 м S = 0,01 м2 |
| С – ? |
АНАЛИЗ. Для решения задачи представим конденсатор с диэлектриками как два последовательно соединенных конденсатора. Напряжение на конденсаторе равно U = U1+U2, где U1 и U2 – напряженияна слоях диэлектрика. Чтобы найти емкость конденсатора С, необходимо знать U1 и U2. Для этого следует воспользоваться связью напряженности и потенциала и условиями на границе раздела двух диэлектриков, а также учесть, что нормальная составляющая вектора смещения 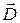 при переходе через границу не меняется.
при переходе через границу не меняется.
РЕШЕНИЕ. Емкость конденсатора равна C = q/U = q/(U1+U2 ), (2.3.1)
где q – заряд пластины (рис. 2.3.1).
 Поле внутри конденсатора однородно, поэтому связь напряженности и потенциала дает
Поле внутри конденсатора однородно, поэтому связь напряженности и потенциала дает
U1 = E1d1, U2 = E2d2; поэтому 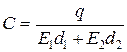 .
.
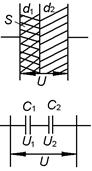 Рис. 2.3.1
Рис. 2.3.1
|
Вектор напряженности связан с вектором электрического смещения соотношением 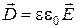 или
или 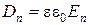 .
.
Поскольку 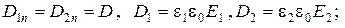
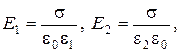

где 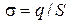 – поверхностная плотность заряда, получаем
– поверхностная плотность заряда, получаем
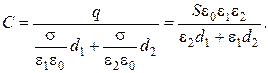
Проверим размерность: 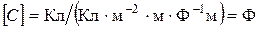 .
.
Подставив значения, получаем: 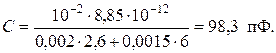
ОТВЕТ: С = 98,3 пФ.
ЗАДАЧА 2. Два плоских конденсатора одинаковой электроемкости (C1 = C2) соединены в батарею последовательно и подключены к источнику тока с электродвижущей силой 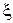 . Как изменится разность потенциалов U1 на пластинах первого конденсатора, если пространство между пластинами второго конденсатора, не отключая источника тока, заполнить диэлектриком с диэлектрической проницаемостью e = 7 (рис. 2.3.2)?
. Как изменится разность потенциалов U1 на пластинах первого конденсатора, если пространство между пластинами второго конденсатора, не отключая источника тока, заполнить диэлектриком с диэлектрической проницаемостью e = 7 (рис. 2.3.2)?
ДАНО:
C1 = C2; U1 = const
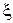 ; e = 7 ; e = 7
|
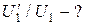
|
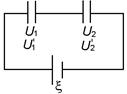 AНАЛИЗ. До заполнения второго конденсатора диэлектриком разность потенциалов на пластинах обоих конденсаторов была одинакова
AНАЛИЗ. До заполнения второго конденсатора диэлектриком разность потенциалов на пластинах обоих конденсаторов была одинакова
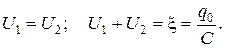
После заполнения источник тока не отключался, поэтому общая разность потенциалов на батарее конденсаторов осталась прежней, 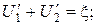 она лишь перераспределилась между конденсаторами. Учитывая, что емкость второго конденсатора увеличилась в e раз, можно найти новую разность потенциалов на первом конденсаторе
она лишь перераспределилась между конденсаторами. Учитывая, что емкость второго конденсатора увеличилась в e раз, можно найти новую разность потенциалов на первом конденсаторе 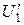 .
.
РЕШЕНИЕ. После заполнения диэлектриком разности потенциалов на конденсаторах стали равны
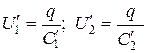 , (2.3.2.)
, (2.3.2.)
где q – заряд обкладки конденсатора,q¹q0 , 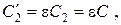 электроемкость первого конденсатора не изменилась, C1¢ = C1 = C.
электроемкость первого конденсатора не изменилась, C1¢ = C1 = C.
Поскольку при последовательном соединении конденсаторов заряд на каждой пластине и на всей батарее одинаков, то 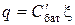 , где
, где 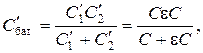
тогда 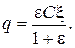 (2.3.3)
(2.3.3)
Подставив (2.3.3) в (2.3.2), получим 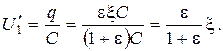
Искомое отношение равно 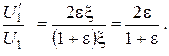
Правильность формулы по размерности очевидна. Подставив значения, получаем 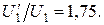
ОТВЕТ: 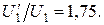
ЗАДАЧА 3. Радиус центральной жилы коаксиального кабеля 1,5 см, радиус оболочки 3,5 см. Между центральной жилой и оболочкой приложена разность потенциалов 2300 В. Вычислить напряженность электрического поля на расстоянии 2 см от оси кабеля.
ДАНО:
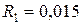 м м
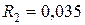 м
U = 2300 В
r = 0,020 м м
U = 2300 В
r = 0,020 м
|
| Е – ? |
АНАЛИЗ. Кабель можно уподобить цилиндрическому конденсатору. Электрическое поле создается только центральной жилой. Напряженность этого поля следует определять как напряженность поля бесконечной заряженной нити.
РЕШЕНИЕ. Напряженность поля кабеля равна
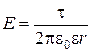 .(2.3.4)
.(2.3.4)
Кабель заряжен равномерно, поэтому t= q/ 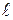 .
.
Заряд можно определить, если известна емкость конденсатора C, q = CU0, тогда t= CU0/ 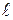 . (2.3.5)
. (2.3.5)
Известно, что емкость цилиндрического конденсатора определяется по формуле: 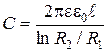 (2.3.6)
(2.3.6)
Используя выражения (2.3.5) и (2.3.6) получаем 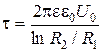 . (2.3.7)
. (2.3.7)
Подставим (2.3.7) в равенство (2.3.4): 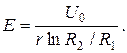
Правильность формулы по размерности очевидна. Подставив значения, получаем
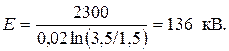
ОТВЕТ: 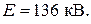
ЗАДАЧА 4. Плоский воздушный конденсатор с площадью пластины S = 500 см2, подключен к источнику тока, ЭДС которогоξ = 300 В. Определить работу А внешних сил по раздвижению пластин от расстоянияd1 = 1 см доd2 = 3 см в двух случаях: а) пластины перед раздвижением отключаются от источника тока; б) пластины в процессе раздвижения остаются подключенными к нему.
| ДАНО: ξ = 300 В d1 = 0,01 м d2 = 0,03 м S = 0,05 м2 |
| А – ? |
АНАЛИЗ. В первом случае систему двух заряженных и отключенных от источника тока пластин можно рассматривать как изолированную систему, по отношению к которой справедлив закон сохранения энергии. В этом случае работа внешних сил равна изменению энергии системы 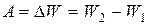 , где W2 – энергия поля конденсатора в конечном состоянии (с расстоянием между пластинамиd2), W1 – энергия поля конденсатора в начальном состоянии(d = d1).
, где W2 – энергия поля конденсатора в конечном состоянии (с расстоянием между пластинамиd2), W1 – энергия поля конденсатора в начальном состоянии(d = d1).
Во втором случае пластины остаются подключенными к источнику тока, и система двух пластин уже не является изолированной (заряд пластин при их раздвижении перемещается к клеммам батареи). Разность потенциалов при раздвижении пластин остается неизменной U = ξ. В этом случае 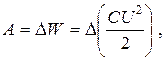 причем U = const,а C меняется. Емкость плоского конденсатора C = e0S/d будет уменьшаться, следовательно, будет уменьшаться заряд на пластинах, q = CU, и напряженность поля конденсатора E = U/d.
причем U = const,а C меняется. Емкость плоского конденсатора C = e0S/d будет уменьшаться, следовательно, будет уменьшаться заряд на пластинах, q = CU, и напряженность поля конденсатора E = U/d.
В этом случае работу вычислим как интеграл 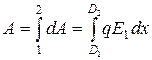 , (2.3.8)
, (2.3.8)
где E1 – напряженность поля, создаваемого зарядом одной пластины.
РЕШЕНИЕ. В первом случае заряд q каждой из пластин, отключенных от источника, при их раздвижении не меняется, q = C1x .
Энергия электрического поля конденсатора равна 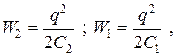
поэтому 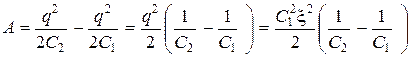 . (2.3.9)
. (2.3.9)
Электроемкости равны соответственно 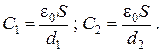 (2.3.10)
(2.3.10)
Подставив (2.3.10) в (2.3.9), получаем 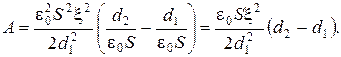
Проверим размерность: 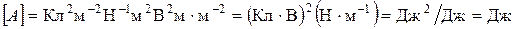 .
.
Подставив значения, получаем 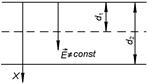
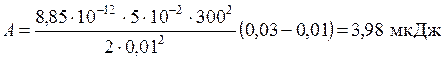 .
.
Рассмотрим второй случай.
Выразим напряженность E1 поля и заряд q через расстояние х между пластинами (рис. 2.3.3).
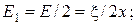 (2.3.11)
(2.3.11)
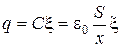 . (2.3.12)
. (2.3.12)
Подставив выражения (2.3.11) и (2.3.12) в формулу(2.3.8), получаем
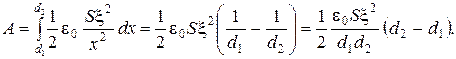
Проверим размерность: 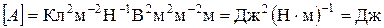 . Подставив значения, получаем
. Подставив значения, получаем
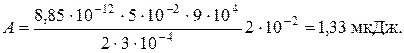
ОТВЕТ: 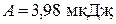
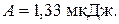
ЗАДАЧА 5. Плоский конденсатор заряжен до разности потенциаловU = 1 кВ. Расстояние между пластинамиd = 1 см, диэлектрик – стекло. Определить объемную плотность энергии конденсатора.
| ДАНО: U = 1000 В d = 0,01 м ε = 7 |
| w – ? |
АНАЛИЗ И РЕШЕНИЕ.
Объемная плотность энергии конденсатора вычисляется по формуле 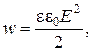
причем напряженность поля плоского конденсатора E = U/d поэтому 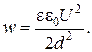
Проверим размерность: 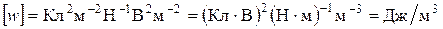 . Подставив значения, получаем:
. Подставив значения, получаем: 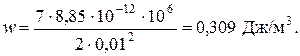
ОТВЕТ: 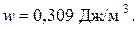
ЗАДАЧА 6. Металлический шар радиусом R = 3 см несет заряд 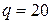 нКл. Шар окружен слоем парафина толщиной d = 2 см. Определить энергию W электрического поля, заключенного в слое диэлектрика.
нКл. Шар окружен слоем парафина толщиной d = 2 см. Определить энергию W электрического поля, заключенного в слое диэлектрика.
ДАНО:
R = 0,03 м
ε = 2
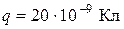 d = 0,02 м
d = 0,02 м
|
| W – ? |
АНАЛИЗ. Поле, созданное заряженным шаром, является неоднородным, поэтому энергия поля в слое диэлектрика распределена неравномерно. Однако объемная плотность энергии будет одинакова во всех точках, отстоящих на равных расстояниях от центра сферы, т. к. поле заряженного шара обладает сферической симметрией (рис. 2.3.4). Энергия в элементарном сферическом слое диэлектрика объемом dV равна 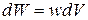 , гдеw – объемная плотность энергии.
, гдеw – объемная плотность энергии.
 Полная энергия равна интегралу
Полная энергия равна интегралу  .
.
РЕШЕНИЕ. Учитывая, что dV = 4p r2d r, где r – радиус элементарного сферического слоя толщиной  , получаем
, получаем 
Объемная плотность энергии определяется выражением  ,
,
причем напряженность поля E в сферическом слое диэлектрика радиусом r равна  .
.
Тогда 

Проверим размерность:  . Подставив значения, получаем:
. Подставив значения, получаем:  ОТВЕТ:
ОТВЕТ: 