Распределение носителей в зонах

Концентрация носителей в ЗП и в ВЗ зависит от плотности потенциальных уровней Р(j) и от вероятности нахождения электронов на этих уровнях. Как известно из физики,

где а – физическая константа, равная , m_эф – эффективная масса электрона или дырки, h – постоянная Планка, равная 6,6×10^-34 Дж×с; φ_гр– граничный потенциал зоны проводимости или валентной зоны..

Вероятность нахождения электронов на том или ином уровне согласно распределительному закону Ферми-Дирака может быть определена следующим образом:

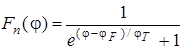где φ– потенциал, на котором находится электрон; j_Т – температурный потенциал; φ_F – потенциал уровня Ферми или просто уровень Ферми. Это такой потенциал, вероятность нахождения электрона на котором равна 0,5.

Уровень Ферми в большинстве полупроводников находится внутри ЗЗ. Раз это так, то разница (φ – φ_F) >> φ_T, т.к. φ_T » 0,025 В, поэтому можно пренебречь единицей и записать .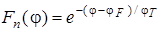

Вероятность нахождения дырки в ВЗ равна вероятности отсутствия электрона.

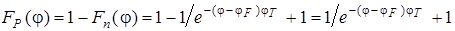Поскольку

тогда

Концентрация электронов в зоне проводимости может быть найдена как интеграл от произведения вероятности нахождения электрона в ЗП F_n(j) и плотности потенциальных уровней Р_п(j). Пределы интегрирования от границы j_c до ¥.

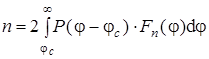Множитель 2 означает, что на одном потенциальном уровне может находиться два электрона. Подставив значения Р(j – j_c) и F_n(j), получим

Решим интеграл методом замены переменных. Примем 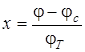, тогда

; ;

;

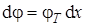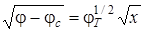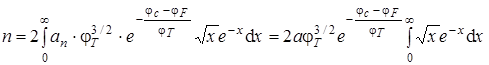Интеграл от 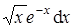является табличным и равен 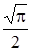, тогда

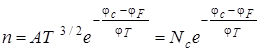, (1.1)

где – постоянный коэффициент; 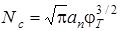– эффективная плотность уровней в зоне проводимости.

Вывод 1: концентрация электронов в зоне проводимости зависит от температуры и разницы потенциалов 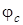и 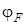. Чем выше температура и меньше разница, или что тоже, больше концентрация примеси донора, тем больше электронов в зоне проводимости, и, следовательно, выше электропроводность полупроводника.

Аналогично можно найти концентрацию дырок в валентной зоне

или, подставляя значения плотности и вероятности, получим

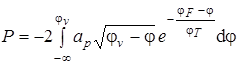Произведем замену переменных, обозначив через , тогда 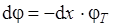, , а пределы интегрирования от 0 до +¥.

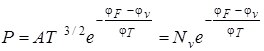, (1.2)

где 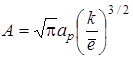– постоянный коэффициент; 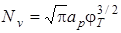– эффективная плотность уровней в валентной зоне.

Вывод 2: концентрация дырок в валентной зоне зависит от температуры и разнице потенциалов 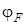и . Чем выше температура и меньше разница, или что тоже, больше концентрация акцепторной примеси, тем больше дырок в валентной зоне, а, следовательно, выше электропроводность полупроводника.

Для анализа проводимости собственных полупроводников (без примеси) найдем произведение концентраций электронов и дырок. Из формул (1.1) и (1.2)

Следовательно, произведение концентраций при постоянной температуре не зависит от 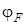, а определяется лишь шириной запрещенной зоны.

Так как в собственных полупроводниках

то

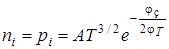Отсюда можно сделать вывод, что собственная концентрация определяется лишь шириной запрещенной зоны и сильно зависит от температуры.

Произведение концентраций n и р в любом типе полупроводника есть величина постоянная при постоянной температуре и может быть найдена как

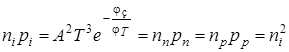, (1.3)

где 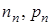– концентрация электронов и дырок в n-полупроводнике; 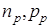– концентрация электронов и дырок в р-полупроводнике; 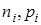– концентрация электронов и дырок в собственном полупроводнике.