Алгоритмизация вычислительных процессов

Алгоритмом называется совокупность правил, определяющих данный вычислительный процесс, которыйот исходных данных за конечное число шагов (этапов, действий, операций) приводит к искомому результату. Решить задачу – значит найти ее алгоритм. Любому алгоритму присущи следующие свойства:

· Дискретность – процесс решения задачи разбивается на отдельные этапы (шаги).

· Детерминированность – любое правило преобразования данных на любом шаге должно выполняться однозначно.

· Результативность – применение алгоритма к исходным данным за конечное число шагов должно привести к результату (конечность алгоритма). Отсюда следствие: бесконечных алгоритмов не существует.

· Массовость – алгоритм служит для решения не одной задачи, а целого класса задач (универсальность алгоритма).

Все многообразие вычислительных алгоритмов включает в себя в виде фрагментов 3 типовых вычислительных процесса:

· Линейный – последовательность операций, выполняемых одна за другой.

· Ветвящийся – выполнение операций по одному из возможных направлений (ветвей алгоритма) в зависимости от некоторых условий.

· Циклический – многократное выполнение некоторых операций в соответствии с заданным условием окончания цикла.

Описание алгоритма задачи может быть задано разными способами:

· Словесный – запись инструкций по выполнению алгоритма на естественном языке.

· Графический – представление алгоритма с использованием геометрических символов в виде блок-схем, граф-схем.

· Формализованный – описание алгоритма на одном из искусственных языков высокого уровня (ЯВУ) в виде последовательности строго определенных инструкций по обработке данных.

· Программный – запись алгоритма на языкеЭВМ в виде последовательности ее команд.

С целью наглядного представления процесса решения задачи используются схемы алгоритмов, которые составляются в соответствии с требованиями ГОСТ «Единая система программной документации» (ЕСПД) – ГОСТ 19.701-90 «Схемы алгоритмов, программ, данных и систем». Символы в схеме алгоритма могут обозначаться идентификаторами (или номерами) слева над символом.

Рассмотрим основные графические символы (блоки), используемые для представления алгоритмов:

Символ	Наименование	Выполняемые функции
	Терминатор	Начало или конец схемы алгоритма
	Данные	Ввод данных или вывод результатов
	Процесс	Обработка данных любого вида
	Решение	Разветвление алгоритма после проверки условия, записанного внутри символа
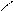
	Границы цикла	Начало и конец цикла, с условиями продолжения в начале для цикла с предусловием или в конце для цикла с постусловием, с указанием параметра цикла в обоих блоках
	Предопределен- ный процесс	Обращение к подпрограмме, описанной в другом месте
	Линия	Линии потока данных или управления (слева направо и сверху вниз без стрелок)
	Соединитель	Обрыв линии потока и продолжение ее в другом месте с общим обозначением
	Комментарий	Пояснительные записи (объяснения, примечания) к символу или группе символов, обведенных пунктирной линией