Построение модели
Задача четко поставлена, теперь нужно сформулировать для нее математическую модель. Это очень важный шаг в процессе решения, и его надо хорошо обдумать. Выбор модели существенно влияет на остальные этапы в процессе решения.
Как вы можете догадаться, невозможно предложить набор правил, автоматизирующих стадию моделирования. Большинство задач должно рассматриваться индивидуально. Тем не менее, существует несколько полезных руководящих принципов. Выбор модели - в большей степени дело искусства, чем науки, и, вероятно, эта тенденция сохранится. Изучение удачных моделей - это наилучший способ приобрести опыт в моделировании.
Для математической модели можно дать такое определение - это совокупность математических зависимостей, описывающих функционирование объекта.
Математические модели могут быть получены теоретическим и экспериментальным путем. Однако на практике математическая модель объекта чаще всего получается при сочетании теоретических и практических методов.
Наиболее общие правила построения моделей можно сформулировать таким образом:
1. Выяснение физической природы объекта и составление принципиальной физической картины его функционирования.
2. Запись основных положений физического представления с помощью математических соотношений.
3. Упрощение математических соотношений с использованием огрубления, пренебрежения второстепенными факторами и т.п.
Следует отметить, что 2 и 3 пункт часто очень трудно разделить между собой, так как подчас сформулировать математически задачу бывает невозможно без соответствующих упрощений и огрублений. Иногда построение математической модели идет не по пути «от сложных математических преобразований к простым», как показано выше, а, наоборот, от простых математических форм к более сложным. И, наконец,
4. После создания математической модели целесообразно провести исследования на ее ограничения и область применения.
Если ограничения и область применения математической модели не удовлетворяют реальной физической картине функционирования объекта, то необходимо пересмотреть п.3, 2, а возможно и 1.
С практической точки зрения для однозначного определения математической модели в ряде случаев полезно составить некоторые дополнительные или вспомогательные программы, в которых необходимо рассмотреть правильность модели, ее ограничения и упрощения.
Отметим и еще одну особенность составления математических моделей - приступая к ее разработке, следует задать, по крайней мере, два основных вопроса:
1. Какие математические структуры больше всего подходят для задачи?
2. Существуют ли решенные аналогичные задачи?
Второй вопрос, возможно, самый полезный во всей математике. В контексте моделирования он часто дает ответ на первый вопрос. Действительно, большинство решаемых в математике задач, как правило, являются модификациями ранее решенных. Большинство из нас просто не обладает талантом Ньютона, Гаусса или Эйнштейна, и для продвижения вперед нам приходится руководствоваться накопленным опытом.
Сначала нужно рассмотреть первый вопрос. Мы должны описать математически что мы знаем и что хотим найти. На выбор соответствующей структуры будут оказывать влияние такие факторы, как:
1) ограниченность наших знаний относительно небольшим количеством структур,
2) удобство представления,
3) простота вычисления,
4) полезность различных операций, связанных с рассматриваемой структурой или структурами.
Сделав пробный выбор математической структуры, задачу следует переформулировать в терминах соответствующих математических объектов. Это будет одна из возможных моделей, если мы можем утвердительно ответить на такие вопросы, как:
Вся ли важная информация задачи хорошо описана математическими объектами?
Существует ли математическая величина, ассоциируемая с искомым результатом?
Выявили мы какие-нибудь полезные отношения между объектами модели?
Можем мы работать с моделью? Удобно ли с ней работать?
Для лучшего понимания вопросов составления модели, рассмотрим транспортную задачу, которую мы формулировали выше, когда составляли ТЗ.
Пример. Возвращаемся к задаче агента по продаже компьютеров, рассмотренной ранее в этом разделе. Начинаем с постановки задачи, данной в конце примера.
Решали ли мы ранее аналогичные задачи? В математическом смысле, вероятно, нет. Однако все мы сталкивались с задачами выбора пути по дорожным картам или в лабиринтах. Можем ли мы прийти к удобному представлению нашей задачи наподобие карты?
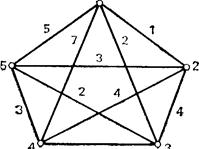
Очевидно, нужно взять лист бумаги и нанести на нем по одной точке, соответствующей каждому городу. Мы не собираемся изображать точки так, чтобы расстояние между каждой парой точек, соответствующих городам i и j, было пропорционально стоимости проезда Cij. Расположим точки любым удобным способом, соединим точки i и j линиями и проставим на них «веса» Cij.
Схема, которую мы только что изобразили,— это частный случай известного в математике графа, или сети. В общем случае сеть — это множество точек (на плоскости) вместе с линиями, соединяющими некоторые или все пары точек; над линиями могут быть проставлены веса.
|
Г о р о д а
1 2 3 4 5
1 - 1 2 7 5
2 1 - 4 4 3
3 2 4 - 1 2
4 7 4 1 - 3
5 5 3 2 3 -
а б
Рис. 3.2. Задача коммивояжера с пятью городами
Для простоты предположим, что у Виктора только пять городов, для которых матрица стоимостей показана на рис. 3.2 a. Тогда сетевая модель может быть изображена, как на рис. 3.2 б. Предположим также, что стоимость проезда из города i в город j такая же, как и из j в i, хотя это и необязательно.
Что мы ищем в задаче? В терминах теории сетей список городов (который мы ранее описали) определяет замкнутый цикл, начинающийся с базового города и возвращающийся туда же после прохождения каждого города но одному разу. Такой цикл соответствует неотрывному движению карандаша вдоль линий сети, которое проходит через каждую точку только одни раз и начинается и оканчивается в одной и той же точке. Обход такого рода назовем туром. Стоимость тура определяется как сумма весов всех пройденных ребер. Задача решена, если мы можем найти тур с наименьшей стоимостью.
Па рис. 3.2, обход 1—5—3—4—2—1 есть тур со стоимостью 5+2+1+4+1=13. Является ли он туром с минимальной стоимостью? Рассмотренная задача известна в литературе как задача коммивояжера, она стала в какой-то мере классической. Это один из наиболее известных примеров таких задач, которые очень легко поставить и промоделировать, по очень трудно решить. Время от времени мы будем возвращаться к этой задаче в целях иллюстрации.