Кривые безразличия. Предельные полезности и предельные нормы замещения товаров

Предельной полезностью товара вида i называется частная производная .

Кривой безразличия для данного набора товаров называется геометрическое место точек , которые находятся в отношении безразличия с этим набором х, то есть множество .

Уравнение кривой безразличия имеет вид:

. (1.2.1)

Множество кривых безразличия называется картой кривых безразличия.

Кривые безразличия обладают следующими свойствами:

1. Кривые безразличия, соответствующие разным уровням удовлетворения потребностей, не касаются и не пересекаются (из условия транзитивности).

2. Кривые безразличия убывают (из условия ненасыщаемости). Исключение составляет случай, когда один из товаров некачественный и не будет покупаться при любом доходе субъекта.

3. Кривые безразличия выпуклы вниз.

Наличие наборов товаров, обладающих одинаковой полезностью с точки зрения потребителя означает возможность замены одного набора другим равноценным набором.

Из условия (1.2.1) для двух товаров можно получить:

.

Откуда следует:

,

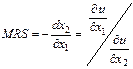т.е. предельная норма замены первого товара вторым равна отношению предельных полезностей первого и второго товаров. Предельная норма замены показывает, сколько требуется единиц второго товара, чтобы заменить единицу первого товара.