Глава 12. Неявная функция

§ 12.1. Теорема о существовании, непрерывности и дифференцируемости функции 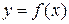, определяемой уравнением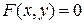

Термин «неявная функция» относится к способу задания функциональной зависимости между 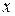и и 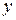означает, что вместо явной формулы 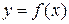эта зависимость представлена уравнением .

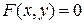Следует отметить, что уравнение 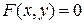не всегда определяет функцию 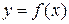. Например, уравнение 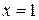функцию 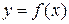не определяет. Кроме того, уравнение 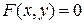не всегда позволяет однозначно выразить 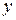через 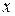. Например, уравнение 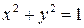, задающее окружность на плоскости, определяет при 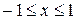две непрерывные функци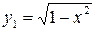и и .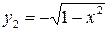

В этом примере можно, например, дополнительно потребовать чтобы выполнялось неравенство 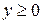. Тогда мы получим только .

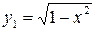В общей ситуации условия, при которых существует единственная функция 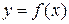, задаваемая уравнением 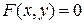, дает следующая теорема.

Теорема.12.1. Пусть 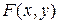определена и непрерывна вместе с частными производным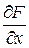и и 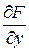в окрестности U точки такой, что 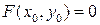и 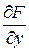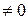. Тогда существуют числа и 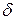такие, что на множестве 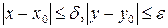уравнение 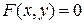равносильно уравнению 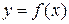где 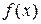непрерывная и дифференцируемая на 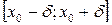функция, и .

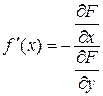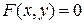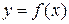Замечание.Равносильность и означает, что уравнение 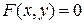однозначно определяет в рассматриваемой области дифференцируемую функцию 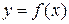такую, что 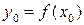, вообще, 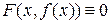при .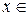

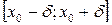► По условию 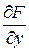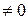. Пусть, для определенности,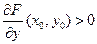

(если это не так, то просто меняем знак у левой части исходного уравнения).

 

По условию, производная непрерывна в окрестности и сохраняет знак,

следовательно, найдётся такая окрестность 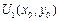всюду в пределах которой .

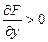Рассмотрим 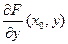, так как она положительна, 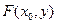возрастает для любых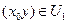

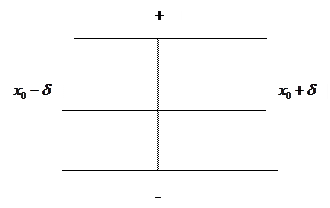
Фиксируем положительное число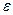

можно подобрать положительные и отрицательные окрестности и выбрать из них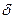

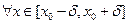Существует единственный 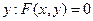. Каждому 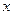сопоставим 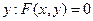. Назовем эту точку 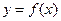. По построению мы получим непрерывную функцию 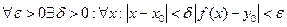Что равносильно тому, что как только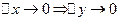

Рассмотрим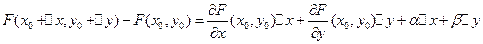

Получаем равенство

◄

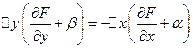
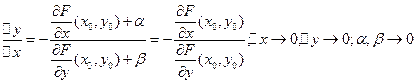ТеоремаПусть функция 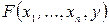непрерывна и имеет все непрерывные частные производные в окрестности точки 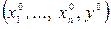такой, что 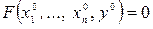, причем . Тогда существуют числа 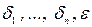такие, что в области 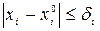, , 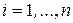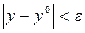уравнение 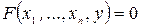равносильно уравнению 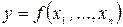, причем функция 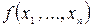непрерывна и имеет непрерывные частные производные, причем

.

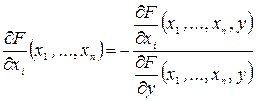2. Формулировка теоремы о существовании, непрерывности и дифференцируемости функции 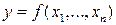определяемой уравнением 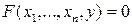. Формулировка теоремы о неявных функциях, определяемых системой уравнений

Теорема 19.2.Пусть функция 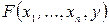непрерывна и имеет все непрерывные частные производные в окрестности точки 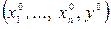такой, что 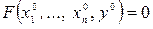, причем . Тогда существуют числа 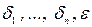такие, что в области 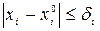, , 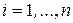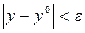уравнение 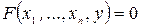равносильно уравнению 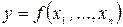, причем функция 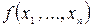непрерывна и имеет непрерывные частные производные, причем

.

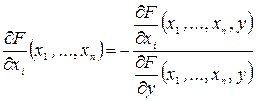►Доказывается так же, как и для случая ◄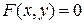

Рассмотрим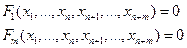

Параметрическое задание поверхности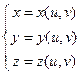

При каких условиях 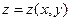и как найти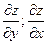

Дифференцируем и получаем

 

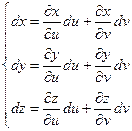
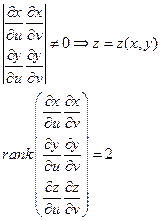
Ранг равен 2, следовательно, прямые не параллельны и образуют плоскость. Найдем нормаль к этой плоскости.

 

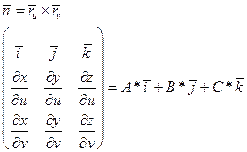
(уравнение касательной)

 

Либо такой вид билета.

ТеоремаПусть , (2.1)

где функции 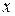, , 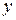непрерывны и имеют непрерывные производные в некоторой области (точки ). Пусть матрица Якоби имеет в этой области ранг 2. Тогда, если, например, минор , то в области систему можно преобразовать к уравнению

, , (2.2)

где есть непрерывно дифференцируемая функция от в области и

, , (2.3)

ЗамечаниеУравнения (2.1) определяют в некоторую поверхность и называются параметрическими уравнениямиэтой поверхности. Теорема утверждает, что поверхность есть график функции ((2.2)). Обозначают , и уравнения (2.1) принимают вид .

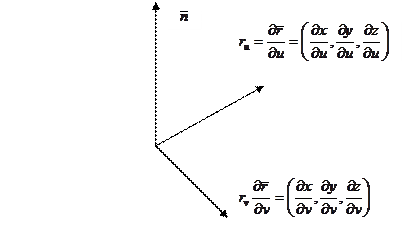
Если зафиксировать , то – уравнение координатной линии на (аналогично, при фиксированном также представляет собой уравнение координатной линии на ). Векторы и – касательные векторы к координатным линиям. Если взять точку поверхности, соответствующую параметрам и рассмотреть касательную плоскость в этой точке, то векторы и лежат в этой плоскости. Если ранг матрицы равен 2, это означает, что и не параллельны и их векторное произведение представляет собой нормальный вектор к касательной плоскости и

, (2.4)

где буквы , , обозначают соответствующие определители. В этих обозначениях формулы (2.3) принимают вид

, , (2.5)

а единичный вектор нормали (2.4), получаемый при делении вектора на его модуль , равен

 

(2.6)

Преобразуем выражение . По определению векторного произведения, , где – угол между и . Тогда

, (2.7)

где , , .

 

Понятие независимости функций. Рассмотрим систему функций

(1)

определенных и непрерывных, вместе со своими частными производными, в некоторой -мерной открытой области D.

Рассмотрим случай, когда значение одной из них, например , однозначно определяется совокупностью тех значений, которые принимают остальные функции

.

Точнее говоря, если есть множество таких -мерных точек, отвечающих всевозможным точкам в D, то предполагается что в будет иметь место функциональная зависимость

, (2)

причем это равенство оказывается тождеством относительно 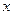в D, если вместо всех , подставить функции (1)­. Тогда говорят, что в области D функция зависит от остальных. Впрочем, для того, чтобы иметь возможность применять дифференциальное исчисление, мы включим в определение еще требование, чтобы функция была определена и непрерывна со своими частными производными в некоторой открытой области -мерного пространства, содержащей множество .

Если, в частности, одна из функций (1), , сводится к постоянной, то она явно будет зависеть от остальных: здесь можно просто положить . Функции называются вообще зависимыми в области D, если одна из них (все равно какая) зависит от остальных.

Примеры. 1) Если положить

то нетрудно проверить, что во всем -мерном пространстве будет выполняться тождество

.

2) Аналогично для функций

имеем тождественно (в трехмерном пространстве)

.

Все это – зависимые функции.

Если ни в области D, ни в какой-либо частичной, в ней содержащейся, области не имеет место тождество вида (18), то функции называют независимыми в области D.

Ответ на вопрос о независимости функций дает рассмотрение так называемой матрицы Якоби, составленной из частных производных этих функций по всем независимым переменным:

Предполагая , имеем такую теорему:

Теорема 1. Если хоть один определитель -ого порядка, составленный из элементов матрицы (3), отличен от нуля в области D, то в этой области функции независимы.

 

. (4)

Если бы не равным нулю был не этот, а какой-нибудь другой определитель, то, изменив нумерацию переменных, можно было бы свести вопрос к случаю (4).

Доказательство теоремы будем вести от противного. Предположим, что одна из функций, например , выражается через остальные, так что

, (5)

хотя бы в некоторой части D₀ области D.

Продифференцировав это тождество по каждой из переменных , мы получим ряд тождеств (в D₀) вида

.

Мы видим, что элементы последней строки определителя (5) получаются путем сложения соответственных элементов первых строк, умноженных предварительно на множители , , . Такой определитель, как известно, равен нулю. Это противоречит условию теоремы. Полученное противоречие доказывает невозможность равенства (5).