Пример решения задачи по теме.

 

Дана следующая трехфакторная функция порядковой полезности потребителя:

1. Доказать, что функция порядковой полезности является неоклассической.

2. Составить модель потребительского выбора и соответствующую ей задачу Лагранжа. Определить оптимальные по критерию максимума совокупной получаемой полезности объемы потребляемых благ. Для вектора рыночных цен на потребляемые блага и потребительского бюджета в размере определить численные значения требуемых показателей.

3. Проверить выполнение условия обратной зависимости предельной полезности денег от бюджета потребителя при потреблении им благ в оптимальных объемах.

4. Определить, являются ли рассматриваемые блага ценными или малоценными для потребителя, а также нормальными или особенными.

5. Определить коэффициент перекрестной эластичности спроса на первое благо при изменении цены на третье и дать экономическую интерпретацию полученного числа.

Решение:

1. Докажем, что рассматриваемая функция порядковой полезности является неоклассической, включая определение степени ее однородности. Определим первые и вторые частные производные ФПП:

Таким образом, рассматриваемая функция порядковой полезности определена и неотрицательна всюду на положительном ортанте , на котором существуют неотрицательные первые и неположительные вторые частные производные.

Рассматриваемая ФПП экономически непротиворечива:

(отсутствие полезности при нулевом потреблении благ).

Докажем, что ФПП является однородной:

Степень однородности r равна .

Исходя из вышеизложенного можно сделать вывод о том, что ФПП принадлежит классу неоклассических.

 

2. Составим модель рационального потребительского выбора и соответствующую ей задачу Лагранжа. Определим оптимальные по критерию максимума совокупной получаемой полезности объемы потребляемых благ.

Модель оптимального потребительского выбора имеет следующий вид:

Т. к. и функционал, и используемые ограничения являются непрерывными и дважды дифференцируемыми функциями на ортанте , то можно составить и провести анализ соответствующей этой задаче функции Лагранжа:

Необходимым условием экстремума функции является совместность следующей системы:

Определим необходимые частные производные:

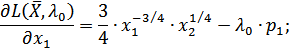
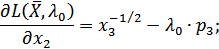
и построим систему уравнений, из которой найдем соотношения для объемов потребляемых благ 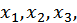а также для множителя Лагранжа :

Выразим соответственно из первого и второго уравнений системы (2.97), рассмотрим их отношение, из которого выразим :

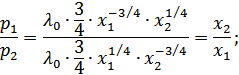
Выразим из второго уравнений системы (2.97), подставим полученный результат в третье уравнение системы (2.97), откуда выразим :

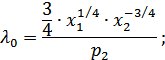
Подставим полученные результаты в четвертое уравнение системы (2.97):

Откуда:

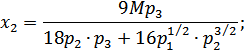
Из третьего уравнения системы (2.97) получим :

На основе полученных соотношений определим численные значения требуемых параметров:

 

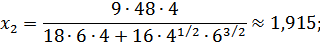
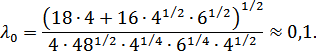
3. Проверим выполнение условия обратной зависимости предельной полезности денег от бюджета потребителя при потреблении им благ в оптимальных объемах.

Для этого определим частную производную функции 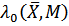предельной полезности денег, зависящей от объемов потребляемых благ и бюджета потребителя, по бюджету:

Знак «-» полученного выражения свидетельствует об обратной зависимости анализируемых показателей.

 

4. Определим, являются ли рассматриваемые блага ценными или малоценными для потребителя, а также нормальными или особенными.

Для того, чтобы определить, является ли - ое благо ценным для потребителя, необходимо найти знак коэффициента эластичности спроса на него по бюджету потребителя . Второй сомножитель выражения (2.24) всегда положителен; поэтому определим знак первого сомножителя, вычислив частную производную функции спроса на - ое благо по потребительскому бюджету индивида:

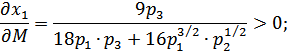
Знак «+» полученных выражений свидетельствует о прямой зависимости объемов потребляемых благ от бюджета потребителя, т.е. спрос на каждое благо растет при увеличении бюджета , и такие блага являются ценными для потребителя.

Для того, чтобы определить, является ли - ое благо нормальным, необходимо найти знак коэффициента эластичности спроса на - ое благо по цене на это же благо. Второй сомножитель выражения (2.28) всегда положителен; поэтому определим знак первого сомножителя, вычислив частную производную функции спроса на - ое благо по цене на это благо:

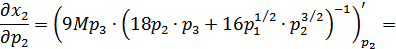
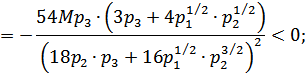
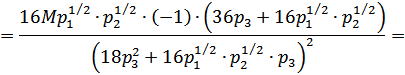
Знак «-» полученных выражений свидетельствует об обратной зависимости объемов потребляемых благ от их цены, т.е. спрос на все товары падает при увеличении их цены, и такие блага являются нормальными.

 

5. Определим коэффициент перекрестной эластичности спроса на первое благо при изменении цены на третье и дадим экономическую интерпретацию полученного числа.

Напомним, что реакцию рыночного спроса на - ое благо на перекрестное изменение цены на - ое отражает уравнение Слуцкого (2.46). В рамках поставленной задачи уравнение Слуцкого имеет вид:

где - множитель Лагранжа соответствующей задачи рационального потребительского выбора, 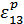- искомый коэффициент перекрестной эластичности спроса на первое благо при изменении цены на третье.

Получим аналитическое выражение для 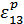из (2.98):

Определим численные значения необходимых частных производных:

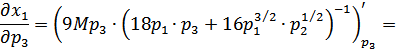
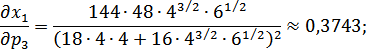
Определим численное значение требуемого коэффициента перекрестной эластичности спроса на первое благо при изменении цены на третье:

Т.е. при данных величине располагаемого дохода потребителя и уровнях рыночных цен на потребляемые блага для сохранения уровня получаемой полезности при увеличении (уменьшении) цены на третье благо на 1% индивиду следует увеличить (уменьшить) потребление первого блага приблизительно на 7,5%. Такие блага являются взаимозаменяющими.

 

[1] Покупка этого набора возможна в случае, если нет изначальной предпосылки необходимости потратить весь наличный бюджет.

[2] Функция может быть определена с точностью до линейного преобразования. Действительно, если - СФПП потребителя, то 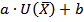(где a, b > 0) также СФПП.

[3] Т.к. рынок – категория первичная по отношению к покупателю, то соотношение (2.17) определяет закон формирования потребительского спроса по отношению к рыночным ценам, но не наоборот.

[4] Идея разложения общего эффекта изменения цены на эффект замены и эффект дохода впервые в экономической науке была представлена в статье российского экономиста и математика Е.Е. Слуцкого «К теории сбалансированного бюджета потребителя», опубликованной в итальянском «Giornale degli Economist» в 1915 г. Hо эта статья осталась для мировой науки незамеченной. Только благодаря работам Дж. Хикса и Р. Аллена, опубликованным значительно позже, научный мир был ознакомлен с этим результатом.

[5] С математическим доказательством обозначенных свойств читатель может ознакомиться, например, в параграфе 3.2 [O4].

[6] Эрнст Энгель (1821-1896 гг.) выяснил, что семьи с большим доходом тратят меньшую долю дохода на еду, что известно как закон Энгеля.

В терминах современной микроэкономики, это означает, что эластичность дохода по затратам на еду в этом случае меньше, чем аналогичный показатель, в случае, если еда является потребностью, а не роскошью. Зависимость между доходом и расходами на рассматриваемый предмет потребления стала известной как кривая Энгеля.

[7] По статистике примерно линейная зависимость между доходами и расходами на фрукты и ягоды. Трикотажные изделия, готовую одежду и рыбные продукты.

[8] Так, с ростом доходов затраты на продукты питания растут медленнее, чем затраты на одежду, обувь, жилье и т.п. На известном этапе наступает дальнейшая смена, когда рост затрат на одежду отстает от роста затрат, например, на предметы культурно-бытового назначения, и т.д.

[9] Как уже отмечалось выше, к основным факторам относятся активы потребителей, их личные качества (образование, способности и пр.), профессиональная принадлежность, национальность и др. Случайные (временные) компоненты – разного рода непредвиденные обстоятельства, меняющие шансы на получение дополнительного дохода.