Лабораторная работа 5

При создании использовалась монография «Тестирование учебных достижений» В.С. КИМ http://uss.dvfu.ru/static/kim_testing_monograph/index.html

Скопируем нашу матрицу с расчетами на новый лист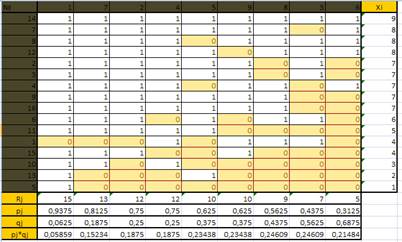

1. Вычислим доли верных p_i и долю неверных (q_i=1-p_i) ответов испытуемых.

Где Xi – индивидуальный балл испытуемого, М – количество заданий в тесте (количество столбиков после редуцирования). В нашем случае М = 9. Например, для испытуемого номер 7 (сохраняем нумерацию после упорядочивания матрицы) имеем p₇ = 8/9 =0,889. Создаем столбик (массив) «p_i» и считаем для каждого, протягиванием.

Считаем долю неверных ответов, от единицы отнимаем долю верных, создаем столбик «q_i» и рассчитываем для каждого испытуемого.

2. Вычисляем значения уровня подготовленности испытуемых по формуле

Для испытуемого номер 7 имеем: θ₇= ln(0,889/0,111)=2,07.Считаем для каждого испытуемого. Рядом теперь считаем квадрат значения уровня подготовленности θ².

Считаем сумму по столбику θ².

После этих расчетов имеем:

3. Вычисляем начальное значение трудности заданий по формуле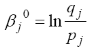

Значения q_j и p_j уже посчитаны ранее, используем их для подсчета. Считаем квадрат значения в новом массиве β².Считаем сумму по этому массиву.

После этих расчетов имеем:

4. Считаем среднее по столбцу «θ»и среднее по строчке «β».

5. Вычислить дисперсии

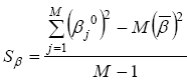
(N – количество испытуемых, М – количество заданий)

6. Вычислить угловые коэффициенты

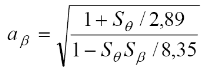
7. Запишем оценки параметров на единой интервальной шкале, сведем в таблицу (обозначим как «β» и «θ»)

8. Считаем стандартные ошибки измерения

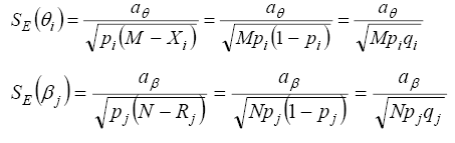
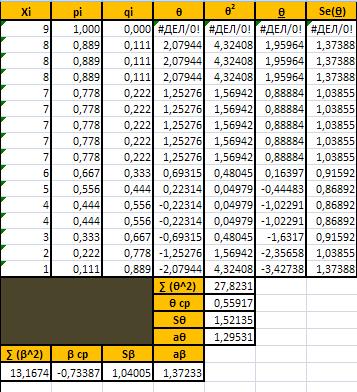
После расчетов имеем:

9. Строим график ICC (характеристические кривые заданий)

График ICC строится, например, по 15-20 точкам. Рассмотрим процесс определения первой точки для первого задания. Из таблицы видим, что первое задание имеет трудность β= -3,1571. Пусть переменная θ будет меняться в интервале от -5 до +5 с шагом 0,5 логита. Тогда у нас получится 21 точка. Точке №1 соответствует θ = -5. Вычислим значение вероятности успеха испытуемого с уровнем подготовленности -5 для задания с трудностью -3,1571. Сначала создаем таблицу (пишем -5 и ниже -4,5, протягиваем до 5), затем в вставляем формулу =(EXP(1,7*(C29-$B$22)))/(1+EXP(1,7*(C29-$B$22))), где С29 – ячейка со значение 5, а $B$22 замороженная ячейка со значением β= -3,1571. Протягиваем вниз и получаем набор точек, затем вставляем точечную диаграмму. Так же проделываем и для остальных значений β (всего у нас их 9). Просто вставляем формулу и меняем там букву в замороженной ячейке на следующую по алфавиту и протягиваем вниз. (То есть =(EXP(1,7*(C29-$С$22)))/(1+EXP(1,7*(C29-$С$22)), затем на месте С будет идти D и т.д. пока не дойдем до 9 задания).

10. Строим график PCC (характеристические кривые испытуемых)

Графики строятся аналогично, только теперь смотрим на значения θ. И уже значений будет не 9, а 16 (количество строчек). И менять мы будем не букву, а цифру, так как работаем со столбиком.

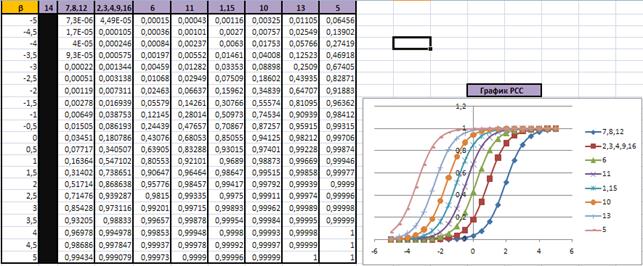Мы построили однопараметрическую модель Раша. Так как у нас были одинаковые значения, мы заносили их в один столбик, указывая номера через запятую.

11. Строим информационные функции, используя формулу

У нас она примет вид: =2,89*((EXP(1,7*(T2-$P$3)))/((1+EXP(1,7*(T2-$P$3)))^2))

Проделываем все аналогично предыдущему пункту (создаем столбик с шагом 0,5 начиная с -5, до 5, протягиваем формулу, предварительно меняя значение). Можно построить для каждого задания.

12. Чтобы построить общую функцию для всего теста, необходимо найти суммы по строчкам.

(Всего 21 сумма, так как 21 строчка от -5 до 5)

После расчетов и построения имеем: сначала идут графики информационных функций каждых заданий, а затем ниже, уже общая информационная функция.