Порядок выполнения работы
1.3.1.Для каждого распределения п. 1.2.8 вывести в одно графическое окно два графика плотности вероятности. Один из графиков плотности вероятности получить по собственной программе, написанной для расчета значений функции плотности вероятности по формулам п. 1.2.8, второй – с использованием функций системы Matlab. Исследовать их зависимость от параметров распределений.
1.3.2.Для каждого распределения п. 1.2.8 вывести в отдельное графическое окно график функции распределения с использованием функций системы Matlab.
Исследовать их зависимость от параметров распределений.
Отчет:
1. Равномерное распределение U(a,b):
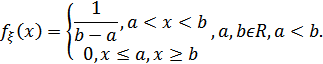
>>x=0:0.5:7;
>>b=4;
>>a=2;
>>chisl=1;
>>znam=b-a;
>>drob=chisl/znam;
>>plot(x,a)

Рисунок 1 График плотности вероятности равномерного распределения
2. Нормальное (гауссовское) распределение.
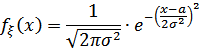



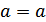
f = sm1 * sm2;
sm1 = 1/sqrt(2*3,14*sig.^2);
sm2 = exp(-drob);
drob = chisl/znam;
chisl = (x – a).^2;
znam = 2*sig.^2;
x = 0: 0.01 : 10;
a = 5;
sig = 2;
znam = 2*sig.^2;
chisl = (x – a).^2;
drob = chisl/znam;
sm2 = exp(-drob);
sm1 = 1/sqrt(2*3,14*sig.^2);
f = sm1 * sm2;
plot(x,a);
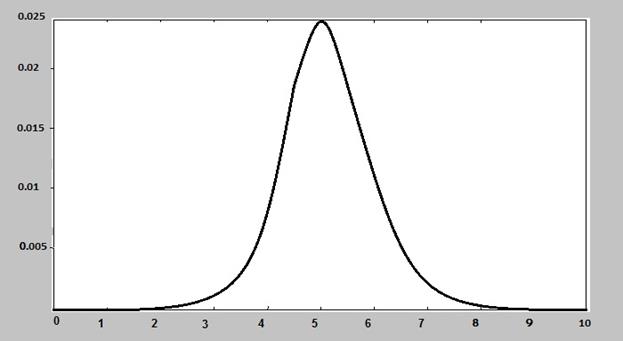
Рисунок 2 – График плотности вероятности нормального (гауссовского) распределения
3. Экспоненциальное распределение:

lambda=1,2;
x=0:0.1:8;
y1=lambda.^-1;
>>y2=y1*x;
>>y3=exp(y2);
>>y=y1*y3;
>>plot(x,y)

Рисунок 3 – График плотности вероятности экспоненциального распределения
Вывод:
1. Мы ознакомились с работой программы MatLab и попробовали рассчитать в ней уравнения.
2. Мы ознакомились с языком программирования MatLab.
3. Мы исследовали с помощью средств MatLab одномерных распределений теории вероятностей и математической статистики и получили график распределения.