Пример.
>> digits(30); vpa(pi)
ans = 3.14159265358979323846264338328
В примере получили прекрасный результат - число  с 30 значащими знаками, при чём ответ ans оказался принадлежащим новому классу – sym object. Другими словами Symbolic Math Тооlbох работает с данными нового типа – с символьными объектами.
с 30 значащими знаками, при чём ответ ans оказался принадлежащим новому классу – sym object. Другими словами Symbolic Math Тооlbох работает с данными нового типа – с символьными объектами.
y1=y; s2=['n=' num2str(n)]; hText=text(1.5, 1.5^2*n-1, s2); set(hText,'FontSize',[14]); end
Пример. Построить семейство функций 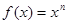 (
( 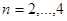 ) и найти их общие точки, причём в объекте Figure подписать графики и точки, обозначить оси, подписать заголовок
) и найти их общие точки, причём в объекте Figure подписать графики и точки, обозначить оси, подписать заголовок 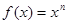 и использовать разные цвета для построенных графиков. При решении использовать функцию num2str(x), переводящее число x в строковую величину:
и использовать разные цвета для построенных графиков. При решении использовать функцию num2str(x), переводящее число x в строковую величину:
>> x=-2:0.1:2;
title('{\itf(x)=x^{n}}');
xlabel('x');
ylabel('y');
hFigure=gcf;
set(hFigure,'Color',[1 1 1]);
hText=text;
set(hText,'FontSize',[18]);
for n=2:4
y=x.^n;
hold on
hPlot=plot(x,y);
set(hPlot,'Color',[1.8/n 0.7 0.5]);
set(hPlot,'LineWidth',2);
if n~=2
for i=1:length(y)
s='';
if y(i)==y1(i)
hold on
plot(x(i),y(i),'ko');
s=['(' num2str(x(i)) ',' num2str(y(i)) ')'];
hText=text(x(i),y(i)+2, s); set(hText,'FontSize',[16]);
end
end
end
y1=y; s2=['n=' num2str(n)];
hText=text(1.5, 1.5^2*n-1, s2); set(hText,'FontSize',[14]);
end
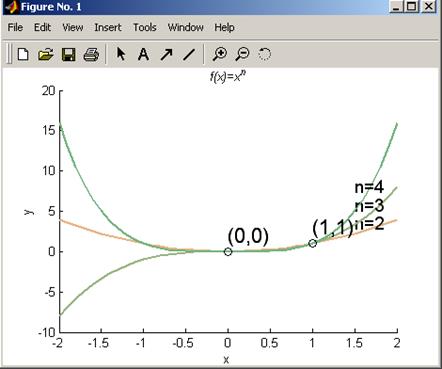
Рис. 12