Первое уравнение системы (2.5.3) можно преобразовать к виду

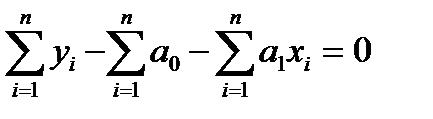
или

.

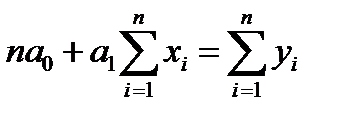Второе уравнение можно преобразовать к виду

.

Таким образом, мы имеем систему уравнений

 

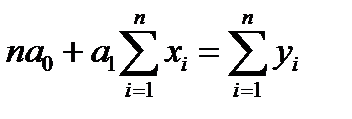; (2.5.4)

,

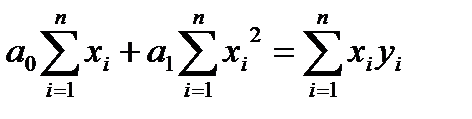Разделив обе части уравнений (2.5.4) на n, получим систему уравнений в виде

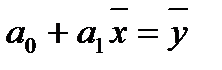(2.5.5)

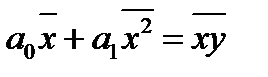
где соответствующие средние определяются по формулам

; ;

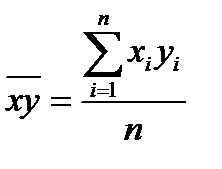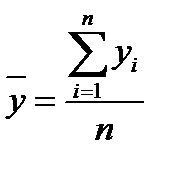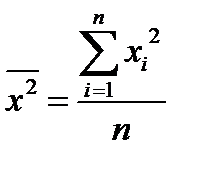; . (2.5.6)

Подставляя значение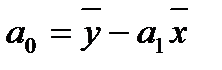

из первого уравнения системы (2.5.5) во второе, получим

 

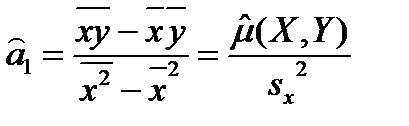, (2.5.7)

где - выборочная дисперсия переменной Х:

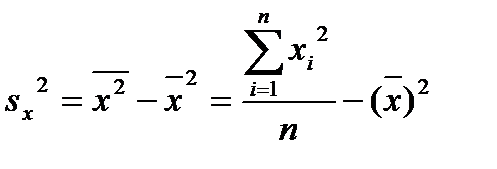, (2.5.8)

- выборочная ковариация:

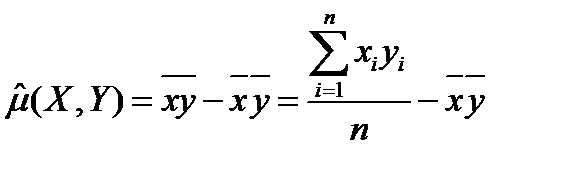. (2.5.9)

Отметим, что линия регрессии проходит через точку 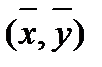, то есть

.

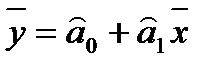В заключение приведем удобные для расчета оценок параметров формулы:

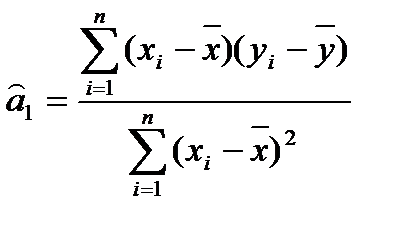, (2.5.10)

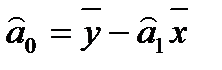. (2.5.11)

Если рассчитан выборочный коэффициент корреляции 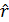, то коэффициенты a₀ и a₁ могут быть определены следующим образом

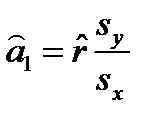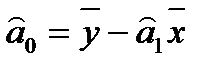, , (2.5.12)

где 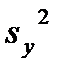- выборочная дисперсия переменной Y:

 

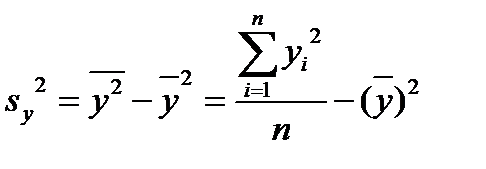
В качестве оценки дисперсии случайной компоненты 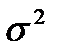используется

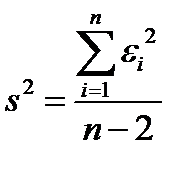. (2.5.13)

При выполнении предположений 1-4 доказано, что оценки параметров 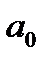и 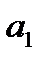по методу наименьших квадратов и 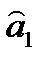являются несмещенными с минимальными дисперсиями в классе линейных оценок (т. е. эффективными).

Кроме того, статистика 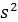является несмещенной оценкой дисперсии .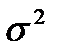