РЕШЕНИЕ ТИПОВОГО ПРИМЕРА

 

Пусть исходные данные представлены таблицей 4.

Таблица 4 – Исходные данные

X1	23,2	37,2	35,1	20,0	37,9	20,1	23,4	13,4
X2
X3	0,63	1,18	1,12	0,44	1,19	0,48	0,65	0,26

 

1. Находим значения выборочных средних и выборочных средних квадратических отклонений S₁, S₂, S₃ по следующим формулам:

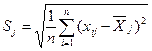, j = 1, 2, 3.

Получаем:

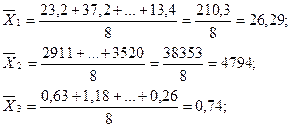
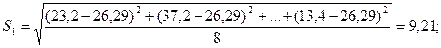
Находим матрицу R выборочных коэффициентов корреляции между переменными. Элементы матрицы R -выборочные коэффициенты корреляции - вычисляются по формуле:

, i, j = 1, 2, 3.

Имеем, например,

Аналогично вычисляем остальные коэффициенты корреляции, в результате чего окончательно получаем матрицу:

.

Матрица R парных коэффициентов корреляции характеризует тесноту линейной связи между признаками X₁, X₂ , X₃. В данном примере можно сделать предварительный вывод о тесной линейной связи между всеми этими признаками.

 

2. Более тонкий анализ связей проводится на основе вычисления частных коэффициентов корреляции, которые выясняют тесноту линейной связи между двумя показателями при исключении влияния третьего. Важность такого анализа объясняется возможностью ситуации, когда, например, признаки X₁, X₂ не имеют тесной линейной связи, а высокое значение парного коэффициента корреляции между ними обусловлено тем, что оба они находятся в тесной связи с третьим признаком X₃. Отсекая всякий раз влияние одного из признаков X₁, X₂ , X₃, частные коэффициенты корреляции r_23.1, r_13.2, r_12,3 дают точную картину взаимного влияния показателей X₁, X₂ , X₃ друг на друга.

Частные коэффициенты корреляции вычисляются по формуле:

,

где R_ij - алгебраическое дополнение элемента r_ij матрицы R.

Напомним, что алгебраическим дополнением R_ij элемента r_ij матрицы R называется произведение (–1)^i+j на определитель второго порядка, получаемый из матрицы R вычеркиванием строки и столбца 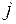, на пересечении которых этот элемент стоит.

Рассчитаем для типового примера матрицу, состоящую из алгебраических дополнений элементов матрицы. Заметим при том, что матрица R – симметричная (r_ij = r_ji), то симметричной будет и матрица алгебраических дополнений ее элементов.

Получаем:

R₁₁ = 1*1 – 0,876*0,876 = 0,234;

R₂₂ = 1*1 – 0,997*0,997 = 0,006;

R₃₃ = 1*1 – 0,87*0,87 = 0,243;

R₁₂ = R₂₁ = –(1*0,87 – 0,997*0,875) = 0,00337;

R₁₃ = R₃₁ = 0,876*0,87 – 0,997*1 = –0,236;

R₂₃ = R₃₂ = –(1*0,876 – 0,997*0,87) = –0,0086.

Рассчитаем частные коэффициенты корреляции:

;

;

.

 

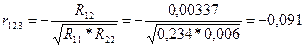3. Множественный коэффициент корреляции результативного показателя с остальными факторами определяется по формуле:

,

где |R| = R₁₁ + r₁₂R₁₂ + r₁₃R₁₃.

Подсчитаем множественный коэффициент корреляции для типового примера:

|R| = 0,234+0,87*0,00337+0,997*(-0,236) =0,00164,

следовательно,

 

4. Определим значимость парных коэффициентов корреляции r₁₂, r₁₃, r₂₃, частных коэффициентов корреляции r_12.3, r_13.2, r_23.1 и множественного коэффициента корреляции R_1.23.

Для определения значимости парных и частных коэффициентов корреляции используется критерий Стьюдента, наблюдаемое значение которого вычисляется по формуле:

,

где r – расчетное значение парного или частного коэффициента корреляции, k = 0 для парных коэффициентов корреляции и k = 1 для частных коэффициентов корреляции.

Для выбранного уровня значимости α = 0,05 и числа степеней свободы v = n – k – 2 по таблицам распределения Стьюдента ищется критическое значение критерия t_крит(α,v). Коэффициент корреляции является значимым, если t_набл > t_крит(α,v). Если же t_набл ≤ t_крит(α,v), то считают, что нет оснований отвергнуть нулевую гипотезу о незначимости коэффициента корреляции.

В нашем случае для парных коэффициентов корреляции получаем:

t_крит(α,v) = t_крит(0,95; 8 – 0 – 2) = t_крит(0,95; 6) = 2,447,

а для частных коэффициентов корреляции:

t_крит(α,v) = t_крит(0,95; 8 – 1 – 2) = t_крит(0,95; 5) = 2,571.

Вычисляем значения t_набл:

значим;

значим;

значим;

не значим;

значим;

не значим.

Для множественного коэффициента корреляции R_1.23 проверка гипотезы о значимости основана на использовании критерия Фишера F. Наблюдаемое значение критерия находят по формуле:

.

Далее выбирают уровень значимости α = 0,05, степени свободы v₁ = 2, v₂ = n – 2, находят по таблицам Фишера критическое значение F_крит(α,v₁,v₂) и сравнивают с F_набл. Если F_набл > F_крит(α,v₁,v₂), то множественный коэффициент корреляции r_1.23 является значимым, в противном случае значимость коэффициента корреляции считается не доказанной. Для типового примера имеем:

;

F_крит(α,v₁,v₂) = F_крит(0,05; 2; 6) = 5,14.

Так как F_набл > F_крит(α,v₁,v₂), то множественный коэффициент корреляции R_1.23 является значимым.