Уравнения регрессии

В статистической практике точечные оценки параметров всегда дополняют их интервальными аналогами. Для полученных выше оценок b₁ и b₀ укажем границы интервалов, которые с заданной вероятностью накрывают истинные значения b₁ и b₀.

Любое значение b₁, совместимое с оценкой b₁, удовлетворяет условию:

, или .

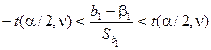Разрешив это неравенство относительно b₁, получим для него доверительный интервал:

(13)

Доверительный интервал (13) накрывает истинное значение параметра b₁ с заданной доверительной вероятностью g = (1 – a).

Аналогично получаем доверительный интервал для b₀:

(14)

В отношении (13), (14) справедливы общие правила: чем уже доверительный интервал, тем точнее оценка параметра; если доверительный интервал включает нулевое значение, то оцениваемый параметр статистически незначим (равен нулю).