Предпосылки метода наименьших квадратов (условия Гаусса-Маркова)

1. Математическое ожидание случайного отклонения равно нулю для всех наблюдений. Данное условие означает, что случайное отклонение в среднем не оказывает влияния на зависимую переменную. В каждом конкретном наблюдении случайный член может быть либо положительным, либо отрицательным, но он не должен иметь систематического смещения.

2. Дисперсия случайных отклонений постоянна для любых наблюдений. Это условие подразумевает, что несмотря на то, что при каждом конкретном наблюдении случайное отклонение может быть либо большим, либо меньшим, не должно быть некой априорной причины, вызывающей большую ошибку (отклонение).

3. Случайные отклонения u_i и u_j являются независимыми друг от друга для i¹j. Выполнимость данной предпосылки предполагает, что отсутствует систематическая связь между любыми случайными отклонениями. если данное условие выполняется, то говорят об отсутствии автокорреляции.

4. Случайное отклонение должно быть независимо от объясняющих переменных.

Обычно это условие выполняется автоматически, если объясняющие переменные не являются случайными в данной модели. Данное условие предполагает выполнимость следующего соотношения:

5. Модель является линейной относительно параметров.

Теорема Гаусса-Маркова. Если предпосылки 1-5 выполнены, то оценки, полученные по МНК, обладают следующими свойствами:

1. Оценки являются несмещенными,

2. Оценки состоятельны,

3. Оценки эффективны, то есть они имеют наименьшую дисперсию по сравнению с любыми оценками данных параметров, линейными относительно величин y_i.

 

39. Каковы последствия мультиколлинеарности факторов?

Мультиколлинеарностью называется линейная взаимосвязь двух или нескольких объясняющих переменных, которая может проявляться в функциональной (явной) или стохастической (скрытой) форме.

Если факторные переменные связаны строгой функциональной зависимостью, то говорят о полной мультиколлинеарности. Вид мультиколлинеарности, при котором факторные переменные связаны некоторой стохастической зависимостью, называется частичной. Частичная мультиколлинеарность приводит к следующим последствиям:
· увеличение дисперсий оценок параметров расширяет интервальные оценки и ухудшает их точность;
· уменьшение t-статистик коэффициентов приводит к неверным выводам о значимости факторов;
· неустойчивость МНК-оценок и их дисперсий.
Точных количественных критериев для обнаружения частичной мультиколлинеарности не существует. О наличии мультиколлинеарности может свидетельствовать близость к нулю определителя матрицы (X^TX). Также исследуют значения парных коэффициентов корреляции.

 

40. В чем суть взвешенного МНК?

Метод наименьших квадратов (МНК, англ. Ordinary Least Squares, OLS) — математический метод, применяемый для решения различных задач, основанный на минимизации суммы квадратов некоторых функций от искомых переменных. Он может использоваться для «решения» переопределенных систем уравнений (когда количество уравнений превышает количество неизвестных), для поиска решения в случае обычных (не переопределенных) нелинейных систем уравнений, для аппроксимации точечных значений некоторой функцией. МНК является одним из базовых методов регрессионного анализа для оценки неизвестных параметров регрессионных моделей по выборочным данным.

Суть МНК: задача заключается в нахождении коэффициентов линейной зависимости, при которых функция двух переменный a и b принимает наименьшее значение. То есть при данных a и b сумма квадратов отклонений экспериментальных данных от найденной прямой будет наименьшей. Таким образом, решение примера сводится к нахождению экстремума функции двух переменных.

 

41. Каковы последствия автокорреляции и гетероскедастичности ошибок

Автокорреляцией остатков модели регрессииei (или случайных ошибок регрессии модели ?i) называется корреляционная зависимость между настоящими и прошлыми значениями остатков.

Последствия, к которым может привести наличие в модели регрессии автокорреляции остатков, совпадают с последствиями, к которым может привести наличие в модели регрессии гетероскедастичности:

1) оценки неизвестных коэффициентов нормальной линейной модели регрессии являются несмещёнными и состоятельными, но при этом теряется свойство эффективности;

2) существует большая вероятность того, что оценки стандартных ошибок коэффициентов модели регрессии будут рассчитаны неверно, что конечном итоге может привести к утверждению неверной гипотезы о значимости коэффициентов регрессии и значимости модели регрессии в целом.

Наиболее наглядным способом обнаружения автокорреляции случайных остатков регрессионной модели является графический метод. При этом осуществляется построение графиков автокорреляционной и частной автокорреляционной функций.

 

42. В чем суть обобщенного МНК?

Обобщённый метод наименьших квадратов (ОМНК, GLS — англ. Generalized Least Squares) — метод оценки параметров регрессионных моделей, являющийся обобщением классического метода наименьших квадратов. Обобщённый метод наименьших квадратов сводится к минимизации «обобщённой суммы квадратов» остатков регрессии — , где — вектор остатков, — симметрическая положительно определенная весовая матрица. Обычный МНК является частным случаем обобщённого, когда весовая матрица пропорциональна единичной. Необходимо отметить, что обычно обобщённым методом наименьших квадратов называют частный случай, когда в качестве весовой матрицы используется матрица, обратная ковариационной матрице случайных ошибок модели.

Формула обобщённого МНК имеет вид:

Ковариационная матрица этих оценок равна:

 

43. Какие проблемы возникают при построении моделей с лаговыми переменными?

Отличительной особенностью моделей данного типа является наличие в них лагированных переменных, т. е. переменных, взятых в предыдущие моменты времени.

Часто при моделировании экономических процессов на зависимую переменную влияют не только текущие значения объясняющего фактора, но и его лаги.

Модели данного типа встречаются тогда, когда эндогенная переменная с запаздыванием реагирует на изменения экзогенной переменной. При этом в модель могут входить лагированные значения экзогенной переменной (модель распределенных лагов), например, или эндогенной переменной (авторегрессионная модель): либо одновременно и те и другие (авторегрессионная модель распределенных лагов).

Появление лаговых значений зависимой переменной в правой части эконометрической модели часто значительно осложняет проблему получения несмещенных и эффективных оценок ее параметров. Это может произойти из-за воздействия целого ряда обстоятельств.

Во-первых, наличие нескольких лаговых переменных y_t–1, y_t–2,... зачастую имеет своим следствием плохо обусловленную матрицу X¢X по причине достаточно сильной автокорреляционной зависимости между соответствующими ее столбцами. Этот факт, как и в моделях с лаговыми независимыми переменными, ведет к потере качества модели вследствие ухудшения точности оценок ее параметров, снижению их эффективности и устойчивости к незначительным колебаниям исходной информации, ошибкам округления.

Во-вторых, для подобного рода моделей характерной чертой является существование сильной корреляционной зависимости между переменными y_t–1, y_t–2, ... и ошибкой e_t, что, в свою очередь, ведет к появлению смещения в оценках их параметров при использовании МНК.

В-третьих, временной ряд ошибки модели e_t часто характеризуется наличием автокорреляционной связи, вследствие чего оценки параметров модели, полученные непосредственно на основе МНК являются неэффективными.

 

44. Каковы причины нелинеаризуемости моделей?

Нелинейная модель, а точнее нелинеаризуемая форма основного уравнения эконометрической модели, создает существенные трудности при оценке значений ее параметров. Кроме того, некоторые проблемы в этом случае возникают и при определении характеристик качества построенных вариантов модели, включая и показатели точности найденных значений их параметров. В основном появление этих (и некоторых других) проблем обусловлено невозможностью получения решения задачи оценивания параметров в аналитическом виде, как это имело место а случае линейных эконометрических моделей.

Поясним происхождение этих проблем на примере двухфакторной нелинейной модели следующего вида:

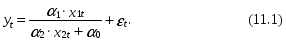
Попытаемся использовать при определении оценок a₀, a₁, a₂ ее параметров a₀, a₁, a₂ метод наименьших квадратов при условии, что значения переменныху_t, х_1t и х_2t, t=1, 2,..., Т известны. Сумма квадратов ненаблюдаемых значений ошибки е_t, t=1, 2,..., Т; в данном случае может быть представлена в следующем виде:

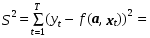
В соответствии с выбранным критерием искомые значения оценок a₀, a₁, a₂ должны удовлетворять условию минимума функции S², что приводит к появлению трех уравнений: Учитывая, что S² определено выражением (11.2), представим эти уравнения в виде следующей системы (аналога системы нормальных уравнений):

Несложно заметить, что уравнения системы (11.3) являются нелинейными относительно неизвестных значений a₀, a₁ и a₂. При этом нелинейность в данном случае усугубляется необходимостью суммирования сложных функций, выраженных отношениями и квадратами зависимой и независимой переменных модели. Решение системы (11.3) можно получить, только используя достаточно сложные итеративные процедуры нахождения ее корней. При этом следует заметить, что для другой формы эконометрической зависимости, отличной от выражения (11.1) будет получена и другая, отличная от вида (11.3) система нелинейных уравнений. Для ее решения возможно придется применять и другую процедуру, учитывающую специфические особенности формы ее уравнений.

 

 

45. В чем состоит суть методов Гаусса?

Пусть дана система
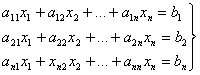, ∆≠0. (1)

 

Метод Гаусса – это метод последовательного исключения неизвестных

 

Суть метода Гаусса состоит в преобразовании (1) к системе с треугольной матрицей, из которой затем последовательно (обратным ходом) получаются значения всех неизвестных.