Алгоритм поиска незначащих переменных в парной регрессионной модели.

В качестве меры влияния регрессора на формирование значения эндогенной переменной вводится коэффициент детерминации как отношение регрессионной суммы квадратов к общей

R²⁼ (1)

R²ϵ

R²=0: RSS = 0; ESS = TSS

R²=1: RSS = TSS; ESS = 0

Коэффициент детерминации имеет смысл только при наличии свободного коэффициента спецификации.
В случае парной линейной регрессии коэффициент детерминации равен квадрату коэффициента корреляции между переменными y и x.

 

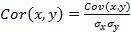
R² = Cor²(x,y)

Коэффициент Детерминации – величина случайная, так как его значение вычислено по случайной выборке. Следовательно, для тестирования гипотезы о том,что выбранный регрессор не оказывает вляиния на формирование значения эндогенной переменной, согласно алгоритму проверки статистической гипотезы, необходимо создать случайную переменную, закон распределения которой известен.

Если известен R², то в качестве такой переменной принимается Fтест

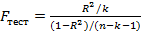(2)

n-объем выборки

k – количество регрессоров

F_тест подчиняется закону распределения Фишера с параметрами k и (n-k-1).

Приняв значение доверительной вероятности, вычисляется критическое значение переменной.

Если F_тест ≤ F_крит (3), то принимается гипотеза о том, что регрессор x не влияет на формирование значения y.

Если условие (3) не выполняется, то принимается альтернативная гипотеза о том,что регрессор существенно влияет на формирование переменной y.