Пример 4.

Пусть 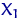, , – выборка объема из распределения Пуассона , где 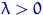. Найдем оценку максимального правдоподобия неизвестного параметра .

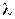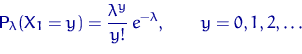
Поскольку эта функция при всех 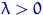непрерывно дифференцируема по 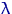, можно искать точки экстремума, приравняв к нулю частную производную по 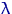. Но удобнее это делать для логарифмической функции правдоподобия:

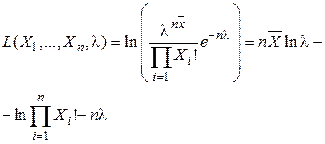
Тогда

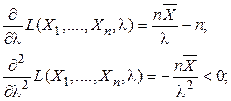
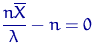и точка – решение уравнения: , ,-точка максимума ф-ции правдоподобия.