Этап 4. Моделирование временного ряда применяя методологию Бокса-Дженкинса.

Анализ динамических рядов часто показывает, что значение показателя в рассматриваемый момент времени находится в некоторой зависимости от значений в предшествующий период. Это явление носит название автокорреляции. Для обнаружения такого эффекта могут быть предложены различные методы.

Предварительный анализ АКФ, ЧАКФ:

Рисунок 10. Автокорреляционная функция индекса РТС.

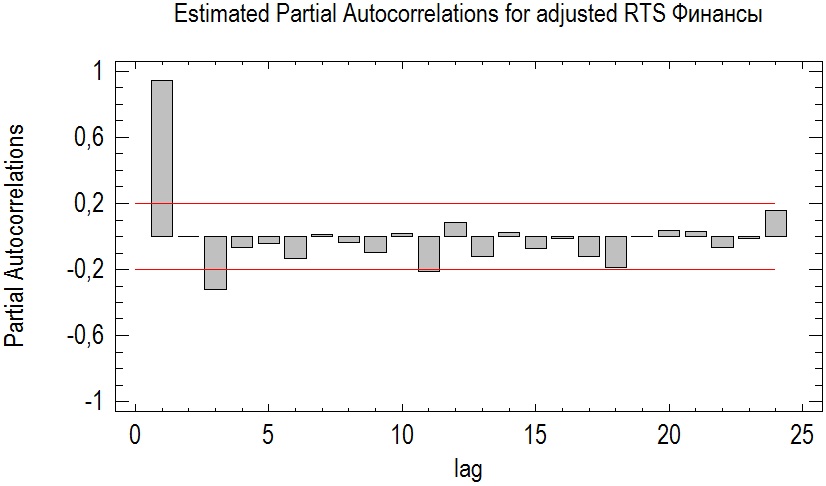
Рисунок 11. Частная автокорреляционная функция индекса РТС.

Описательная статистика временного ряда говорит о наличии автокорреляции 6-ого порядка. Частная автокорреляционная функция имеет 3 значимых показателя в первом, третьем и двенадцатом лагах.

Проверим временной ряд на стационарность при помощи расширенного теста Дикки-Фуллера. Расширенный критерий Дикки-Фуллера предполагает оценить параметры модели:

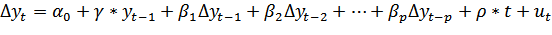
при помощи критических значений статистик Дикки-Фуллера,

где 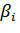– коэффициенты при дополнительных лаговых переменных;

– номер включенного дополнительного лага;

– остатки без автокорреляции, т.е. «белый шум».

В нашем случае, мы проверяем значимость только параметра 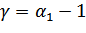. Данная проверка носит название теста на наличие единичных корней (unit-root test). Нулевая гипотеза: , т.е. ряду соответствует единичный корень (временной ряд нестационарен). Альтернативная гипотеза: | | < 1 – временной ряд стационарен.

Для проведения теста на наличие единичных корней воспользуемся возможностями пакета Eviews:

Null Hypothesis: RTS has a unit root
Exogenous: Constant
Lag Length: 2 (Automatic - based on AIC, maxlag=11)


			t-Statistic	Prob.*


Augmented Dickey-Fuller test statistic	-2.107959	0.2421
Test critical values:	1% level		-3.503879
	5% level		-2.893589
	10% level		-2.583931


*MacKinnon (1996) one-sided p-values.


Augmented Dickey-Fuller Test Equation
Dependent Variable: D(RTS)
Method: Least Squares
Date: 11/14/12 Time: 23:55
Sample (adjusted): 2005M04 2012M10
Included observations: 91 after adjustments


Variable	Coefficient	Std. Error	t-Statistic	Prob.


RTS(-1)	-0.054956	0.026071	-2.107959	0.0379
D(RTS(-1))	0.193071	0.102805	1.878034	0.0637
D(RTS(-2))	0.222954	0.103449	2.155199	0.0339
C	22.72194	11.49079	1.977405	0.0512


R-squared	0.130041	Mean dependent var	1.580769
Adjusted R-squared	0.100042	S.D. dependent var	50.42421
S.E. of regression	47.83548	Akaike info criterion	10.61637
Sum squared resid	199076.3	Schwarz criterion	10.72674
Log likelihood	-479.0450	Hannan-Quinn criter.	10.66090
F-statistic	4.334903	Durbin-Watson stat	2.042743
Prob(F-statistic)	0.006765

Таблица №11. Расширенный тест Дикки-Фуллера.

return false">ссылка скрыта

Полученный уровень значимости (Prob. = 0,0068) свидетельствует, что нулевая гипотеза о наличии единичного корня не отвергается, а, следовательно, исходный ряд стационарен относительно стохастического тренда. Также можно рассуждать следующим образом: процесс y_t стационарен, т.к. параметр 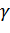получился отрицательным и по модулю меньше единицы. Таким образом, временной ряд относится к классу TSP (с детерминированным трендом).

Таким образом, параметр d можно ставить равным 0.

Приведем сравнения моделей ARIMA с разными параметрами, так чтобы уменьшить среднеквадратическую ошибку RMSE:

(A) ARIMA(6,0,3)

(B) ARIMA(1,0,0)

(D) ARIMA(2,1,0)

(E) ARIMA(2,0,1)