Определение опасности фрагментов кода

 

В настоящее время за счет существенного расширения номенклатуры и возможностей средств информационного воздействия эффективность средств защиты информации заметно снизилась, особенно при конфликтном взаимодействии с информационными системами при их априорно неизвестном назначении. При этом значительная неопределенность взаимодействия (вплоть до его конкретного характера – конфликт или кооперация) в наибольшей степени проявляется на нижних уровнях информационно-коммуникационного комплекса, так как элементы этих уровней в процессе реализации своих целевых функций решают лишь узкоспециальные частные задачи, в частности обнаружения средств информационного воздействия по известной сигнатуре. Отсутствие в этих элементах описания целей системы в целом, целей элементов взаимодействующей системы (например, информационного воздействия) приводит к заметному снижению эффективности реализации целевых функций, особенно, в условиях интенсивного информационного конфликта.

Тем не менее, современные концепции синтеза оптимального управления информационно-коммуникационных комплексов (ИКК) как основу реализации их целевой функции рассматривают классификацию текущей ситуации (текущего состояния объекта управления) с целью сведения его к некоторой априорно заданной обобщенной ситуации. Применительно к случаю взаимодействия ИКК такая классификация эквивалентна решению задачи определения режима взаимодействия, то есть отнесения его к классу конфликтных или бесконфликтных (нейтральному или кооперативному). Существенной особенностью такой классификации является необходимость ее проведения в условиях значительной неопределенности параметров анализируемого потока унитарных кодов и их сопоставления с заданным уровнем опасности при ограничении информационно-временного ресурса как средства идентификации, так и средства защиты информации.

В соответствии с известным определением информационного воздействия как фрагмента потенциально опасного кода, обнаружение и идентификация такого фрагмента в последовательности унитарных кодов, поступающих на вход элементов ИКК, может быть осуществлено на основе анализа изменения вероятности реализации целевой функции этим комплексом при взаимодействии с этим потенциально опасным фрагментом. Если такое взаимодействие носит конфликтный характер, вероятность реализации целевой функции ИКК будет заметно снижена, что в ряде случаев может привести к невозможности дальнейшего решения комплексом своей центральной задачи, несмотря на успешное обнаружение указанного фрагмента.

Предлагаемый в данном пособии подход к решению задачи идентификации текущего состояния и оценки опасности конкретного пакета унитарного кода основывается на разделении анализируемых последовательностей на два класса − потенциально опасных, содержащих обращения к запрещенным областям вычислительного процесса, где выполнение этих последовательностей может привести к снижению вероятности реализации целевой функции до уровня ниже заданного, и безопасных, располагающихся в заданной информационной области ИКК. При этом понятия запрещенной и разрешенной области пространства унитарных кодов ИКК относительны, так как отдельные обращения к этим областям не являются критерием конфликтности или бесконфликтности соответствующего компонента, фрагмента кода. Примером такого разделения может служить хорошо известное разграничение области функционирования процессора на кольца защиты. При этом в качестве критерия конфликтности может использоваться значение некоторого функционала, основанного на свертке поступившего кода и функции критических точек входа, а также статистике обращений к этим точкам. При этом, как показывает анализ обращений к критическим точкам входа, статистики обращения (в том числе запросы на исполнение) к унитарным кодам рассмотренных классов существенно различаются для конфликтного и бесконфликтного взаимодействия, а сравнение некоторых специальных функционалов рассматриваемых статистик может быть использовано для идентификации режима взаимодействия.

Основная идея такого подхода заключается в представлении динамики функционирования ИКК в виде движения рабочей точки по некоторой дискриминационной поверхности, форма которой определяется свойствами системы. При этом вся совокупность вычислительных процессов, определяемая движением рабочих точек для каждого процесса обработки получаемой ИКК последовательности унитарных кодов (вычислительного процесса), может быть представлена некоторой апериодической, хаотической траекторией (или орбитой процесса) конфликтного функционирования, сформированной в области периодических неустойчивых траекторий бесконфликтного режима. Каждая совокупность траекторий, выбранных по какому-либо признаку, может быть универсально закодирована на основе методов символьной динамики. Несложно показать, что существует некоторая универсальная грамматика, определяющая разрешенные слова (последовательности унитарных кодов) или устойчивые периодические траектории, и запрещенные, определяющие конфликтные комбинации последовательностей унитарного кода, обрабатываемого ИКК. В этом смысле универсальность можно трактовать как принадлежность обрабатываемых ИКК последовательностей унитарного кода к одному универсальному классу, которые в области точек бифуркации будут иметь траектории одного вида. При этом точки бифуркации формируются и существуют в области пересечения траекторий (орбит вычислительных процессов). Можно предположить и обратное, что точки пересечения орбит вычислительных процессов формируют особые точки (точки бифуркации). Совершенно очевидно, что существует связь между этими особыми точками (точками изменения режима взаимодействия), их расположением на орбитах вычислительных процессов и метрическими свойствами конкретной реализации хаотического движения рабочей точки по дискриминационной поверхности^[13]. При этом хаотическое движение рабочей точки можно рассматривать как случайное блуждание между орбитами вычислительных процессов, каждая из которых вносит вклад в величину вероятности посещения. Тогда потенциальную опасность фрагмента кода можно трактовать как совокупность этих вероятностей, определяемых на основе пролонгации участка траектории движения рабочей точки, определяемого на каждом шаге обработки пакета (последовательности) унитарного кода.

 

Рис. 2.1. Структурно-функциональная схема типового элемента ИКК

 

При таком подходе типичный цикл функционирования выделенного элемента ИКК (рис.2.1) представляется в виде первичного анализа последовательности унитарных кодов x_ij^k, поступающей от i-го вынесенного объекта управления на j-м шаге функционирования на k-й уровень иерархии ИКК (уровни нумеруются снизу вверх по иерархии, начиная с 1). Это осуществляется оператором- дискриминатором D_k, задачей которого является выделение из входной последовательности некоторой вложенной последовательности x_ij^k_(m), которая обрабатывается соответствующей частной целевой функцией T_k^(m) с формированием выходной последовательности y_ij^k= T_k^(m)Ä x_ij^k_(m)Å y_ij^k+1, передаваемой на последующий (нижний) уровень иерархии (знаки Ä и Å отражают некоторые операции, выполняемые над потоком унитарных кодов). Оставшаяся часть последовательности x_ij^k+1, которая не может быть обработана на k-м уровне, передается на последующий верхний уровень иерархии для дальнейшей обработки.

Однако различие слов универсальной грамматики и распределений вероятностей, рассматриваемое на каждом шаге функционирования ИКК для каждого пакета (выделенной последовательности унитарного кода) без учета динамики изменения на последующем шаге, не может быть использовано в качестве критерия опасности (наличия запрещенных слов). Определение типа или прогноз изменения установившегося режима взаимодействия могут быть осуществлены только при пролонгации изменения вероятности реализации целевой функции ИКК на весь интервал взаимодействия при j→∞ на основе конечного набора имеющихся значений вероятности (набора запрещенных и разрешенных слов). Такая оценка при ее получении на начальном этапе взаимодействия в условиях значительной априорной неопределенности поведения системы постоянно уточняется до достижения заданной достоверности прогноза.

Такой подход может быть реализован на основе математического аппарата теории случайных блужданий, построенной на базе методов гармонического анализа и теории потенциала, применяемых на целочисленной решетке евклидова пространства, и направленной на определение некоторых функционалов траектории случайного движения рабочей точки (блуждания, универсальной грамматики).

Пронумеровав используемые в ИКК частные целевые функции неотрицательными целыми числами, можно рассматривать последовательность их реализаций при обработке входного потока унитарных кодов как движение изображающей точки в одномерном евклидовом пространстве. Такое движение является пространственно однородным и устойчивым, что позволяет рассматривать последовательность реализаций частных целевых функций ИКК как случайное блуждание с переходной функцией P(x,y), определенной для всех пар x и y точек неотрицательной полуоси R этого одномерного евклидова пространства и обладающей свойствами, которые могут трактоваться как требования

 

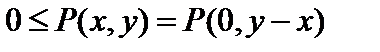, (2.1)

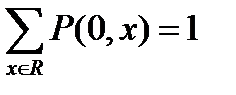. (2.2)

Требование (2.1) отражает свойство пространственной однородности, в соответствии с которым переходная функция случайного блуждания является функцией одного переменного (или может быть сведена к нему) p(x)=P(0,x) со свойствами

.

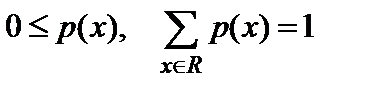Выбор переходной функции эквивалентен, таким образом, заданию на R вероятностной меры, то есть неотрицательной функции p(x), сумма значений которой по всем точкам из R равна 1. При этом требование пространственной однородности случайного блуждания, которое является единственным ограничением рассматриваемого подхода, полностью реализуется для реальных ИКК, так как в процессе функционирования не существует целевых функций с особыми привилегиями или приоритетами[14].

Вероятность P(0,x) в этом случае можно рассматривать как вероятность перехода за один шаг из состояния реализации частной целевой функции «0» в состояние выполнения частной целевой функции x. Тогда P_n(0,x) представляет собой вероятность перехода за n шагов, то есть вероятность того, что после n шагов функционирования, определяемых переходной функцией P(x,y), в ИКК будет реализовываться x-я частная целевая функция. Учитывая, что до поступления входной последовательности в ИКК реализовывалась некоторая вполне определенная частная целевая функция, можно утверждать, что

,

где δ(x,y) – дельта-функция Дирака).

Тогда, обозначив 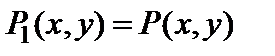, для n-го шага несложно получить

.

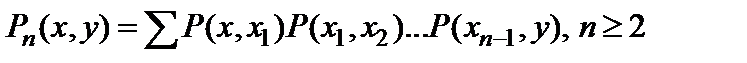В этом выражении суммирование выполняется по всевозможным наборам x₁,x₂,...,x_n-1 точек из R, откуда следуют выражения для вероятности реализации (m=y-x)-й частной целевой функции на (n+m)-м шаге взаимодействия:

,

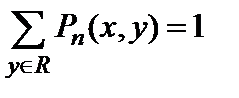, (2.3)

.

В условиях конфликтного функционирования ИКК представляет интерес вероятность того, что некоторая (например, запрещенная в условиях бесконфликтного функционирования) частная целевая функция или их комбинация будет реализована на n-м шаге впервые. В отличие от P_n(x,y), эта вероятность не является переходной функцией и не может быть определена в рамках разрешенной универсальной грамматики символьной динамики ИКК. Тогда вероятность F_n(x,y)того, что случайное блуждание, находясь в момент времени t=0 в точке x, впервые попадет в точку y в момент времени t=n, определяется как

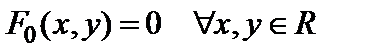
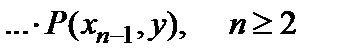, (2.4)

где символом {y} обозначено подмножество пространства R, состоящее из одного элемента {y}, а выражение R–{y} обозначает дополнение к {y}.

При этом несложно показать, что для 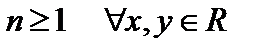выполняются рекуррентные соотношения и граничные условия

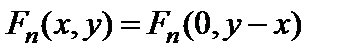
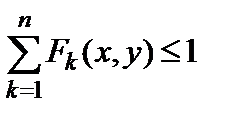
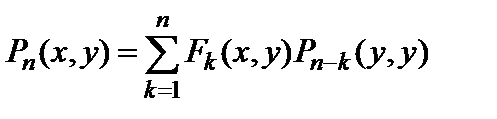. (2.5)

Для определения системы критериев возвратности случайного блуждания, позволяющих определить принципиальную возможность пролонгации характеристик конкретного ИКК, целесообразно ввести величину G_n(x,y), определяющую ожидаемое число переходов случайного блуждания в точку y при начальной точке блуждания x за время (число шагов) n. Это безразмерное время определяется длиной обрабатываемых ИКК последовательностей унитарных кодов, из которой без каких-либо принципиальных трудностей могут быть выделены отдельные фрагменты для их анализа совместно с аналогичными фрагментами других пакетов. Аналогично выделяются особые последовательности из вновь образованной последовательности унитарных кодов, что позволяет реализовать принцип последовательного рассмотрения выделенных последовательностей в нескольких слоях, обусловленных изменением состояния ИКК за счет обработки прошедшего пакета. Число этих слоев может быть произвольно большим и определяется сходимостью полученной оценки. При этом несложно показать, что

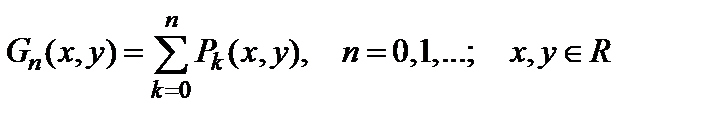, (2.6)

а в пределе при n→∞, введя обозначение

,

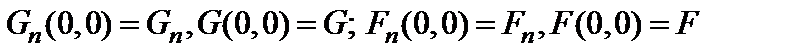имеют место соотношения

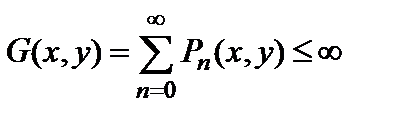, . (2.7)

При этом оценки на n-м шаге величины G можно выразить как

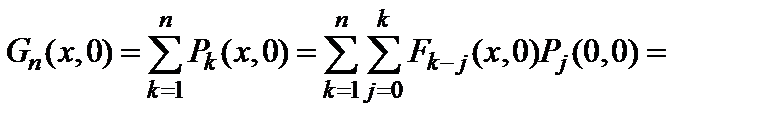
(2.8)

Отсюда в соответствии с выражением (2.7) можно определить возвратное блуждание как такое, при котором

,

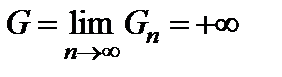а невозвратное – при котором

.

Таким образом, при невозвратном блуждании в пределе (при достаточно большом числе шагов) имеет место срыв (или, по крайней мере, чрезвычайно большая временная задержка) цикла, в то время как при возвратном блуждании число возвратов в исходное состояние для начала нового цикла сохраняется. При этом можно отметить, что при возвратном случайном блуждании (циклическом функционировании ИКК) за достаточно большое время (число шагов) реализуются все частные целевые функции комплекса, то есть имеет место отсутствие информационной избыточности.

Более строго, во множестве частных целевых функций ИКК можно выделить три образующих универсальную грамматику подмножества S, R⁺ и R⁻, формально определяемых как

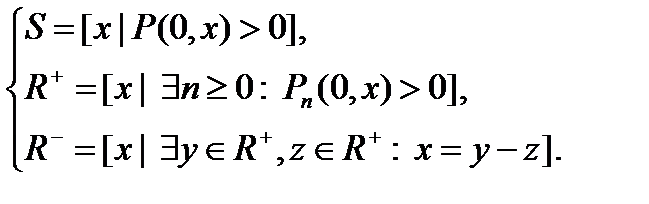(2.9)

Подмножество S состоит из разрешенных слов и их сочетаний универсальной грамматики (траекторий движения рабочей точки, орбит вычислительных процессов) частных целевых функций ИКК[15]. Подмножество R⁺ состоит из последовательностей реализованных до n-го шага разрешенных частных целевых функций. Подмножество R⁻ включает все элементы универсальной грамматики (как разрешенные, так и запрещенные), то есть все последовательности реализованных до n-го шага частных целевых функций комплекса. При этом несложно показать, что R⁺ является множеством всех конечных сумм элементов из S, включая 0 (пустую сумму), а также является наименьшей аддитивной подгруппой, содержащей S, а R⁻ является наименьшей аддитивной подгруппой в R, содержащей R⁺.

Система множеств (2.9) описывает информационную избыточность существующих ИКК, которая в данной работе понимается в смысле существования в системе «лишних» частных целевых функций, то есть функций, не реализуемых в процессе функционирования за период наблюдения. Соответственно, в системе без избыточности все частные целевые функции ИКК реализуются хотя бы раз в процессе функционирования за достаточно большое, но конечное число шагов интервала мониторинга.

Для систем без избыточности R=R⁻ и соответствующее случайное блуждание P(x,y), определенное на R, является апериодическим. При этом периодическое блуждание всегда можно свести к апериодическому путем выбора другой группы R размерности 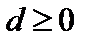, изоморфной R⁻, что соответствует устранению избыточности ИКК. Это позволяет, не снижая общность подхода, ограничиться рассмотрением апериодических случайных блужданий, соответствующим ИКК без информационной избыточности. Для этого случая случайного блуждания с переходной функцией P(x,y) имеют место соотношения

G(0,x)<∞ на R, F(0,0)<1, F(0,x)=0 на R–R⁺

для невозвратного блуждания и для возвратного блуждания

G(0,x)=∞ на R, F(0,x)=1 на R.

При рассмотрении конфликтного функционирования ИКК пролонгация изменения вероятности реализации целевой функции возможна лишь для возвратных случайных блужданий, при которых сохраняется циклическое функционирование комплекса. В этом случае представляется возможным сформировать определенную количественную «меру возвратности» случайного блуждания на основе сравнения количества «попаданий» случайного блуждания в исходную точку (то есть в начало цикла) с количеством «попаданий» в другие точки (располагающиеся внутри цикла):

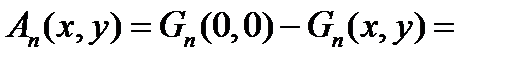
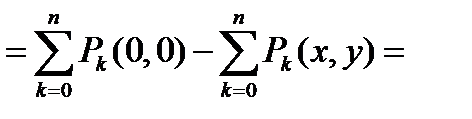
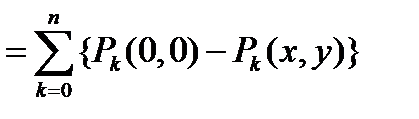. (2.10)

При этом практический интерес с точки зрения пролонгации характеристик функционирования ИКК представляет предел подобной меры на достаточно большом интервале функционирования, то есть при . Соответствующий предел определяется как

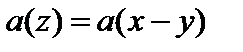
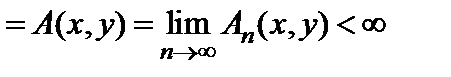(2.11)

и известен в литературе как ядро потенциала случайного блуждания.

Обозначив ядро потенциала текущего режима функционирования ИКК через

,

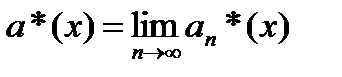на основе предельного тождества для ядра потенциала конфликтного взаимодействия можно утверждать, что мерой «конфликтности» текущего режима функционирования ИКК является «удаленность» ядра потенциала a*(x) (или его оценки a_n*(x)) от ядра потенциала a(x) (или оценки a_n(x)) бесконфликтного функционирования, нормированная величиной «удаленности» ядра потенциала a(x) от 0. Учитывая дискретность и ограниченность сверху и снизу аргумента x потенциалов, в качестве количественной меры такой удаленности можно ввести понятие показателя конфликтности

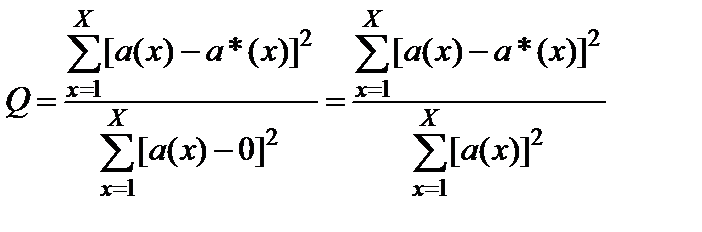, (2.12)

где X – размерность множества индексов {x}, то есть количество частных целевых функций, реализованных в ИКК.

Показатель конфликтности Q имеет достаточно очевидную физическую интерпретацию, определяемую его свойствами:

Ø если a(x)≡a*(x), то есть потенциалы тождественны, Q=0,

Ø если a*(x)≡0, то Q=1,

Ø в остальных случаях 0<Q<1.

Таким образом, коэффициент конфликтности Q будет определять меру конфликтности текущего режима функционирования ИКК, что эквивалентно в рассматриваемом контексте мере конфликтности фрагмента унитарного кода, поступающего или обрабатываемого ИКК. Значения Q, близкие к 0, соответствуют бесконфликтному функционированию, Q≈1 означает наличие взаимно исключающих целей при взаимодействии, то есть реализации конкретной последовательности унитарного кода. При этом следует отметить, что при анализе режима функционирования ИКК с потенциально конфликтным компонентом, сигнатура которого неизвестна, не представляется возможным определить точное значение предела (2.11) и, соответственно, применить соотношение (2.12). В этом случае целесообразно использовать оценки ядер потенциалов, для которых оценка коэффициента конфликтности на произвольном n-м шаге взаимодействия имеет вид

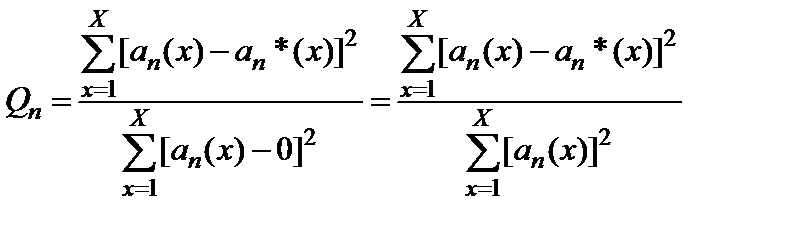. (2.13)

Аппаратная реализация предложенного алгоритма идентификации на основе оценки показателя конфликтности фрагмента унитарного кода может быть выполнена на основе инкрементного побитового накопления с одновременным анализом (рис.2.2). При этом блок идентификации всегда реализует попытку анализа принятого участка последовательности длиной k бит, при k³1. Анализ осуществляется посредством применения к последовательности операции информационной свертки, выделяющей из последовательности обращения (вызовы) к частным целевым функциям ИКК и точкам входа в критические приложения, причем применяемая свертка должна быть тождественна по своей реализации используемой в ИКК для декодирования входного потока.

 

Рис.2.2. Структурно-функциональная схема блока определения показателя конфликтности

 

В случае если длина k анализируемого участка последовательности недостаточна для анализа (например, в силу невозможности декодирования частично принятого пакета), последовательность буферизуется в блоке идентификации и одновременно передается в ИКК. При этом в силу тождественности применяемых сверток можно с уверенностью утверждать, что переданная в ИКК последовательность также не будет успешно декодирована и исполнена, то есть потенциально опасный фрагмент унитарного кода, содержащийся в принятой последовательности унитарных кодов, не будет реализован в текущем вычислительном процессе.

В случае если принимаемая последовательность содержит потенциально опасный фрагмент унитарного кода, в простейшем случае принимается решение о блокировании пакета в пределах блока идентификации, при этом выделенный фрагмент не реализуется в информационном пространстве ИКК. Если же последовательность не содержит конфликтного компонента, ее последний k-й бит пропускается на вход ИКК, после чего осуществляется декодирование принятой последовательности и исполнение в информационном пространстве комплекса. При этом происходит пересчет текущего значения ядра потенциала случайного блуждания на основании реально имевших место реализаций частных целевых функций ИКК.

Используя введенный выше показатель конфликтности (или «меру конфликтности») взаимодействия ИКК, с формальной точки зрения в качестве целевой функции управления средствами защиты информации целесообразно использовать

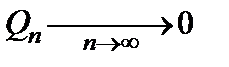, (2.14)

представляющее собой условие снятия конфликта за достаточно большое число шагов взаимодействия. С учетом определений (2.12) и (2.13), можно определить физический смысл (2.14) как требование к уменьшению различия ядер потенциалов эталонного (бесконфликтного) режима функционирования и текущего режима с увеличением времени взаимодействия. Условие (2.14) можно рассматривать и как условие информационной устойчивости системы.

Выражение (2.14) представляет собой в некотором смысле «идеальное» условие полного снятия конфликта за достаточно большой временной интервал взаимодействия. Применительно к взаимодействию реальных ИКК целесообразно говорить о сохранении некоторого заданного (не обязательно нулевого) уровня конфликтности взаимодействия, достижимого на данном этапе взаимодействия с учетом объективных ограничений. При этом требование бесконфликтного режима взаимодействия соответствует небольшим (точнее, наименьшим возможным) значениям коэффициента конфликтности Q, то есть Q<<1, Q≈0.

Для проверки приведенного подхода для определения потенциальной опасности обрабатываемого фрагмента был проведен расчет оценок ядер потенциала для различного числа шагов n при обработке заведомо конфликтных и бесконфликтных пакетов. Результаты этих расчетов приведены на рис.2.3.

бесконфликтное функционирование	конфликтное функционирование
Рис. 2.3. Значение ядра потенциалов случайных блужданий при взаимодействии ИКК

Даже поверхностный анализ приведенных зависимостей показывает, что с увеличением числа шагов при обработке потока унитарного кода в случае бесконфликтного взаимодействия (рис.2.3) величина ядра потенциала случайного блуждания стабилизируется в области 0,5 с увеличением числа шагов n. При этом, поскольку коэффициент конфликтности, практически, представляет числовой дифференциал дискретной функции изменения величины ядра потенциала случайных блужданий, то в этом случае коэффициент конфликтности (потенциальной опасности) обрабатываемого пакета унитарного кода стремится к 0. Для конфликтного функционирования аналогичные оценки величины ядра потенциала монотонно убывают с увеличением времени функционального взаимодействия, что обуславливает рост коэффициента конфликтности (потенциальной опасности) обрабатываемого или исполняемого кода. Полученные зависимости свидетельствуют, таким образом, о достаточно быстрой сходимости оценки (2.13) в соответствии с целевой функцией (2.14), что позволяет использовать оценки ядер потенциалов вместо точных значений соответствующих пределов.

Таким образом, представленный подход позволяет в условиях априорно неизвестных сигнатур информационных воздействий проводить их выявление независимо от их источника и окружения в потоке унитарного кода. Аппаратная реализация приведенного алгоритма также не представляет трудности на основе, например, сигнальных процессоров, обеспечивающих обработку потоков унитарного кода при выявлении потенциально опасных фрагментов при скоростях информационного обмена до 50-100 Мбит/с.