Векторные и матричные операторы

Введем обозначения: V1, V2 – векторы, M – матрица, Z – скаляр. Пусть V1 := ,
V2 := , M := , M1 := , Z = 5.

V1 + V2 = – операция сложения векторов V1 и V2.

V1 - V2 = - операция вычитание вектора V2 из вектора V1.

-V2 = – операция смена знаков у элементов вектора V2.

V1 – Z = – операция вычитания скаляра Z из всех элементов вектора V1.

- М = 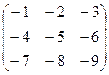- операция смены знаков у элементов матрицы М.

Z*V1 = или V1*Z = – задание скалярного произведения вектора V1 на скаляр Z.

Z*M = 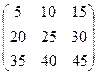или M*Z = 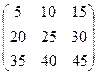– задание скалярного произведения матрицы М на скаляр Z.

V1*V2 = 32 – операция скалярного умножения двух векторов V1 и V2.

М*V2 = - операция скалярного умножения матрицы М на вектор V2.

М*М1 = – операция скалярного умножения двух матрицы М1 и М2.

V1/Z = – операция деления всех элементов вектора V1 на скаляр Z.

M/Z = – операция деления матрицы М на скаляр Z.

M^3 = – операция возведение матрицы М в степень 3.

M^-1 = – операция обращения матрицы М, т.е. нахождение обратной матрица.

|V1 = 3.762 – операция вычисление модуля вектора |V1|.

|M = 0 – операция вычисления определителя матрицы М.

V1 Ctrl ! = (1, 2, 3) – транспонирование вектора V1.

M Ctrl ! = – транспонирование матрицы М.

V1 Ctrl * V2 = = – векторное умножение двух векторов V1 и V2.

V1 Ctrl - = - векторизация вектора V1, т.е.одновременное проведение некоторой скалярной операции над всеми элементами вектора или матрицы.

M Ctrl - = – векторизация матрицы М.

M Ctrl ^ 2 = 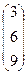– выделение 2 – го столбца матрицы М.

V1 [ 2 = 3 – выделение 2 – го элемента вектора V1.

M [1,1 = 5 – выделение элемента (1,1) матрицы М.

Символ [ - это прямая, открывающаяся скобка используется для ввода индекса элемента массива или вектора.

. – точка используется для ввода индекса скалярной переменной, причем синий уголок курсора ввода должен охватывать все имя переменной, а не только область ввода.