Сложение и вычитание приближенных чисел

Рассмотрим задачу: сложить приближенные числа 2.389, 17.2, 8.65 и 94.12. Первое слагаемое содержит 9 тысячных долей. С чем их складывать? Ведь остальные слагаемые тоже содержат какие-то тысячные доли, но нам они неизвестны. Неизвестно, так же, сколько сотых у второго слагаемого. Десятые доли даны у всех слагаемых, их сумму легко найти. Поэтому все разряды правее десятых мы складывать не можем (не с чем), их мы отбрасываем, а десятые округляем обычным способом.

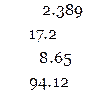
После сложения получим 122.4.

Итак, при сложении приближенных чисел сохраняем справа только те разряды, которые имеются у всех без исключения слагаемых, остальные десятичные знаки отбрасываем с округлением.

Аналогично поступаем и при вычитании. Например,

.

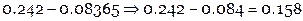Отметим одну неприятную особенность вычитания приближенных чисел. Если вычитаются близкие числа, имеющие много верных цифр, то в результате может получаться число очень грубо приближенное. Например,

84.36-84.25=0.11, то есть вычитая числа с 4-мя значащими цифрами, получаем результат с 2-мя значащими цифрами. Именно по этой причине вычисления стараются строить так, чтобы избежать вычитания близких чисел.

Если избежать вычитания двух близких величин невозможно, то их надо брать с достаточно высокой точностью.

Отметим, что при сложении и вычитании приближенных чисел абсолютные погрешности слагаемых складываются.

Пример

Получить результат с 3-мя верными цифрами:

 

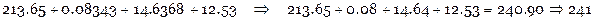
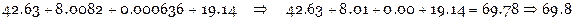
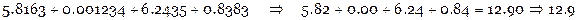
Получить результат с 2-мя верными цифрами:

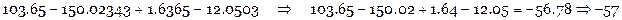
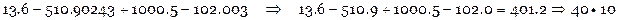
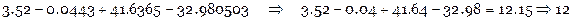
Сложить приближенные числа с наибольшей возможной точностью и оценить абсолютную и относительную погрешность результата:

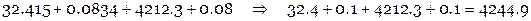
абс. погрешность 0.1

отн. погрешность 0.002%