Бегущей волной называется волна, которая переносит в пространстве энергию.

Тогда смещение всех частиц среды для бегущей волны будет:

.

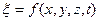(13.1)

Будем рассматривать плоскую волну, имеющую гармонический характер, распространяющуюся в положительном направлении оси х.

Пусть в начальный момент времени t смещение х = 0. Тогда

.

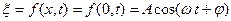(13.2)

Пусть через время t плоская волна приходит в точку с координатой х, а распространяется со скоростью V.

Тогда:

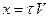	;	(13.3)
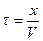	;	(13.4)
	.	(13.5)

Уравнение (13.5) является уравнением плоской волны, распространяющейся в положительном направлении оси х.

Зафиксируем какое-либо значение фазы колебания. Пусть фаза колебания является постоянной.

Сначала выразим время t, а затем продифференцируем это выражение по времени:

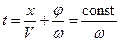	;	(13.6)
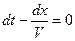	;	(13.7)
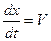	.	(13.8)

Из уравнения (13.8) следует, что V – скорость перемещения фазы волны (фазовая скорость).

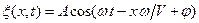	,	(13.9)
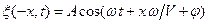	.	(13.10)

Волновое число k определяется соотношением (13.11).

,

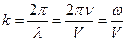(13.11)

.

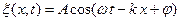Распространение волн в однородной изотропной среде, в общем случаи, записывается уравнением в частных производных:

.

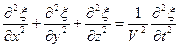(13.12)

Уравнение (13.12) – волновое уравнение в частных производных.

,

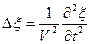(13.13)

где D – оператор Лапласа, .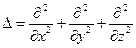

 

Пусть r – расстояние от центра волны до рассматриваемой точки среды. Тогда:

,

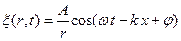(13.14)

уравнение сферической волны.