Задание по курсовому проекту
(практическая часть)
По территориям региона приводятся данные за 2014 год. Требуется:
1. Построить линейное уравнение парной регрессии y от x.
2. Рассчитать линейный коэффициент парной корреляции и среднюю ошибку аппроксимации.
3. Оценить статистическую значимость параметров регрессии и корреляции с помощью F-критерия Фишера и t-критерия Стьюдента.
4. Выполнить прогноз заработной платы y при прогнозном значении среднедушевого прожиточного минимума x, составляющем 107% от среднего уровня.
5. Оценить точность прогноза, рассчитав ошибку прогноза и его доверительный интервал.
6. На одном графике построить исходные данные и теоретическую прямую.
Вариант № 5
| Номер региона | Среднедушевой прожиточный минимум в день одного трудоспособного, руб., x | Среднедневная заработная плата, руб., y |
Решение:
Далее находим коэффициенты постулируемого уравнения регрессии, а также коэффициент корреляции. Для этого можно воспользоваться следующими формулами:
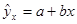


 ,
,
где: σх, σу – среднеквадратические отклонения от средних х и у.
Определим ряд характеристик моделируемых рядов:



Рассчитаем коэффициенты регрессии:


Таким образом, регрессионное уравнение имеет следующий вид:

С увеличением среднедушевого прожиточного минимума на 1 руб. среднедневная заработная плата возрастает в среднем на 0,9 руб.
Уравнение линейной регрессии всегда должно дополняться показателем тесноты свзи – линейным коэффициентом корреляции:

Близость коэффициента корреляции rxy к единице указывает на тесную линейную связь между признаками.
Далее для оценки качества подбора линейной функции рассчитывается коэффициент детерминации rxy2.
Коэффициент детерминации характеризует долю дисперсии результативного признака y в общей дисперсии результативного признака:

Коэффициент детерминации показывает, что уравнением регрессии объясняется 62% дисперсии результативного признака.
Величина (1-rxy2) – характеризует долю дисперсии y, вызванную влиянием остальных факторов, не учтенных в модели, что составляет 38%.
Далее, дополним таблицу 2, следующими вычислениями:
Таблица 2.
| № | x | y | X² | x·y | y² | ŷ | (y-ŷ) | (y-ŷ)² | (ŷ-yср)² | A | |А| |
| 132,08 | 4,92 | 24,21 | 106,85 | 3,59 | 3,59 | ||||||
| 136,78 | 5,22 | 27,25 | 31,77 | 3,68 | 3,68 | ||||||
| 124,56 | 3,44 | 11,83 | 318,86 | 2,69 | 2,69 | ||||||
| 137,72 | 2,28 | 5,20 | 22,06 | 1,63 | 1,63 | ||||||
| 133,96 | -0,96 | 0,92 | 71,52 | -0,72 | 0,72 | ||||||
| 128,32 | 24,68 | 609,10 | 198,72 | 16,13 | 16,13 | ||||||
| 130,20 | 11,8 | 139,24 | 149,25 | 8,31 | 8,31 | ||||||
| 145,24 | 8,76 | 76,74 | 7,97 | 5,69 | 5,69 | ||||||
| 128,32 | 3,68 | 13,54 | 198,72 | 2,79 | 2,79 | ||||||
| 138,66 | 11,34 | 128,60 | 14,11 | 7,56 | 7,56 | ||||||
| 133,02 | -1,02 | 1,04 | 88,30 | -0,77 | 0,77 | ||||||
| 159,34 | 6,66 | 44,36 | 286,40 | 4,01 | 4,01 | ||||||
| Сумма | 1628,20 | 80,8 | 1082,02 | 1494,51 | 57,57 | ||||||
| Среднее | 86,83 | 142,42 | 7629,7 | 12447,3 | 20399,9 | 135,68 | 4,80 | ||||

| 9,47 | 10,84 | |||||||||

| 89,64 | 117,41 |
Далее проведем оценку значимости уравнения линейной регрессии в целом, так и отдельных его параметров.
Чтобы иметь общее представление о качестве модели из относительных отклонений по каждому наблюдению определяют среднюю ошибку аппроксимации.

Считается, что модель является приемлемой, если величина ошибки аппроксимации не превышает 10%, следовательно, полученная регрессионная зависимость достаточно хорошо описывает анализируемые данные, поскольку величина  .
.
Оценка значимости уравнения регрессии в целом проводится на основе F-критерия Фишера.
Рассчитаем фактическое значение F-критерия Фишера:

Фактическое значение F-критерия Фишера сравнивается с табличным значением.
По таблице F-распределения Снедекора-Фишера при α = 0,05 и К1 = 1, К2 = 12 – 2 = 10 величина Fт = 4,96. Это означает, что гипотеза Н0 о несущественности связи между y и x с вероятностью ошибочности суждения α = 0,05 отклоняется, то есть связь между этими переменными может быть признана существенной.
В парной линейной регрессии оценивается значимость не только уравнения в целом, но и отдельных его параметров.
Далее рассчитаем по каждому из параметров его стандартные ошибки ma и mb.


 =0,32
=0,32
Величина стандартной ошибки с t-распределением Стьюдента при (n-2) степенях свободы применяется для проверки существенности коэффициента регрессии и для нахождения его доверительного интервала.
Для оценки существенности коэффициента регрессии его величина сравнивается с его стандартной ошибкой, т.е определяется фактическое значение t-критерия Стьюдента:
 ;
;  ;
; 
Фактическое значение t-критерия Стьюдента необходимо сравнить с табличным значением t-критерия Стьюдента при определенном уровне значимости и числе степеней свободы (n-2).
Фактическое значение t-статистик составляет:
 ;
;
 ;
;

Табличные значения t-критерия Стьюдента при α=0,05 и числе степеней свободы =n-2=10, составляет
tтабл = 1,812
Таким образом, все коэффициенты регрессии и коэффициент корреляции оказались значимы, так как расчётные значения t-критерия выше табличного значения. Так как , t(a) > t(таб), t(b ) > t (таб) и t (r) > t(таб) , то признаем статистическую значимость параметров регрессии и показателя тесноты связи.
Далее рассчитаем доверительные интервалы для параметров регрессии a и b:
a ± t*m(a) и b ± t*m(b)
Подставив значения получим:
| а ± | 61,78 |
| b± | 0,71 |
| r± | 0,44 |
аϵ[64,21-61,78; 64,21+61,78]=[2,43; 125,99]
bϵ[0,9-0,71; 0,9+0,71]=[0,19; 1,61]
Анализ верхней и нижней границ доверительных интервалов приводит к выводу о том, что с вероятностью p = 1 - α = 0,95 параметры a и b , находясь в указанных границах, не принимают нулевых значений, т.е. не являются статистически незначимыми и существенно отличны от нуля.
В прогнозных расчетах по уравнению регрессии определяется предсказываемое yp значение как точечный прогноз, то есть путем подстановки в уравнение регрессии yx=a+b*x, соответствующего значения x.
| x(р) =1,07*x (ср) = | 92,91 |
| y(р) =54,06+0,94*x( р) = | 147,89 |
Но точечный прогноз не реален, его необходимо дополнить расчетом стандартной ошибки и интервальной оценкой прогнозного значения.
y(р)-∆ ≤ y(р) ≤ y(р)+∆
Ошибка прогноза составит:
m(у(р)) = σост*(√1+1/n+((xp-xcp)²/(∑(x-xcp)²))=10,8268
∆ = σост*(√(1+(1/n)+((xр+xср)²/(n* σ²)) =1,95587
Доверительный интервал (y(р)-∆ ≤ y(р) ≤ y(р)+∆) составит:
147,89-1,95587< y(р)<147,98+1,95587
145,94≤y(р)≤ 149,85
Прогноз является статистически значимым.
Теперь на одном графике изобразим исходные данные и линию регрессии:
