Билет 20.

 

1. РЕШЕНИЕ НЕЛИНЕЙНЫХ УРАВНЕНИЙ: ПОСТАНОВКА ЗАДАЧИ, ШАГОВЫЙ МЕТОД.

2. Перевести A₂=101110,101_2, A₈=125,46_8, A₁₆=2AF,C4₁₆ в десятичное. Выполнить перевод числа 0,847 в двоичную систему счисления

Уравнение типа F(x)=0 или x=f(x) называется нелинейным. Решить уравнение это значит найти такое x, при котором уравнение превращается в тождество. В общем случае уравнение может иметь 0; 1; 2;...∞ корней. Рассмотренные ниже численные методы решения нелинейных уравнений позволяют находить один корень на заданном интервале [a,b]. При этом на интервале должен существовать только один корень. Рассмотрим несколько методов решения нелинейных уравнений.

1.Метод перебора. При решении нелинейного уравнения методом перебора задаются начальное значение аргумента x=a и шаг h, который при этом определяет и точность нахождения корней нелинейного уравнения. Пока выполняется условие F(x)*F(x+h)>0 аргумент x увеличиваем на шаг h (x=x+h). Если произведение F(x)*F(x+h) становится отрицательным, то на интервале [x,x+h] существует решение уравнения. Пока F(x)∙F(x+h)>0 x=x+h

 

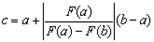3.Метод хорд. При решении нелинейного уравнения методом хорд задаются интервал [a,b], на котором существует только одно решение, и точность ε. Затем через две точки с координатами (a,F(a)) и (b,F(b)) проводим отрезок прямой линии (хорду) и определяем точку пересечения этой линии с осью абсцисс (точка c). Если при этом F(a)∙F(c)<0, то правую границу интервала переносим в точку с (b=c). Если указанное условие не выполняется, то в точку c переносится левая граница интервала (а=с). Поиск решения прекращается при достижении заданной точности |F(c)|< ε. Для определения точки пересечения хорды с осью абсцисс воспользуемся следующей формулой (попытайтесь получить формулу самостоятельно). Пока |F(c)|>ε

F(a)∙F(c)<0

4.Метод касательных. При решении нелинейного уравнения методом касательных задаются начальное значение аргумента x0 и точность ε. Затем в точке(x0,F(x0)) проводим касательную к графику F(x) и определяем точку пересечения касательной с осью абсцисс x1. В точке (x1,F(x1)) снова строим касательную, находим следующее приближение искомого решения x2 и т.д. Указанную процедуру повторяем пока |F(xi)| > ε. Для определения точки пересечения (i+1) касательной с осью абсцисс воспользуемся следующей формулой 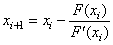Условие сходимости метода касательных F(x0)∙F''(x0)>0. Пока |F(x)|> ε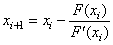

5.Метод хорд-касательных. Если в методе касательных производную функции F'(xi) заменить отношением конечных приращений, то получаем расчетную формулу для метода хорд-касательных . Порядок выполнения вычислений в данном методе аналогичен рассмотренному ранее.

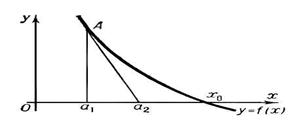
6. Метод итераций. При решении нелинейного уравнения методом итераций воспользуемся записью уравнения в виде x=f(x). Задаются начальное значение аргумента x0 и точность ε. Первое приближение решения x1 находим из выражения x1=f(x0), второе - x2=f(x1) и т.д. В общем случае i+1 приближение найдем по формуле xi+1 =f(xi). Указанную процедуру повторяем пока |f(xi)|>ε. Условие сходимости метода итераций |f'(x)|<1. Пока |f(xi)|> ε xi+1 =f(xi)

7.Шаговый метод. Пусть имеется уравнение F(x)=0, причем можно считать, что все интересующие вычислителя корни находятся на отрезке [А; В], в котором функция F(x) определена, непрерывна и F(A)*F(B)< 0. Требуется отделить корни уравнения, т. е. указать все отрезки [а; b] [А; B], содержащие по одному корню. Будем вычислять значения F(x), начиная с точки х=А, двигаясь вправо с некоторым шагом h. Как только обнаружится пара соседних значений F(x), имеющих разные знаки, и функция f(x) монотонна на этом отрезке, так соответствующие значения аргумента х (предыдущее и последующее) можно считать концами отрезка, содержащего корень.