Задание 3. Транспортная задача.

Решите транспортную задачу по имеющимся данным (в левых верхних углах клеток таблицы указаны стоимости перевозок единицы сырья соответствующему потребителю).

Имеются три пункта поставки однородного груза А₁, А₂, А₃ и пять пунктов В₁, В₂, В₃, В₄, В₅ потребления этого груза. На пунктах А₁, А₂ и А₃ находится груз соответственно в количестве а₁, а₂ и а₃ тонн. В пункты В₁, В₂, В₃, В₄, В₅ требуется доставить соответственно b₁, b₂, b₃, b₄ и b₅ тонн груза. Расстояние между пунктами поставки и пунктами потребления приведено в следующей матрице- таблице:

Пункты поставки	Пункты потребления
	В₁	В₂	В₃	В₄	В₅
А₁	d₁₁	d₁₂	d₁₃	d₁₄	d₁₅
А₂	d₂₁	d₂₂	d₂₃	d₂₄	d₂₅
А₃	d₃₁	d₃₂	d₃₃	d₃₄	d₃₅

Найти план закрепления потребителей за поставщиками однородного груза, чтобы общие затраты по перевозкам были минимальными. Составить математическую модель задачи и решить ее, используя поиск решения таблиц EXCEL

а₁=150

а₂=150

а₃=200

b₁=100; b₂=70; b₃=130; b₄=110; b₅=90

D =

Решение

Найдем сумму запасов и сумму потребностей: a₁+a₂+a₃=150+150+200=800; b₁+b₂+b₃+b₄+b₅=100+70+130+110+90=500

Сумма запасов равна сумме потребностей, то есть все запасы должны быть вывезены, и все потребности удовлетворены.

Обозначим x_i_,_j–количество груза перевозимого от A_i к B_j и составим математическую модель задачи.

Целевая функция – общие затраты на перевозки

Z=20x₁₁+3x₁₂+9x₁₃+15x₁₄+35x₁₅+

+14x₂₁+10x₂₂+12x₂₃+20x₂₄+46x₂₅+

+ 25x₃₁+11x₃₂+16x₃₃+19x₃₄+48x₃₅→min.

Ограничения:

Найти неотрицательные значения x_i_,_j удовлетворяющие системе ограничений и минимизировать функцию z – затраты по перевозке.

Выполним последовательность действий для решения задачи, используя модуль Поиск решения.

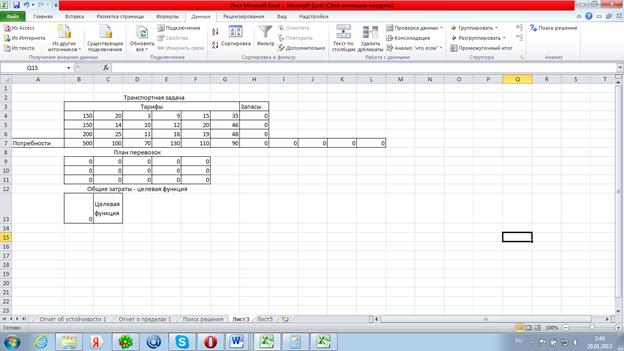
1. Записываем все данные в таблицу.

· В ячейку В2:Н2 запишем Транспортная задача

· В ячейку В3:G3 запишем Тарифы

· В ячейку Н3: Запасы

· Записываем в ячейку A7: Потребности

· В ячейки С4:G6 записываем матрицу перевозок D

· В ячейку В8:G8 запишем План перевозок

· Заносим 0 в блок ячеек B9:F11

В ячейку В12: F12 запишем Общие затраты -целевая функция

· В ячейку C13: Целевая функция

2. Записываем в ячейку B13 формулу =СУММПРОИЗВ(C4:G6;B9:F11)

3. В ячейку H4 записываем формулу =СУММ(B9:F9) и копируем ее в ячейки H5 и H6

4. В ячейку H7 записываем формулу =СУММ(B9:F9) и копируем ее в ячейки I7,J7,K7 и L7

5. Далее в Сервис-Поиск решения берем целевую функцию, min,поле для значений и ограничения, как показано на рисунке.

			Транспортная задача
	Тарифы	Запасы



Потребности
	План перевозок



	Общие затраты - целевая функция
		Целевая функция

Используемая литература:

1. Л.П. Бойченко, О.Н. Туманова. Экономико-математические методы и модели: Учебное пособие. – Ухта: УГТУ, 1999. – 125 с., ил.

2. Экономико-математические методы и прикладные модели: Учеб. пособие для вузов/ В.В. Федосеев, А.Н. Гармаш, Д.М. Дайитбегов и др.; Под ред. В.В. Федосеева. – М.: ЮНИТИ, 1999. – 391 с.