Вводя обозначения
 ,
,  , (10)
, (10)
можно записать выражение (9) в виде

 (11)
(11)
Как и в [35], рассмотрим вначале стационарное состояние  при
при  . Имеем
. Имеем
0 для 
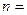
 , (12)
, (12)
1 -  для
для 
то есть при  молекулы
молекулы  отсутствуют, а при
отсутствуют, а при  поддерживается постоянная концентрация
поддерживается постоянная концентрация  . Этот переход из состояния «есть молекулы
. Этот переход из состояния «есть молекулы  » в состояние «нет молекул
» в состояние «нет молекул  » при варьировании
» при варьировании  похож на фазовый переход. Как и в [35,36], можно провести аналогию с уравнением ферромагнетизма, записав (11) при
похож на фазовый переход. Как и в [35,36], можно провести аналогию с уравнением ферромагнетизма, записав (11) при  в виде
в виде
 , (13)
, (13)
где отчетливо видны соответствия  в
в
 (14)
(14)
где  - намагниченность,
- намагниченность,  - магнитное поле,
- магнитное поле,  - абсолютная температура,
- абсолютная температура,  - критическая температура.
- критическая температура.
Теперь проведем изучение временной эволюции, следуя общепринятым методам [35-38]. В случае  задачу можно свести к решению уравнения
задачу можно свести к решению уравнения
 (15)
(15)
с начальными условиями
 , (16)
, (16)
 , (17)
, (17)
так что  асимптотически приближается к нулю.
асимптотически приближается к нулю.
В случае  Решение (15) с учетом (16) имеет вид
Решение (15) с учетом (16) имеет вид
 , (18)
, (18)
где
 , (19)
, (19)
а
 . (20)
. (20)
Видим, что при  решение (17) стремится к следующим равновесным значениям
решение (17) стремится к следующим равновесным значениям
 для
для 
 (21)
(21)  для
для 
Теперь рассмотрим случай  в (15). В этом случае его решение с учетом (16) имеет такой же вид, как и в (18). Но в этом случае коэффициент
в (15). В этом случае его решение с учетом (16) имеет такой же вид, как и в (18). Но в этом случае коэффициент  равен
равен
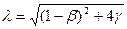 , (22)
, (22)
а  дается выражением типа (19).
дается выражением типа (19).
Из (18) и (22) следует, что концентрация  монотонно стремится к равновесному значению, а ее осцилляции отсутствуют.
монотонно стремится к равновесному значению, а ее осцилляции отсутствуют.
Проведем вкратце обсуждение полученных результатов. Посмотрим, что означает в нашем случае равенство  , представляющего равенство нулю трех слагаемых в (10). Равенства
, представляющего равенство нулю трех слагаемых в (10). Равенства  и
и  означают необратимость реакций (3) и (4), а равенство
означают необратимость реакций (3) и (4), а равенство  означает отсутствие производства
означает отсутствие производства  по реакции (2). Это может случиться либо при очень низких температурах, либо в условиях изоляции системы от атмосферы кислорода, так что
по реакции (2). Это может случиться либо при очень низких температурах, либо в условиях изоляции системы от атмосферы кислорода, так что  . Согласно (13), слой окисла
. Согласно (13), слой окисла  на поверхности кремния может претерпевать неравновесный фазовый переход типа (12), (21): либо
на поверхности кремния может претерпевать неравновесный фазовый переход типа (12), (21): либо  для
для  (активная фаза окисления) [34], либо
(активная фаза окисления) [34], либо  для
для  (пассивная фаза окисления кремния [34]). Из (10) нетрудно видеть, что этот переход определяется величиной константы скорости
(пассивная фаза окисления кремния [34]). Из (10) нетрудно видеть, что этот переход определяется величиной константы скорости  прямой реакции (3), так как концентрацию кремния можно считать постоянной (
прямой реакции (3), так как концентрацию кремния можно считать постоянной (  ) ввиду большого избытка. Величина
) ввиду большого избытка. Величина  существенно зависит от температуры. Таким образом, в определенном температурном интервале слой окисла
существенно зависит от температуры. Таким образом, в определенном температурном интервале слой окисла  на поверхности кремния либо может исчезать вовсе
на поверхности кремния либо может исчезать вовсе  , либо утончатся до величины
, либо утончатся до величины  для случая
для случая  Временная эволюция
Временная эволюция  (см. выражение (21)) также подтверждает этот практически важный вывод синергетического подхода к проблеме окисления кремния в атмосфере кислорода. Временная эволюция
(см. выражение (21)) также подтверждает этот практически важный вывод синергетического подхода к проблеме окисления кремния в атмосфере кислорода. Временная эволюция  при
при  , также подтверждает наличие изменения
, также подтверждает наличие изменения  , когда толщина слоя
, когда толщина слоя  стремится к равновесному значению
стремится к равновесному значению  а осцилляции
а осцилляции  отсутствуют (см. выражения (18) и (22)). Этот случай не что иное как обычная пассивная фаза окисления кремния в открытой системе кремний-кислород, наблюдаемая в условиях отсутствия термодинамического равновесия [34].
отсутствуют (см. выражения (18) и (22)). Этот случай не что иное как обычная пассивная фаза окисления кремния в открытой системе кремний-кислород, наблюдаемая в условиях отсутствия термодинамического равновесия [34].