Вывести дифференциальное уравнение свободных колебаний механической системы с одной степенью свободы. Изложить его решение. Дать определение изохронизма свободных колебаний.

- Определяем положение системы обобщенной координатой q, при равновесии .

Уравнение Лагранжа II рода:

(1).

Так как равновесие устойчиво, а возмущения малы, для Т и П воспользуемся выражениями: , . Находим: (2).

Подставляя (2) в уравнение (1), получим: , где: = const, круговая или циклическая частота, которая имеет размерность угловой скорости ( ).

- ОЛДУ II порядка с постоянными коэффициентами (3).

Характеристическое уравнение:

Постоянные и определяем из начальных условий: .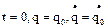

Частным решением уравнения (3), которое соотв. начальным условиям будет: .

Приведем решение к амплитудной форме: - закон движения системы.

- Величина периода, как и круговая частота, не зависят от начальных условий, а определяются только свойствами колеблющейся системы, то есть коэффициентом инерции и коэффициентом жесткости. Независимость периода и частоты колебаний от начальных условий называется изохронностью колебаний.

Линейное сопротивление и диссипативная функция. Доказать приближенную формулу диссипативной функции системы с одной степенью свободы при малых отклонениях от положения устойчивого равновесия.

Диссипативная функция Релея: (1)

Радиус-вектор каждой точки системы зависит только от обобщенной координаты q(t): . , следовательно, .

B(q) разложим в степенной ряд в окрестности положения равновесия ( ):

, а затем учтем в этом разложении только первый член, так как диссипативная функция Релея уже содержит в себе величину второго порядка малости . Обозначим этот член через «b», который назовем обобщенным коэффициентом сопротивления. Размерность коэффициента сопротивления зависит от размерности обобщенной координаты.

Окончательно приближенное значение диссипативной функции Релея: .