Методы замены.

 

Сущность методов замены (подстановки) заключается в замене символов исходной информации, записанных в одном алфавите, символами из другого алфавита по определенному правилу . Самым простым является метод прямой замены. Символам s_0i исходного алфавита A₀, с помощью которых записывается исходная информация, однозначно ставятся в соответствие символы s_1i шифрующего алфавита А₁. В простейшем случае оба алфавита могут состоять из одного и того же набора символов. Например, оба алфавита могут содержать буквы русского алфавита.

Задание соответствия между символами обоих алфавитов существляяется с помощью преобразования числовых эквивалентов символов исходного текста Т₀, длиной – К символов, по определенному алгоритму.

Алгоритм моноалфавитной замены может быть представлен в виде последовательности шагов.

Шаг 1. Формирование числового кортежа L_0h путем замены каждого символа 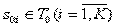, представленного в исходном алфавите A₀ размера [1xK], на число h_0i(s_0i), соответствующее порядковому номеру символа s_0i в алфавите A₀.

Шаг 2. Формирование числового кортежа L_1h путем замены каждого числа кортежа L_0h на соответствующее число h_1i кортежа L_1h, вычисляемое по формуле:

h_li=(k₁*h_0i(s_0i)+k₂)(mod R),

где k₁ – десятичный коэффициент; k₂ - коэффициент сдвига. Выбранные коэффициенты k₁, k₂ должны обеспечивать однозначное соответствие чисел h_0i и h_1i, а при получении h_1i=0 выполнить замену h_1i=R.

Шаг 3. Получение шифртекста Т₁ путем замены каждого числа h_li(s_li) кортежа L_1h соответствующим символом алфавита шифрования A₁ размера [1xR].

Шаг 4. Полученный шифртекст разбивается на блоки фиксированной длины b. Если последний блок оказывается неполным, то в конец блока помещаются специальные символы-заполнители (например, символ *).

Пример. Исходными данными для шифрования являются:

T₀=<М Е Т О Д _ Ш И Ф Р О В А Н И Я>;

A₀=<А Б В Г Д Е Ж З И К Л М Н О П Р С Т У Ф Х Ц Ч Ш Щ Ъ Ы Ь Э Ю Я _>;

A₁=<О Р Щ Ь Я Т Э _ Ж М Ч Х А В Д Ы Ф К С Е З П И Ц Г Н Л Ъ Ш Б У Ю>;

R=32; k₁=3; k₂=15; b=4.

Пошаговое выполнение алгоритма приводит к получению следующих результатов.

Шаг 1. L_0h=<12, 6, 18, 14, 5, 32, 24, 9, 20, 16, 14, 3, 1, 13, 9, 31>.

Шаг 2. L_1h=<19, 1, 5, 25, 30, 15, 23, 10, 11, 31, 25, 24, 18, 22, 10, 12>.

Шаг 3. T₁=<С О Я Г Б Д И М Ч У Г Ц К П М Х>.

Шаг 4. T₂=<С О Я Г Б Д И М Ч У Г Ц К П М Х>.

При расшифровании сначала устраняется разбиение на блоки. Получается непрерывный шифртекст T₁ длиной K символов. Расшифрование осуществляется путем решения целочисленного уравнения:

k₁h₀₁+k₂=nR+h_1i,

При известных целых величинах k₁, k₂, h_1i и R величина h_0i вычисляется методом перебора n.

Последовательное применение этой процедуры ко всем символам шифртекста приводит к его расшифрованию.

По условиям приведенного примера может быть построена таблица замены, в которой взаимозаменяемые символы располагаются в одном столбце (табл. 1).

 

таблица 1

 

Использование таблицы замены значительно упрощает процесс шифрования. При шифровании символ исходного текста сравнивается с символами строки s_0i таблицы. Если произошло совпадение в i-м столбце, то символ исходного текста заменяется символом из строки s_1i, находящегося в том же столбце i таблицы.

Расшифрование осуществляется аналогичным образом, но вход в таблицу производится по строке s_1i.

Основным недостатком метода прямой замены является наличие одних и тех же статистических характеристик исходного и закрытого текста. Зная, на каком языке написан исходный текст и частотную характеристику употребления символов алфавита этого языка, криптоаналитик путем статистической обработки перехваченных сообщений может установить соответствие между символами обоих алфавитов.

Существенно более стойкими являются методы полиалфавитной замены. Такие методы основаны на использовании нескольких алфавитов для замены символов исходного текста. Формально полиалфавитную замену можно представить следующим образом. При N - алфавитной замене символ s₀₁ из исходного алфавита A₀ заменяется символом s₁₁ из алфавита A₁, s₀₂ заменяется символом s₂₂ из алфавита А₂ и так далее. После замены s_0N символом s_NN из А_N символ s_0(N+1) замещается символом s_1(N+1) из алфавита A₁ и так далее.

Наибольшее распространение получил алгоритм полиалфавитной замены с использованием таблицы (матрицы) Вижинера T_B, которая представляет собой квадратную матрицу [RxR], где R - количество символов в используемом алфавите. В первой строке располагаются символы в алфавитном порядке. Начиная со второй строки, символы записываются со сдвигом влево на одну позицию. Выталкиваемые символы заполняют освобождающиеся позиции справа (циклический сдвиг). Если используется русский алфавит, то матрица Вижинера имеет размерность [32 x 32].

Рис. 2. Матрица Вижинера

 

Шифрование осуществляется с помощью ключа, состоящего из М неповторяющихся символов. Из полной матрицы Вижинера выделяется матрица шифрования Т_ш, размерностью [(М+1), R]. Она включает первую строку и строки, первые элементы которых совпадают с символами ключа. Если в качестве ключа выбрано слово <ЗОНД>, то матрица шифрования содержит пять строк (рис. 3).

 

Рис. 3. Матрица шифрования для ключа <ЗОНД>

 

Алгоритм зашифрования с помощью таблицы Вижинера представляет собой следующую последовательность шагов.

Шаг 1. Выбор ключа К длиной М символов.

Шаг 2. Построение матрицы шифрования Т_ш=(b_ij) размерностью [(М+1), R] для выбранного ключа К.

Шаг 3. Под каждым символом s_0r исходного текста длиной I символов размещается символ ключа k_m (рис. 2.1.2). Ключ повторяется необходимое число раз.

Шаг 4. Символы исходного текста последовательно замещаются символами, выбираемыми из Т_ш по следующему правилу:

1) определяется символ km ключа К, соответствующий замещаемому символу sor;

2) находится строка i в Тi, для которой выполняется условие km=bi1;

3) определяется столбец j, для которого выполняется условие: sor=b1j;

4) символ sor замещается символом bij.

 

Шаг 5. Полученная зашифрованная последовательность разбивается на блоки определенной длины, например, по четыре символа. Последний блок дополняется, при необходимости, служебными символами до полного объема.

Расшифрование осуществляется в следующей последовательности:

Шаг 1. Под шифртекстом записывается последовательность символов ключа по аналогии с шагом 3 алгоритма зашифрования.

Шаг 2. Последовательно выбираются символы s_1r из шифртекста и соответствующие символы ключа K_m. В матрице Т_ш определяется строка i, для которой выполняется условие K_m = b_i1. В строке 1 определяется элемент b_ij = s_1r. В расшифрованный текст на позицию r помещается символ b_1j.

Шаг 3. Расшифрованный текст записывается без разделения на блоки. Убираются служебные символы.

Пример.

Требуется с помощью ключа К = <ЗОНД> зашифровать исходный текст Т = <БЕЗОБЛАЧНОЕ_НЕБО>.

Механизмы зашифрования и расшифрования представлены на рис. 4.

 

Исходный текст	БЕЗОБЛАЧНОЕ_НЕБО
Ключ	ЗОНДЗОНДЗОНДЗОНД
Текст после замены	ИУФТИШНЫФЫТГФУОТ
Шифртекст	ИУФТ ИШНЫ ФЫТГ ФУОТ
Ключ	ЗОНД ЗОНД ЗОНД ЗОНД
Расшифрованный текст	БЕЗО БЛАЧ НОЕ_ НЕБО
Исходный текст	БЕЗОБЛАЧНОЕ_НЕБО

Рис. 4. Пример шифрования с помощью матрицы Вижинера

 

Криптостойкость методов полиалфавитной замены значительно выше методов простой замены, так как одни и те же символы исходной последовательности могут заменяться разными символами. Однако стойкость шифра к статистическим методам криптоанализа зависит от длины ключа.

Для повышения криптостойкости может использоваться модифицированная матрица шифрования. Она представляет собой матрицу размерности [11, R], где R - число символов алфавита. В первой строке располагаются символы в алфавитном порядке. Остальные 10 строк нумеруются от 0 до 9. В этих строках символы располагаются случайным образом.

В качестве ключей используются, например, непериодические бесконечные числа π, е и другие. Очередной n-й символ исходного текста заменяется соответствующим символом из строки матрицы шифрования, номер которой совпадает с n-й цифрой бесконечного числа.