Методы дисконтирования в условиях определенности.
1. Дисконтированный срок окупаемости капитальных вложений.
2. Анализ чувствительности ЧДД к различным факторам.
3. Отбор проектов по критерию ЧДД и по показателю внутренней нормы доходности капитальных вложений.
- 1 –
Дисконтированный срок окупаемости – это такой период времени Тдок в течение которого инвестор накапливает денежные средства для инвестирования равные по своей величине первоначальным капитальным вложениям. Это такой момент времени начиная с которого ЧДД становится положительным. Значения дисконтированного срока окупаемости определяется графическим способом, с помощью графика ЧДД=F(t).
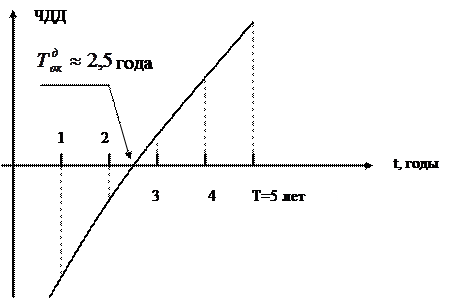
За 2,5 года инвестор вернет первоначальный капитал и получит дивиденды в размере 
годовых.
Чем больше разница между продолжительностью фазы эксплуатации проекта и дисконтированным сроком окупаемости (Т – Тдок), тем величина ЧДД будет больше. Величину Т прогнозируют маркетологи с той или иной точностью.
Тдок – минимальная продолжительность жизненного цикла проекта.
Методика расчета дисконтированного срока окупаемости.
Задаются продолжительностью жизненного цикла проекта t = 1,2,3….Т. Для этих значений рассчитывают ЧДД, наносят на график и определяют Тдок .
Пример:
Определить дисконтированы срок окупаемости капитальных вложений.
К = 2487 тыс.руб. Продолжительность фазы эксплуатации проекта Т =5 лет. Годовые чистые денежные поступления аннуитетные Д = 1000 тыс.руб./год, ставка дисконтирования i =0,1. определить средний срок ликвидности капитальных вложений (простой срок окупаемости) и дисконтированный.
Решение:
Определим средний срок ликвидности капитальных вложений:
Тл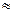 
2,5 года (первый год – 1000, второй год - 1000 и еще за полгода – 5000 тыс. руб.).
Определим дисконтированный:
t = 1 год: 
тыс.руб.
t = 2 года: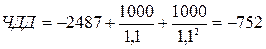 
тыс.руб.
t = 3 года: 
t = 4 года: 
тыс.руб.
Построим график зависимости ЧДД=F(t).
 |
Дисконтированный срок окупаемости всегда больше простого срока окупаемости Тл < Тдок (2,5 < 3), так как инвестор получает проценты из годовых чистых денежных поступлений. Чем величина процентов будет больше, тем разница будет больше.
- 2 –
Цель анализа чувствительности ЧДД к различным факторам – оценка того, насколько значение ЧДД существенно и отлично от нуля, то есть не находится ли значений ЧДД в пределах точности прогнозов.
Чувствительность ЧДД исследуется по отношению к следующим факторам:
1. К изменению величины первоначальных капитальных вложений .
2. К изменению величины годовых чистых денежных поступлений .
3. К изменению величины продолжительности жизненного цикла проекта .
4. К изменению ставки дисконтирования.
Необходимо ввести в рассмотрение ошибку точности прогноза того или иного фактора. Если запас проекта по тому или иному фактору превышает ошибку прогноза, то проект по этому фактору будет надежен.
Пример:
К=300 тыс.руб.; Д1=165 тыс.руб.; Д2=203 тыс.руб.; Д3=247 тыс.руб. Рассчитать ЧДД при ставке дисконтирования i =0,3 и провести анализ чувствительности дохода.
Решение:
тыс.руб.
1) На сколько может быть превышена смета первоначальных капитальных вложений, с тем чтобы проект еще оставался эффективным? Очевидно, что Кmax=359 тыс. руб. Процент превышения сметы первоначальных капитальных вложений
Если строители превышают сметы первоначальных капитальных вложений, например, на 16%, то проект по этому фактору будет надежным, поскольку запас проекта по ЧДД больше процента завышения сметы 19,7% >16%
2) На сколько могут уменьшаться годовые чистые денежные поступления, с тем чтобы проект еще оставался эффективным. Предположим, что годовые чистые денежные поступления в процессе реализации уменьшились на х %, определим то значение х при котором ЧДД превращается в ноль:
х = 17%
Если маркетологи в среднем ошибаются в прогнозировании денежных потоков на 10%, то проект по этому фактору будет устойчивым 17% > 10%.
3) Определим минимальную продолжительность жизненного цикла проекта, то есть дисконтированный срок окупаемости капитальных вложений. Задавая различные значения t, рассчитаем ЧДД и определим, что Тдок =2,5 года. При прогнозе 3 года запас 
Т =0,5 года.
Если маркетологи ошибаются в прогнозировании жизненного цикла проекта не более чем на 10%, то 17% > 10% - проект надежен.
4) Чувствительность проекта к дивидендам или к процентной ставке. Необходимо рассчитать внутреннюю норму доходности данного проекта. Ранее было рассчитано: r =0,43%. Разница 0,43 – 0,3 = 0,13 (13% годовых) эквивалентна 59 тыс. руб. чистого дисконтированного дохода.
Если проект неустойчив по какому-то конкретному фактору, а по остальным устойчив, то данный фактор является «слабым звеном» и его надо укреплять.
- 3 –
Если из двух или многих проектов нужно выбрать лучший, то это можно сделать либо по критерию ЧДД, либо по критерию внутренней нормы доходности капитальных вложений: ЧДД>0, либо i<r.
Очевидная ситуация: капитальные вложения по проекту А больше кап. вложений по проекту В, а годовые чистые денежные поступления по проекту А меньше, чем по проекту В:
КА>КВ,
ДА<ДВ.
Проект А однозначно хуже проекта В.
Чаще встречается следующая ситуация, например КВ>КА, ДВ >ДА. Какой из этих проектов лучше? Для решения этой задачи строят на плоскости два графика зависимости ЧДД от ставки дисконтирования.
Внутренняя норма доходности rA > rB.
Казалось бы, что проект А лучше проекта В, однако это неправильно: все зависит от ставки дисконтирования.
Если i < iкр , то проект В лучше, т.к. у него ЧДД больше.
Если i > iкр , то лучше проект А, т.к. проект В уже убыточен, а проект А еще приносит доход.
Если i = iкр, то эти проекты эквивалентны.
Из графика можно получить дополнительную информацию по проектам А и В:
;
Первая производная от ЧДД по i:
.
Первая производная показывает тангенс угла наклона касательной к кривой ЧДД(i) в данной точке. У долгосрочных проектов (с большей продолжительностью жизненного цикла) тангенс угла наклона кривой к оси i в точке r будет всегда больше. Очевидно, что проект В – долгосрочный. Значит, долгосрочные проекты, как правило, при прочих равных условиях имеют меньшую внутреннюю норму доходности капитала, чем краткосрочные. Проект А – краткосрочный.
Если в данной отрасли стоимость капитала очень высокая (инвесторы требуют больших дивидендов), то будут реализоваться краткосрочные проекты.
Пример.
Два проекта имеют различную величину первоначального капитала. Следует выбрать лучший проект.
| Проект | Капитал, тыс.руб. | Денежные поступления, тыс. руб. |
| А | ||
| В |
Решение:
Рассчитаем внутреннюю норму доходности этих проектов, а затем определим пересечение Фишера.
→ rA=0,2
→ rB=0,18
Из того, что rA> rB вовсе не следует, что проект А лучше проекта В.
Определим критическую ставку дисконта, т.е. пересечение Фишера:
return false">ссылка скрыта
= 
отсюда iкр=0,14.
Построим график.
Если i>0.14 – то лучше проект А, т.к. ЧДД больше.
Если i=0.14 – то проекты эквивалентны.
Если i<0.14 – то лучше проект В, т.к. ЧДД больше.
Другой способ выбора лучшего проекта
Воспользуемся принципом однородной эффективности вложенного капитала (вводится проект с дополнительным объемом капитала; рассчитывают внутреннюю норму доходности дополнительного проекта и делают выводы).
Пример.
КА=10000 тыс. руб.,
ДА=12000 тыс.руб.\год.
Этот проект А следует сравнить с проектом В:
КВ=15000 тыс. руб.,
ДВ=17700 тыс.руб.\год.
Введем в рассмотрение дополнительный проект, который является частью проекта В. У этого проекта чистые денежные поступления ∆ДВ= 5700 тыс. руб., а кап. вложения ∆КВ= 5000 тыс.руб.
Рассчитаем внутреннюю норму доходности дополнительного проекта:
, очевидно, что r=0,14.
Если i>0.14 – то часть В не эффективна, следовательно и весь проект хуже А.
Если i<0.14 – то часть проекта В лучше проекта А, следовательно и весь проект В лучше А.
Вывод тот же, что и в случае, когда определялось пересечение Фишера.