Движение тела в неподвижной жидкости.
Рассмотрим известный опыт Ньютона. Пусть имеются две параллельные пластинки, между которыми находится газ (жидкость).
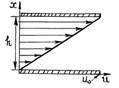 Расстояние между пластинками h. Нижнюю пластинку будем удерживать неподвижно, верхнюю заставим двигаться в одном и том же направлении в своей плоскости с постоянной скоростью u0.
Слой газа, непосредственно прилегающий к верхней пластинке, будет иметь ту же скорость u0, что и пластинка, слой же газа, прилегающий к нижней пластинке, находится в покое. Как показывает опыт, любой промежуточный слой движется со скоростью u, пропорциональной расстоянию x от неподвижной пластинки, т. е. u=ax.
Постоянная a определяется из условия, что при x = h u = u0, т. е. u0 = ah. Откуда a = u0/h. Тогда выражение примет вид u=(u0/h)x.
Таким образом, к верхней пластинке приложена сила F1, лежащая в ее плоскости и имеющая то же направление, что и направление движения пластинки. Так как пластинка движется с постоянной скоростью u0, то на пластинку должна действовать такая же по величине, но противоположно направленная сила F со стороны газа, которую назовем силой вязкого трения.
Из опыта следует, что абсолютная величина силы F1 пропорциональна скорости u0, с которой мы двигаем пластинку, и площади пластины, т. е. Расстояние между пластинками h. Нижнюю пластинку будем удерживать неподвижно, верхнюю заставим двигаться в одном и том же направлении в своей плоскости с постоянной скоростью u0.
Слой газа, непосредственно прилегающий к верхней пластинке, будет иметь ту же скорость u0, что и пластинка, слой же газа, прилегающий к нижней пластинке, находится в покое. Как показывает опыт, любой промежуточный слой движется со скоростью u, пропорциональной расстоянию x от неподвижной пластинки, т. е. u=ax.
Постоянная a определяется из условия, что при x = h u = u0, т. е. u0 = ah. Откуда a = u0/h. Тогда выражение примет вид u=(u0/h)x.
Таким образом, к верхней пластинке приложена сила F1, лежащая в ее плоскости и имеющая то же направление, что и направление движения пластинки. Так как пластинка движется с постоянной скоростью u0, то на пластинку должна действовать такая же по величине, но противоположно направленная сила F со стороны газа, которую назовем силой вязкого трения.
Из опыта следует, что абсолютная величина силы F1 пропорциональна скорости u0, с которой мы двигаем пластинку, и площади пластины, т. е. 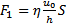 , где – , где –  постоянный коэффициент пропорциональности, который называют коэффициентом вязкого трения. Учитывая, что сила вязкого трения F=-F1 , равенство перепишем в виде постоянный коэффициент пропорциональности, который называют коэффициентом вязкого трения. Учитывая, что сила вязкого трения F=-F1 , равенство перепишем в виде  .
Так как следует, что du/dx=u0/h, то последнее выражение можно представить так: .
Так как следует, что du/dx=u0/h, то последнее выражение можно представить так:
 Это закон внутреннего вязкого трения Ньютона, который утверждает: при стационарном (ламинарном) движении слоев жидкости или газа с различными скоростями между ними возникают касательные силы, пропорциональные градиенту скорости слоев и площади их соприкосновения.
Если в жидкость поместить пластинку и двигать с постоянной скоростью вперед, то при небольшом расстоянии, вторую пластинку нужно удерживать силой, которая равна силе, которую нужно приложить к пластинке, чтобы она двигалась (Сила вязкого трения).
Это закон внутреннего вязкого трения Ньютона, который утверждает: при стационарном (ламинарном) движении слоев жидкости или газа с различными скоростями между ними возникают касательные силы, пропорциональные градиенту скорости слоев и площади их соприкосновения.
Если в жидкость поместить пластинку и двигать с постоянной скоростью вперед, то при небольшом расстоянии, вторую пластинку нужно удерживать силой, которая равна силе, которую нужно приложить к пластинке, чтобы она двигалась (Сила вязкого трения).
|