Беттік керілу
1. Сұйық молекуласына айналысындағы басқа молекулалар тарапынан тартылу күштері әсер етеді. Егер молекула сұйық бетінен молекулалық әсерлесу сферасының радиусынан артық арақашықтықта, демек, сұйық ішіндегі орналасса, онда оған әсер етуші күштер тепе теңдік күйде болады. егер молекула қалыңдығы молекулалақы әсерлесу сферасының радиусына тең болатын шекаралық қабатта болса, онда оған сұйық ішіне қарай бағытталған қорытқы күш әсер етеді. Сондықтан молекуланы сұйық ішінен беттік қабатқа шығару үшін жұмыс атқару керек. Сұйық бетінің ауданын изотермиялық және квазистатикалық бір бірлікке (көлемді сақтап) арттыруға қажетті жұмысты сұйықтың беттік керілуі деп атайды. Изотермиялық жұмыс жүйенің еркін энергиясының кемуіне тең. Сыртқы күштер әсер етпейтін сұйықтың еркін энергиясын мына түрде жазуға болады:
(1)
Мұндағы 
еркін энергияның көлемдік және беттік құраушылары. Егер сұйықтың көлемі өте үлкен болса, онда 
, демек 
. Ал, егер сұйықтың көлемі аз болса, онда 
. Жоғарыда айтылғандарды ескерсек
(2)
мұндағы 
сұйықтың беттік керілуі, 
сұйық бетінің ауданы. Сонымен беттік керілуді сұйық аудан бірлігіндегі беттің еркін энергиясы ретінде қарастыруға болады.
2.Тік бұрышты сымнан жасалған каркас алайық. Каркастың СД бөлігі АС және ВД бағыттары бойынша еркін сырғи алсын.АВДС ауданына жұқа сабын қабыршақ тартайық. Бұл қабыршақ екі жақты. Осы екі қабыршақтың ортасында сұйық бар. Тәжірибелерден қабырщақтың қысқаруға ұмтылатынын көруге болады. сондықтан СД жоғары қарай қозғалады. СД-ны орнында ұстап тұру үшін белгілі күшпен әсер ету керек, мысалы жүк ілу керек. Қабықша екеу болғандықтан бұл күшті 2Ғ деп белгілейміз. Егер температураны тұрақты етіп ұстап Ғ күшін өте аз шамаға көбейтсек, онда СД төмен қарай 
жол жүреді және қабыршақ үстінен 
жұмыс атқарады. Бұл кезде қабыршақ ауданы 
шамаға артады. Мұндағы l- СД ның ұзындығы; 
әрбір қабықшаның ауданының өсімшесі. 
. Осы екі өрнекті теңестіріп,
(3)
екенін анықтаймыз.
(4)
Бұдан қабықшаның керілген күйде екенін көруге болады.
Сұйықтың беттік керілуін анықтағанда оның қандай ортамен шектесетінін білу қажет. Беттік керілу температура артқанда кемиді
(5)
§48Шектік бұрыштар. Жұғу және жұқпау
1. 1,2,3 сұйық орталар бір бірімен жұптасып шекаралас болсын. Бұл сұйықтар сурет бетіне перпендикуляр бағытталған. О түзуінің бойымен қиылысатын беттер арқылы шектессін. Осы сұйықтар бір бірімен тепе теңдікте болуы үшін барлық күштердің қосындысы нөлге тең болуы керек. Қимасы S болатын цилиндр ішінде тепе теңдік болуы үшін беттік керілу күштерінің ( 
) S бетіне түсірілетін гидростатикалық қысым күші және сұйықтың ауырлық күші қосындылары нөлге тең болады. соңғы екі күш бір біріне қарсы бағытталған және шамалас, сондықтан тепе теңдік шартын былай жазамыз:
(6)
2. Лаплас формуласын радиусы а болатын цилиндр капилляр ішіндегі сұйық бағанының көтерілу биіктігін есептеуге қолданайық. Сұйық деңгейінің а шамаға өзгергендегі қысым өзгерісін ескермейік. Бұл жуықтауда меншіктің барлық нүктелерінде 
қысым айырымы бірдей болады. Сондай ақ орташа қисықтық 
ге ұмтылар, демек, 
. Қисықтың радиусы
мұндағы 
шектік бұрыш.
Мұнда 
атмосфералық қысым, ал 
сұйықтың меншікті деңгейіндегі қысымы. Бұл қысымдар айырымы былай анықталады:
Мұндағы һ- сұйық деңгейі,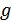 
- сұйық тығыздығы. Бұл формуланы (4) формуламен салыстырсақ
§49. Сұйықтың майысқан бетінің екі жағындағы қысымдар айырымы. Лаплас формуласы
1.Егер сұйық беті қисық болса, онда тепе теңдікте оның екі жағындағы қысым әр түрлі болады. Бұл құбылыс беттік керілу күштеріне байланысты. Біз қимасы дөңгелек,цилиндр пішімді ыдыстағы сұйықты қарастырайық. Сұйық бетінде өте аз АВ бөлігін алайық, АОВ бұрышы φ болсын. Осы бөліктің жақтарына жанама бойымен b күштері әсер етеді. Мұндағы в цилиндр ұзындығы. Осы екі күштердің тең әсерлісі СО бағытымен бағытталған және былай анықталады
немесе 
, себебі φ бұрышы шексіз аз. 
;
а-АВ доғасының ұзындығы, R - цилиндр радиусы.
(1)
-
Осы күшті S- ауданға бөлсек, онда сұйықтың ішіндегі және сыртындағы қысымдардың аыйрымын аламыз.
(2)
2. Енді осы формуланы сұйық екі жақты қисық бетпен шектесетін жағдай үшін шығарайық. Сұйық бетінен А.В,С,Д өте аз тікбұрышты төртбұрыш төбелері болатын нүктелерін алайық. А және В, В және С нүктелері арқылы сұйық бетіне перпендикуляр жазықтықтар жүргізейік. Суретте АД және ВС нүктелері арқылы жүргізілген жазықтықтар көрсетілген. Соның нәтижесінде өте аз қисық тік ұрышты төртбұрыш АВСД аламыз. Оның жақтары шеңберлердің өте аз доғалары сияқты. R1АВ-доғасының радиусы. ДС доғасының қисықтық радиусы R1деп өте аз шамаға айрықшаланады. АД және ВС жақтарына жанама беттік керілу күштері әсер етеді. Бұл күштердің тең әсерлісі сұйық бетіне нормаль бағытталған. (1) формулаға сәйкес 
, мұндағы S- ABCD тікбұрышының ауданы. AB және CD жақтарына әсер ететін жанама беттік керілу күштерінің де тең әсерлесі бұлай анықталады: 
, мұндағы 
AD доғасының қисықтық радиусы. Сонымен тікбұрышының шеттеріне әсер ететін барлық беттік керілу күштерінің тең әсерлісі бұлай анықталады
Бұл күшті S–ауданға бөліп, іздеп отырған қысымдар айырылып аламыз:
(3)
Бұл формула (3) Лаплас формуласы деп аталады. 
өзара перпендикуляр беттердің қисықтық радиустары. Егер сұйық беті дөңес болса, онда қисықтық радиусы оң, ойыс болса – теріс деп есептеледі. 
қосындысы беттің орташа қисықтығы деп аталады. Орташа қисықтың өзара перпендикуляр беттерді таңдауға тәуелді емес. Бұл тәуелсіздік Эйлер теоремасы деп аталады.
3.Егер сұйық беті сфералық болса, онда болып (3) формула бұлай өзгереді:
(4)
Сабын көпіршігі үшін көпіршіктің ішіндегі және сыртындағы қысымдар айырмасы (4) формуладағыға қарағанда 2 есе көп болады:
(5)
Мұның себебі көпіршіктік қабыршағының екі беті бар.
2.Үш ортаның бір бірімен шектесуі мысалы ретінде бір сұйық бетіндегі екінші сұйық тамшысын қарастырып көруге болады. тамшысының формасы суретте көрсетілгендей болады. бұл жағдайда тепе–теңдіктің векторлық шарты екі скаляр теңдеу түрінде жазылады.
(7)
Бұл теңдеулерден
, 
(8)
Осы формулалармен 
бұрыштары анықталады. Сұйықтардың тепе – теңдігі 
шарты орындалғанда орындалады. Бұл жағдайда тамшы формуласы суреттегідей болады. Егер 
болса, онда тепе – теңдік бұзылып тамшы 3-сұйықтың бетіне жайылып жұқа қабықша құрайды. Мұндай жағдайда 3-сұйық 2-сұйыққа толық жұғысады деп айтамыз.
3. Қатты дене бетіндегі сұйық тамшысы да осылай болады. Негізгі айырмашылығы қатты дене деформацияланбайды. Беттік керілу күштерінің тең әсерлі күші нормаль қысым күшімен немесе сұйық пен қатты дене шекарасындағы керілу күшімен теңеседі. Сондықтан
өрнегінің орнына оның тек жанама бойымен бағытталған қорытқы күштің нөльге тең болуын талап ету керек. Қарастырып отырған жағдайда 
сондықтан 
бұрышын анықтау үшін бір теңдеу жеткілікті 
(9)
мұндағы α-бұрышы шеттік бұрыш деп аталады.
Егер 
, демек болса онда (9) өрнек қанағаттандырылмайды. Сұйық тамшысы (2)тепе-теңдікке келмей қатты дене бетіне жұқа қабықша болып жайылып кетеді. Бұл жағдайда сұйық қатты дене бетіне «толық жұғысты» деп айтамыз. Басқаша жағдайда 
, демек, 
болғанда да (9) өрнекті қанағаттандыратын αбұрышы жоқ. Сұйық шар тәріздес тамшы болып жиырылады, тек ауырлық күші әсерінен кішкене қысылады. Бұл жағдайда сұйық қатты дене бетіне «толық жұқпайды» деп айтамыз. Көбінесе, αбұрышы 
аралығында болса, шамалы жұғысу, ал 
болса, шамалы жұғыспау орын алады.
§50. Фазалар және фазалық түрленулер
1. Фаза деп жүйенің басқа бөліктерімен шекаралармен бөлінген, заттың физикалық біртекті макроскопиялық бөлігін айтамыз. Мысалы, жабық ыдыс ішінде судың белгілі мөлшері және оның үйінде ауа мен су буының қоспасы болсын. Мұндай жүйені екі фазалы жүйе деп айтамыз. Бұл жүйе екі фазадан тұрады: сұйық (су) және газ тәріздес (ауа мен су буының қоспасы). Егер ауа болмаса, онда да жүйеде екі фаза болады (су мен су буы). Осы суға бір кесек мұз салып қойсақ, онда жүйе үш фазалық жүйеге айналады. Жүйеде үш фаза – қатты (мұз), сұйық (су) және газ тәріздес (су буы мен ауа). Егер суға спирт қоссақ, онда фазалар саны өзгермейді, себебі спирт пен су бір бірімен жақсы араласады. Егер суға сынап қоссақ, онда жүйеде екі сұйық фаза болады, себебі, су мен сынап араласпайды. Газ тәріздес фаза бәрібір біреу болып қалады. Жүйеде бірнеше қатты және сұйық фазалар болуы мүмкін, ал газ тәріздес фаза тек қана біреу болады. Себебі, газдардың барлығы бір бірімен жақсы араласады.
2. Фазаларды зерттегенде екі немесе бірнеше фазадан тұратын жүйе қандай жағдайда тепе-теңдікте болатынын анықтау негізгі мәселе. Тепе-теңдік механикалық және жылулық болады. жылулық тепе-теңдік болуы үшін жүйеге енетін барлық фазалар бірдей температурада болуы керек. Механикалық тепе-теңдік болуы үшін бір бірімен шектесетін фазаладрдың шекараларының екі жағындағы қысымдар тең болуы керек.
Қысымдар мен температуралардың тең болуы жүйенің тепе-теңдікте болуын толық қамтамасыз етпейді. Себебі, шекаралас фазалар бір біріне өтуі мүмкін. Мұндай түрленулерді фазалық түрленулер деп атаймыз. Фазалық түрленулер екзінде бір фаза көбейіп, екіншісі азайып тіптен жоқ болып кетуі мүмкін. Сондықтан тепе-теңдіктің тағы бір шарты – ол жүйедегі фазалардың массаларының тұрақтылығы. Демек, тепе-теңдіктің тағы бір шарты фазалық түрленуге қатысты тепе-теңдік. Осы шарт фазалардың тепе-теңдігінің негізгісі болып табылады.
3.Фазалық түрленулердің мысалы ретінде заттың агрегаттық күйінің өзгеруін алуға болады. Агрегаттық күйлер деп қатты, сұйық және газ тәріздес күйлерді айтамыз. Қатты және сұйық күйлер конденсирленген күй деп аталады. Булану деп заттың конденсирленген күйден газ тәріздес күйге айналуын айтамыз. Кері процесті конденсация процесі деп аталады. Қатты күйден бірден газ күйіне өтуді сублимация деп атайды. Қатты күйден сұйық күйге өту балқу деп аталады. Ал, сұйық күйден қатты күйге өту қатаю немесе кристалдану деп аталады. Заттың қатты күйі әр түрлі кристалдық модификацияларда болуы мүмкін. Бұл құбылыс полиморфизм деп аталады. Мысалы, қатты көміртегі графит немесе алмаз түрінде болады. олардың кристалдық құрылымдары әр түрлі. Қатты темір 4 түрде кездеседі (α,β,γ,δ темір). Сол сияқты кейбір сұйықтар да әр түрлі модификацияда болады: (сұйық гелий І, ІІ). Температура мен қысым өзгергенде модификациялар да өзгереді. Мұны полиморфтық түрленулер деп атаймыз.
4.Фазалық түрленудің тағы бір қарапайым мысалын қарастырайық – булану және конденсация. Ыдыс ішінде сұйықтың массасы және оның бетінде буы болсын. Ыдыс көлемі тұрақты және температурада өзгермесін. Зат молекулалары үнемі қозғалып сұйық пен бу шекарасын кесіп өтетін болсын. Осы екі фаза арасында үнемі молекулалардың ауысы орын алады. Егер сұйықтан буға өтетін молекулалар саны будан сұйыққа өтетін молекулалар санынан көп болса, онда сұйық көлемі азаяды, демек булану процесі жүреді. Бұл жағдайда су бетіндегі буды қанықпаған немесе аса қызған деп атайды. Егер керісінше болса, онда бу аса қаныққан бу деп аталады.
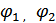меншікті термодинамикалық потенциалдар.
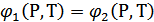фазалардың тепе теңдік шарты.
Термодинамикалық потенциал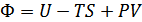 
- меншікті көлемдер
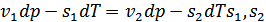- меншікті энтропия
; 
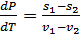рпрпарп
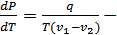Клапейрон-Клаузиус теңдігі
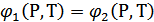
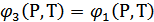
А – үштік нүкте