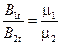Граничные условия для электрического и магнитного полей
Граничные условия для электрического и магнитного полей определяют поведение нормальных и тангенциальных составляющих напряженностей и индукций электрического и магнитного полей на границе раздела двух сред с различными характеристиками. В простейшем случае эти среды будем считать изотропными, т.е. диэлектрические и магнитные проницаемости будут определены как скалярные величины
; 
.
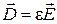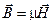Для определения поведения нормальных к поверхности составляющих путем интегрирования уравнений Максвелла III и IV выберем замкнутую поверхность в виде бесконечно малого цилиндра высотой h и с площадью основания DS, предполагая в дальнейшем устремление каждого из этих параметров к нулю (рис. 4).
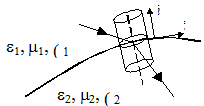
Рисунок 4 – замкнутая поверхность в виде бесконечно малого цилиндра
Интегрируя уравнение Максвелла III
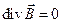
по объему и применяя теорему Остроградского-Гаусса, получим
.
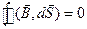Вычисляя потоки через «дно», «крышку» и «боковую поверхность», получим
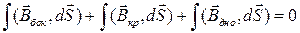
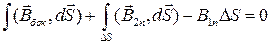
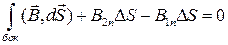
Устремим высоту цилиндра к нулю:
B1n = B2n (1.13)
– первое граничное уравнение.
Используя 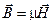, имеем:
. (1.14)
Интегрируя уравнение IV Максвелла
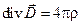
по объему и применяя теорему Остроградского-Гаусса, получим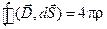 
. В итоге, как и в предыдущем случае, получаем
D2nDS – D1nDS = 4psDS Þ D2n – D1n = 4ps. (1.15)
– скачок на заряженной поверхности, вследствие наличия поверхностной плотности электрических зарядов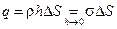 
. С учетом 
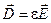, имеем:
e2E2n – e1E 1n = 4ps (1.16)
Если поверхностных зарядов нет, то нормальные составляющие индукции электрического поля непрерывны, а – напряженности изменяются по закону
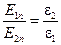(1.17)
Для определения поведения тангенциальных составляющих поле выберем замкнутый контур, представленный на рис. 4.
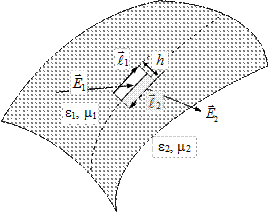
Рисунок 5 – бесконечно малый контур
Интегрируя уравнение II Максвелла
по поверхности, натянутой на контур, и применяя к левой части теорему Стокса, получим
.
Вычисляя по отдельности циркуляции вдоль каждой из сторон контура и устремляя h®0, получим при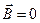 
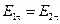
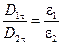. (1.17)
Интегрируя уравнение I Максвелла
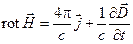
по поверхности, натянутой на контур, и применяя к левой части теорему Стокса, получим
, 
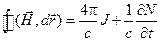
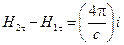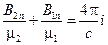(1.18)
где i – линейная плотность поверхностных токов.
Если отсутствуют поверхностные токи i = 0, то 