Аппроксимация экспериментальных данных методом среднеарифметического

Метод среднеарифметического - заключается в том, что неизвестные коэффициенты степенного полинома определяются таким образом, что сумма отклонений точек расположенных с одной стороны графика равна сумме отклонений точек расположенных с другой стороны (арифметическая сумма всех отклонений равна нулю).

Отклонение еi это разница между значением функции по обобщающему полиному у=ао+а₁х+а ₂ х²+а₃ х³... а _m х^m и экспериментальным результатом у, для одного и того же значения х,.

еi =ао+а₁х+а ₂ х²+а ₃ х³... а_m х^m-y (15)

(16)

Условием метода является следующее выражение

Составляется система из п уравнений, где п - число экспериментальных точек.

 

 

Имеющуюся систему из п уравнений разбивают на подгруппы, количество подгрупп равно количеству неизвестных коэффициентов степенного полинома (т+1). Полученная таким образом система из (т+1) уравнений решается совместно, и определяются неизвестные коэффициенты.

 

 

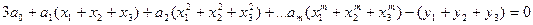
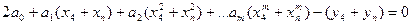
Недостатком метода является то, что его нельзя использовать при ограниченном количестве экспериментальных точек п.

Метод среднеарифметического может быть применен для различных кривых после их выравнивания.

 

Пример: Пусть, имеются результаты восьми замеров:

 

X
Y	57,3	41,9	31,0	22,7	16,6	12,2	8,9	6,5

Вид кривой в прямоугольных координатах дает возможность
применить формулу y = ae^-bx (рисунок 1б)

 

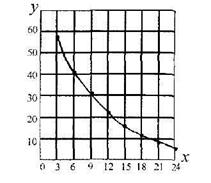
Рисунок 3 -Экспериментальный график в прямоугольных координатах

 

Произведем выравнивание путем замены переменных Y=lgy, X=lge^x =0,434x. Тогда Y=lga-b Ige^x и Y=A-bX, где A=lga. Так как неизвестно два коэффициента, то все измерения делятся на две группы по четыре измерения. В результате имеем две системы

 

4A-0,434*30*B-6,2300=0 4A-0,434*78*B-4,0688=0

 

Решение системы из двух уравнений дает: A=1,8952; a=10^A =78,56; b=0,1037.

Окончательная эмпирическая формула будет иметь вид

у=78,56e^-0,1037х.