Выпуклые множества точек

Определение 1. Множество точек плоскости или трехмерного пространства называется выпуклым, если любые две точки этого множества можно соединить отрезком прямой, полностью лежащим в данном множестве (см. рис.6).

Рисунок 6 – Изображение множеств

Теорема 1. Пересечение конечного числа выпуклых множеств является выпуклым множеством.

Следствие. Пересечение конечного числа выпуклых множеств - выпуклое множество.

Определение 2. Точка множества называется внутренней, если существует сколь угодно малая ее окрестность, содержащая только точки данного множества.

Определение 3. Точка множества называется граничной, если любая ее окрестность содержит как точки, принадлежащие данному множеству, так и не принадлежащие ему (см. рис. 7).

Определение 4. Граничная точка выпуклого множества называется угловой, если через нее можно провести отрезок, все точки которого не принадлежат данному множеству (см. рис. 7).

Различные по форме множества могут иметь конечное или бесконечное количество угловых точек.

Рисунок 7 – Изображение точек множества

Пример 1. Определить угловые точки множества, заданного условиями .

Решение. Уравнение имеет бесчисленное множество решений – множество точек, лежащих на прямой. А условие определяет точки этой прямой, лежащие только в. первой четверти координатной плоскости (рис. 8).

Множество точек отрезка АВ представляет собой выпуклое множество допустимых решений с двумя угловыми точками А(0;6)и В(4;0).

Рисунок 8 – решение примера 1

Пример 2. Определить угловые точки множества: , при .

Решение. Множество допустимых решений – луч АС.

Здесь лишь одна угловая точка A (3,0) соответствует единственному допустимому базисному решению (см. рис. 9).

Рисунок 9 – решение примера 2

Как правило, система ограничений в задачах математического программирования представлена в виде системы неравенств, решение каждого из которых занимает определенную часть плоскости (пространства).

Теорема 2. Решением неравенства 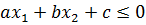или является одна из полуплоскостей, на которые прямая делит всю координатную плоскость.

Пример 3. Построить множество точек, удовлетворяющих неравенству

Решение. Строим прямую (рис. 10). Она разбила всю плоскость на две полуплоскости, одна из которых и является решением неравенства. Для проверки выберем точку О (0; 0) и ее координаты подставим в исходное неравенство. Получим истинное неравенство . Следовательно, полуплоскость, содержащая начало координат, и является решением.

Рисунок 10 – решение примера 3

Пример 4. Построить множество точек, удовлетворяющих неравенству .

Решение. Строим прямую (рис. 11).

Рисунок 11 – решение примера 4

Прямая разделила всю плоскость на две полуплоскости, одна из которых и является решением неравенства. Для проверки выберем, например, точку А (4; 1) и ее координаты подставим в исходное неравенство. Получим ложное неравенство . То есть полуплоскость, содержащая точку А (4; 1), не является решением. Следовательно, решением является другая полуплоскость, не содержащая этой точки.

Замечание. Для того чтобы найти множество точек, удовлетворяющих системе линейных неравенств, необходимо решить каждое из неравенств и затем найти пересечение этих решений.

Пример 5. Построить множество точек, удовлетворяющих системе неравенств:

Строим полуплоскости, соответствующие каждому из неравенств (1)-(6) (рис. 12). Пересечением их решений является многоугольник АFЕDСВ. Угловые точки здесь - вершины многоугольника.