Алгоритм определения ошибки

Пусть имеем n-элементные комбинации (n = k + r) тогда:

1. Получаем остаток от деления Е(х) соответствующего ошибке в старшем разряде, на образующей поленом P_r(x)

2. Делим полученный полином Н(х) на P_r(x) и получаем текущий остаток R(x).

3. Сравниваем R₀(x) и R(x).

- если они равны, то ошибка произошла в старшем разряде.

- если "нет", то увеличиваем степень принятого полинома на Х и снова проводим деления

4. Опять сравниваем полученный остаток с R₀(x)

- если они равны, то ошибки во втором разряде.

- если нет, то умножаем Н(х)х² и повторяем эти операции до тех пор, пока R(X) не будет равен R₀(x).

Ошибка будет в разряде соответствующем числу на которое повышена степень Н(х) плюс один.

Выбор образующего полинома

В теории циклических кодов показано, что образующий полином представляет собой произведение так называемых минимальных многочленов m_i(x), являющихся простыми сомножителями (то есть делящимся без остатка лишь на себя и на 1) бинома xⁿ+ 1:

P(x)=m₁(x)* m₃(x)…m_j(x), (7.2)

где j = d₀ – 2 =( 2t_u.ош+1) – 2 = 2 t_и.ош – 1.

Существуют специальные таблицы минимальных многочленов, одна из которых приведена ниже. Кроме образующего полинома необходимо найти и количество проверочных разрядов r. Оно определяется из следующего свойства циклических кодов: для любых значений l и t_и.ош существует циклический код длины n =2^l – 1, исправляющий все ошибки кратности t_и.ош и менее, и содержащий не более проверочных элементов.

Так как , то откуда .

Очевидно, что для уменьшения времени передачи кодовых комбинаций, r следует выбирать как можно меньше.

После определения количества проверочных разрядов r, вычисления образующего полинома удобно осуществить, пользуясь таблицей минимальных многочленов, представленной в следующем виде:

Таблица 7.1 - Выбор образующего полинома

J=2tи.ош -1	Вид минимальных многочленов для
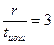
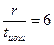
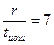
	x2+x+1	x3+x+1	x4+x+1	x5+x+1	x6+x+1	x7+x+1
	-	-	x4+x3+x2+x+1	x5+x4+x3+x2+1	x6+x4+x2+x+1	x7+x3+x2+x+1
	-	-	-	x5+x4+x2+x+1	x6+x5+x2+x+1	x7+x4+x3+x2+1
	-	-	-	-	x6+x3+1	х7+x6+x5+x4+x2+x+1

Определяя образующий полином, нужно из столбца для соответствующего соотношения выписать все многочлены, начиная с верхней строки до нижней с номером j=2t_и.ош–1 включительно. После этого следует перемножить выбранные минимальные многочлены в соответствии с (7.2).