Технические средства реализации информационных процессов.
При рассмотрении технических средств реализации информационных процессов целесообразно выделить следующие аспекты:
Во-первых, представление информации в ЭВМ;
Во-вторых, логические основы построения персонального компьютера;
В-третьих, архитектуру компьютера;
В-четвертых, компьютерные сети.
Представление информации в вычислительных машинах осуществляется с использованием позиционных систем счисления. Под системой счисления понимается способ записи чисел с помощью заданного набора специальных знаков (цифр).
Позиция цифры в числе, записанном с использованием позиционной системы счисления, представляет собой степень, в которую должно быть возведено основание системы счисления, при умножении на данную цифру.
Количество цифр, используемых для записи числа, определяет название системы счисления. В десятичной системе счисления имеется десять цифр (0, 1, 2, … 9). В двоичной системе счисления две цифры (0, 1). В шестнадцатеричной системе счисления используется 16 цифр: (0,1, 2, 3, … 9, A, B,C,D,E,F).
Перевод чисел из любой системы счисления в десятичную систему счисления обеспечивается перемножением цифр числа на основание системы счисления в соответствующей степени:
Примеры:
1) Перевод числа 11011 из двоичной системы счисления в десятичную систему счисления
4 3 2 1 0 4 3 2 1 0
11011 = 1*2 + 1*2 + 0*2 + 1*2 + 1*2 = 16 + 8 + 2 + 1 = 27
2) Перевод числа 51 из восьмеричной системы счисления в десятичную систему счисления
1 0 1 0
51 = 5*8 +1*8 = 40 + 1 =41
Перевод из десятичной системы счисления в другие системы счисления целых чисел обеспечивается делением переводимого числа на основание системы счисления и записью остатков, полученных от деления в обратном порядке.
Пример. Перевод числа 25 из десятичной системы счисления в двоичную систему счисления
25∟2
24 12∟2
 12 6∟2
12 6∟2

 6 3 ∟2
6 3 ∟2
 2
2  Результат: 11001
Результат: 11001
Для обработки в компьютере информация, как правило, кодируется в двоичной системе счисления. В вычислительных машинах применяются две формы представления двоичных чисел:
Во-первых, с фиксированной запятой;
Во-вторых, с использованием нормальной формы.
Нормальной формой представления числа называется число, записанное в виде
A=  m*
m* 
,где
m- мантисса числа;
p- основание системы счисления;
n- порядок числа.
Например, число 21.3410 может быть представлено в следующих видах:
21.34
2134* 
2.134*10
0.2134* 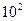
Как правило, при выдаче информации с использованием нормальной формы, используется специальный символ «Е», который определяет порядок числа для десятичной системы счисления.
Например: число “-678.9876” , при выдаче на экран в нормальной форме будет представлено в следующем виде “-6.7898760000E+02”.
Для программирования и анализа вычислительных схем используется математический аппарат алгебры логики. Алгебра логика оперирует с логическими высказываниями. При логической обработке информации используется такое понятие как высказывание.
Под высказыванием понимается любое замечание, сообщение или утверждение об объективно существующем мире. Высказывание может совпадать или не совпадать с действительностью, о которой оно что-то утверждает. Высказывание может быть оценено как истинное (1), или ложное (0). Истина (TRUE) и ложь (FALSE) являются логическими значениями высказываний. Пример высказывания: "На улице идет дождь".
Различают два вида высказываний:
Во-первых, простые высказывания;
Во-вторых, сложные высказывания.
Простые высказывания представляют собой неделимые на части логические объекты. Из простых высказываний можно составить сложные высказывания.
Сложное высказывание состоит из двух и более простых высказываний, соединенных с помощью логических операций. Логическое значение сложного высказывания определяется логическими значениями составляющих его простых высказываний.
В алгебре логике используются такие операции как инверсия, конъюнкция, дизъюнкция.
Операция «инверсия» (логическое отрицание, NOT) преобразует значение «истинно» (1) в значение «ложно» (0), а значение «ложно» в значение «истинно».
Операция конъюнкция (логическое умножение, AND) формирует новое логическое высказывание из двух логических высказываний. Результатное высказывание «истинно» лишь тогда, когда истинны оба входящие в него высказывания.
Операция дизъюнкция (логическое сложение, OR) формирует новое логическое высказывание из двух логических высказываний. Если хотя бы одно из исходных высказываний «истинно», то и результатное высказывание «истинно».
Пример.
Логическое высказывание “ (2=2) And (3>=4) “ будет являться ложным, т.е. будет иметь значение “False”.
Архитектура компьютера, как правило, определяется структурой компьютера и функциональными возможностями машины. В структуре компьютера, прежде всего, выделяют, микропроцессор, основную память и внешнюю память.
Под компьютерной сетью понимается совокупность компьютеров и терминалов, соединенных с помощью каналов связи в единую систему. Компьютерные сети позволяют перейти к распределенной обработке данных. Под распределенной обработкой данных понимается обработка данных, выполняемая на независимых, но связанных между собой компьютерах.