Логический вывод
- это процесс получения некоторого предложения Fn+1 ,исходя из множества предложений S1 путем применения одного или нескольких правил вывода.
Логический вывод -> Если A,то B.
Если известно, что A- истинно, то можно заключить, что B- истинно. Однако, если A-не истинно, то нельзя сделать никакого вывода о B.Утверждение “Если A,то B” будет правильно независимо от того, истинно В или ложно.
Единственный способ показать, что само утверждение о выводимости – ложно- это предъявить ситуацию, в которой известно, что В – ложно, хотя A –истинно.
Цель вывода: показать справедливость отношения
S1|-- Fn+1. В ЛП используется метод резолюции( одно правило вывода)Каждое применение правила называется шагом вывода. Будем применять метод резолюции (правило вывода) только к предложениям трех типов:
Отрицание :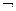 
(A1,….,An)
Факт: А
Правило: A:- B1,….,Bm
(импликация)
где A1,….,An и B1,…..,Bm -произвольные предикаты.
Каждое предложение в логике предикатов первого порядка преобразуется в множество дизъюнктов (то есть объединение множеств). Предложения, являющиеся отрицаниями, фактами и правилами, образуют подкласс класса всех дизъюнктов и называются хорновскими дизъюнктами.
Введем наиболее простую форму резолюции
Пусть имеем:
1случай отрицание S1: 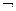A
импликация S2:A:-B
Здесь предикат А из S1 совпадает с заголовком A из S2
В результате первого шага резолютивного вывода получаем из S1 и S2 (родительские предложения) новое предложение s:
s:- 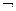B -резольвента, которая получилась в результате применения резолюции к S1 и S2.
Допуская, что не А и А, если В, выводим не В{modus tollens}.
2cлучай: отрицание S1: 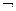A
факт S2:A
Применяя к этим родительским предложениям правило резолюции, выводим в качестве резольвенты пустое отрицание (противоречие):
S: противоречие
Допуская, что не А и А , выводим противоречие
В ЛП вопрос, задаваемый системе, представляется в виде отрицания, и система должна опровергнуть это отрицание при помощи других предложений. Опровержение отрицания происходит путем демонстрации того, что его допущение ведет к противоречию (в математике – доказательство от противного). Резолюция, порождающая последовательность отрицаний, называется резолюцией сверху вниз.
1 шаг – формулировка задачи
2 шаг – запрос (цель)
3 шаг – выполняет ПК, который пытается решить поставленную задачу, строя доказательство от противного.
В теории резолюции есть важный результат:
Из S1 логически следует Fn+1 тогда и только тогда, когда из S1 и 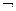F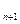 
можно вывести противоречие.
Вывод: построение логического вывода пустого отрицания при помощи правила резолюции означает, что из множества допущений S1 логически следует заключение F 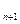.Это заключение прямо отвечает на запрос, поставленный исходным отрицанием F 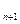и поэтому всегда является утверждением о решении задачи: так как исходное отрицание цели было опровергнуто, то цель – успешна.
Используя метод резолюции совместно с методом унификации можно выводить из имеющихся дизъюнктов все новые дизъюнкты – следствия.
Комбинация методов называется приведением к противоречию. Резолюция позволяет объединить две формулы, удалив из одной А, а из другой 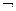А.