Условная энтропия.

Рассматривая формулу Шеннона (3.3) для вычисления энтропии случайной величины и количества информации, мы предполагали, что информация о случайной величине (X) поступает непосредственно к наблюдателю. Однако, как правило, мы получаем информацию не о той случайной величине (X), которая нас интересует, а о некоторой другой (Y), которая связана с X стохастическим образом. Такая связь случайных величин отличается от функциональной связи, при которой каждому значению одной величины соответствует единственное, вполне определённое значение другой величины. Стохастическая (вероятностная) связь двух случайных величин X и Y означает, что изменение одной из них влияет на значение другой, но таким образом, что зная значение X нельзя точно указать значение, которое примет величина Y. Можно лишь указать тенденцию изменения величины Y.

Пусть B – случайное событие; p(B) – вероятность его наступления; обозначим через X случайную величину, которая принимает N различных значений {x₁, x₂, … x_N}, а через A_k событие, состоящее в том, что случайная величина X примет значение x_k:

A_k = { X = x_k}, k=1,2, …N ;

Вероятность события A_k обозначим через p(A_k). Вероятность наступления некоторых событий может меняться в зависимости от того, наступило или нет некоторое другое событие. Вероятность p_B(A_k) события A_k, вычисленная в предположении, что наступило событие B, называется условной вероятностью события A_k , при этом:

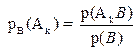(4.1)

События А_k и B называются независимыми, если вероятность наступления события А_k не зависит от того, наступило или нет событие B. Это означает, что условная вероятность события p_B(A_k) равна «обычной» вероятности p(A_k).

Определение. Условной энтропией случайной величины X при условии B называется величина

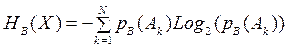(4.2)

Отличие от формулы Шеннона (3.3) заключается в том, что вместо вероятностей p(A_k) используются условные вероятности p_B(A_k).

Пусть теперь Y – другая случайная величина, принимающая значения {y₁, y₂, … y_M}. Обозначим через B_j событие, состоящее в том, что случайная величина Y примет значение y_j:

B_j = { Y = y_j}, j=1, 2,… M.

Вероятность события B_j обозначим через p(B_j).

Определение. Условной энтропией случайной величины X при заданном значении случайной величины Y называется величина H_Y(X)

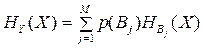(4.3)

Выполним преобразование формулы (4.3):

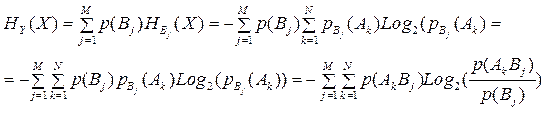
Формула (4.3) принимает вид:

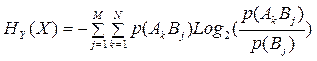(4.4)

Вычислим количество информации о случайной величине X, полученное при наблюдении за случайной величиной Y. Это количество информации I(X,Y) равно убыли энтропии случайной величины X при наблюдении за случайной величиной Y:

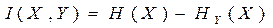(4.5)

Подставим в (15) выражения для H(X) и H_Y(X):

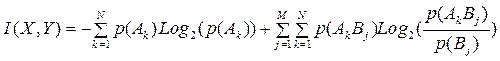
Заменим в первой сумме p(A_k)=p(A_kB₁)+ p(A_kB₂)+ p(A_kB₃)…+ p(A_kB_M). Это равенство действительно имеет место, т.к. события A_kB₁, A_kB₂, … A_kB_M – попарно несовместные, при этом одно из них наступит, если наступит A_k . Наоборот, если наступит одно из B_j , то наступит и A_k . Продолжая преобразования, получим:

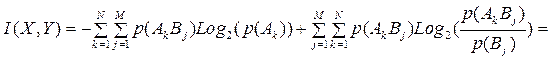
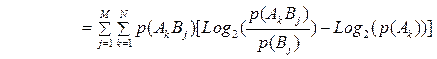
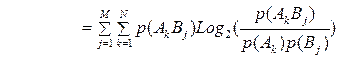
Итак, мы получили формулу для вычисления количества информации о случайной величине X при наблюдении за другой случайной величиной Y:

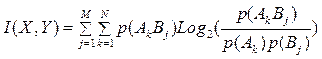(4.6)

Если случайные величины ( или события) независимы, то для них выполняется соотношение p(A_kB_j) = p(A_k)p(B_j) – вероятность совместного наступления двух событий равна произведению вероятностей этих событий.

Относительно величины I(X,Y) справедливы следующие утверждения.

Для независимых случайных величин получим

I(X,Y) = 0.

Это означает, что наблюдение за случайной величиной Y не даст никакого преимущества в получении информации о случайной величине Х.

В других случаях I(X,Y) >0, при этом выполняется неравенство:

I(X,Y) £ H(X).

Равенство достигается в случае наличия функциональной связи Y=F(X). В этом случае наблюдение за Y даёт полную информацию о X. Если Y=X, то I(X,X) = H(X).

Величина I(X,Y) симметрична: I(X,Y) = I(Y,X). Это означает, что наблюдение случайной величины Y даёт такое же количество информации о случайной величине Х, какое наблюдение случайной величины Х даёт относительно случайной величины Y. Если мы рассматриваем две случайные величины, которые находятся в стохастической зависимости, то средствами теории информации нельзя установить какая из них является причиной, а какая следствием.